PRAXIS-MAGAZIN Altlasten der Physik (74): Einheit – Gleichheit

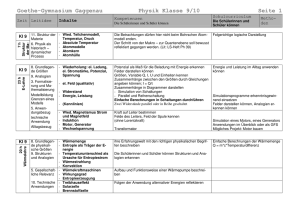
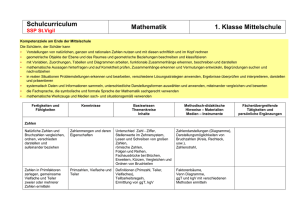
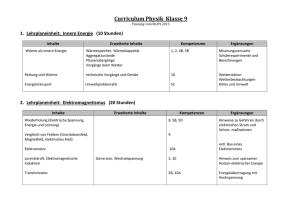
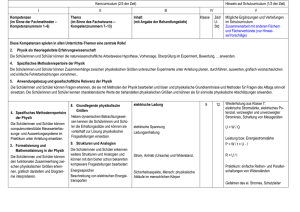
PRAXIS-MAGAZIN
Altlasten der Physik (74):
Einheit – Gleichheit – Vielfachheit
F. Herrmann
Gegenstand
Physikalische Größen, die man nicht aus anderen Größen
ableitet, die so genannten Basisgrößen, werden über eine
Messvorschrift definiert. Das Verfahren besteht aus drei
Teilen:
1. Es wird eine Einheit festgelegt.
2. Es wird erklärt, wie man feststellt, ob die Werte der
Größe an zwei Systemen gleich sind (Gleichheit).
3. Es wird erklärt, was ein Vielfaches oder ein Bruchteil der
Einheit bedeutet (Vielfachheit), siehe etwa [1] oder [2].
Mängel
Wer sich mit dem axiomatischen Aufbau der Physik beschäftigt, mag in dieser Einführung von „Grundgrößen“
eine gewisse Schlüssigkeit und auch Ästhetik sehen. Für
denjenigen, der die Disziplin als Anfänger und Nichtspezialist kennen lernt, ist das Verfahren aber eher unpassend.
Tatsächlich werden Größen in Physikbüchern auch nur selten in aller Strenge nach diesem Verfahren eingeführt.
Überbleibsel des Verfahrens findet man aber noch oft,
manchmal sogar als hervorgehobene Lehrsätze. So wird es
gern in der Mechanik bei der Einführung der Kraft angewendet („Zwei Kräfte sind gleich groß, wenn sie denselben
Körper gleich stark verformen“), und in der Wärmelehre
zur Einführung der Temperaturskala („Der Abstand zwischen Eispunkt und Siedepunkt wird in hundert gleiche
Teile eingeteilt“).
Wir wollen versuchen, die drei Teilschritte in ihrer Bedeutung für den Unterricht zu bewerten.
1. Die Festlegung der Einheit: Dass eine Einheit definiert
sein muss, ist ein Selbstverständlichkeit. Wie sie in den verschiedensten Fällen festgelegt wird, kann für den Berufsphysiker wichtig sein. Trotzdem ist es aber im Wesentlichen eine technische Frage. Das Verfahren muss eine präzise Reproduktion ermöglichen und ist im Allgemeinen
sehr kompliziert. Wenn wir im Unterricht eine Größe neu
einführen und uns um die Bildung einer Anschauung
bemühen, ist seine Kenntnis aber nicht nur nicht hilfreich.
Die Voraussetzungen für ein Verständnis des Verfahrens
sind oft noch nicht vorhanden.
2. Die Erklärung der Gleichheit: Dass sie überhaupt ein
Problem darstellen kann, ist im Anfängerunterricht nur
schwer zu vermitteln. Außerdem würde man sofort sehen,
dass die angeführten Gleichheitserklärungen gar nicht
praktikabel sind. Wenn etwa gesagt wird, zwei Kräfte seien
gleich, wenn sie an einen Körper die gleiche Verformung
verursachen, wie soll man dann die Gleichheit feststellen,
wenn etwa die eine diejenige Kraft ist, die ein Proton auf
ein Elektron ausübt?
3. Die Erklärung der Vielfachen-Bildung scheint der physikalisch wichtigste der drei Schritte zu sein. Sagt er uns
nicht etwas über das Wesen der Größe aus? Wir kennen
46
alle das Problem der Temperaturskala. Definiert man die
Vielfachen über die Ausdehnung des Quecksilbers, so erhält man eine andere Temperaturskala, als wenn man sie
über die Ausdehnung einer anderen Flüssigkeit oder eines
Gases erklärt, und diese ist wieder anders als die thermodynamische Temperaturskala. Tatsächlich ist aber die
Temperaturskala ein Sonderfall. Die Komplikationen, die
hier zunächst aufgetreten waren, existieren längst nicht
mehr. Die Erklärung der Vielfachen einer Einheit ist nämlich in den meisten Fällen trivial. Sie ist trivial für die geometrischen Größen Länge, Flächeninhalt und Volumen,
sowie für die Zeit. Sie ist außerdem trivial für alle extensiven Größen, d. h. Masse, Energie, Impuls, Entropie, elektrische Ladung etc. (das Volumen wurde schon genannt):
Man konstruiert ein Vielfaches des Wertes einer dieser
Größen an einem System S1, indem man eine identische
Kopie S2 des Systems erzeugt und sie mit dem ersten System zu einem neuen System S1,2 zusammenfasst. An S1,2 ist
der Wert aller extensiver Größen doppelt so groß wie an
S1 oder S2. Aus diesen Vielfachendefinitionen folgt aber
auch die aller anderen Größen, die sich als Produkte oder
Quotienten hieraus ergeben, d. h. aller Ströme, intensiven
Größen, Dichten, Stromdichten, Feldstärken usw.
Der einzige Fall, bei dem die Vielfachenbildung problematisch zu sein scheint, wird dann auch in manchen Lehrbüchern, entsprechend ausgewalzt: die Temperaturskala.
Tatsächlich war die Festlegung der Temperaturskala einmal eine Art Schandfleck im Lehrgebäude der Physik: Sie
war abhängig von den speziellen Eigenschaften einer willkürlich gewählten Substanz. Nun ist aber diese Unstimmigkeit längst beseitigt: Die Temperaturskala ist festgelegt
über den Quotienten aus Energie- und Entropieänderung
(als „Energie pro Entropie“):
Ê ∂E(S, V , n,...) ˆ
T =Á
˜¯ ,
Ë
∂S
ähnlich wie die elektrische Spannung über „Energie pro
Ladung“ oder das chemische Potenzial über „Energie pro
Stoffmenge“ definiert ist.
Wir schließen aus all dem, dass das Drei-Schritt-Verfahren
der Definition einer Grundgröße mit keinen besonderen
Einsichten verbunden ist, ja, dass es leicht als Sophisterei
empfunden werden kann.
Es sei nebenbei erwähnt, dass das Verfahren ohnehin nicht
so funktioniert, wie es oft vorgestellt wird. Es wird einem
ja nahegelegt, dass man einen Minimalsatz von Größen
nach dem oben beschriebenen Verfahren definieren muss,
also operational, oder durch Angabe einer Messvorschrift.
Aber das trifft so gar nicht zu, und wird tatsächlich auch
gar nicht immer so gehandhabt. Ein Beispiel ist wieder die
Temperatur: Das Kelvin, also die Einheit der Temperatur,
PdN-PhiS. 4/53. Jg. 2004
PRAXIS-MAGAZIN
ist festgelegt als der 273,16-te Teil des Temperaturintervalls
zwischen dem absoluten Nullpunkt und dem Tripelpunkt
des Wassers. Das Kelvin ist also eine Basiseinheit. Die
Vielfachen der Einheit (die Temperaturskala), sind aber,
wie schon erwähnt wurde, festgelegt über den Quotienten
aus Energie- und Entropieänderung. Die Vielfachenbildung wird also zurückgeführt auf die der extensiven
Größen Energie und Entropie. Die Größe Temperatur erscheint damit als abgeleitete Größe, während ihre Einheit
eine Basiseinheit ist. Um diese Abweichung von der behaupteten Drei-Schritt-Regel zu beseitigen, begibt sich die
Schulphysik manchmal etwas außerhalb der Legalität: Man
erklärt sowohl die Einheit als auch die Vielfachen über die
längst ausgemusterte Quecksilberskala [3].
das Messgerät oder Messverfahren erzeugt. Messverfahren
werden behandelt unabhängig davon, ob eine Größe in
einem gedachten axiomatischen Aufbau als Grundgröße
fungiert oder nicht. Ferner stellt man typische Werte der
Größen an bekannten Systemen vor. Also etwa beim
Druck: der Druck der atmosphärischen Luft, der Druck in
der Wasserleitung, in einem Autoreifen, im Innern der
Erde ...
Man formuliert bei der Kraft keine Lehrsätze über Gleichheit und Vielfachheit. Die Temperaturskala führt man,
analog zur Skala der elektrischen Spannung, ein über Energie pro Entropie.
Entsorgung
Literatur
[1] Götz, R., Dahnke, H., Langensiepen, F. (Hrsg.): Handbuch des Physikunterrichts, Band 1: Mechanik, Aulis Verlag Deubner & Co KG, Köln
1990, S. 51.
[2] Backhaus, U., Schlichting, H. J.: Vom didaktischen Wert physikalischer
Grundgrößen, Physik und Didaktik 3 (1979) 218-225.
[3] Herrmann, F., Job. G.: Altlasten der Physik, Aulis Verlag, Köln 2002,
Vorläufige Temperaturskalen S. 73-74
Man zeigt, wenn immer es möglich ist, wie man eine Größe
messen kann. Dabei ist es nicht unbedingt notwendig, dass
die Funktionsweise des Messgeräts verstanden wird. Es
genügt oft, dass man durch Experimentieren Vertrauen in
Anschrift des Verfassers:
Prof. Dr. Friedrich Herrmann, Abteilung für Didaktik der Physik, Universität, 76128 Karlsruhe
Herkunft
Eine Neigung zu Strenge und Formalisierung an der
falschen Stelle.
PdN-PhiS. 4/53. Jg. 2004
47