Aufgabenblatt Potenzen I - klaus

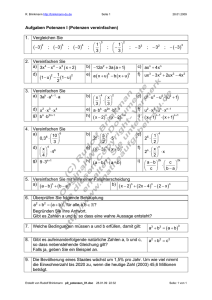
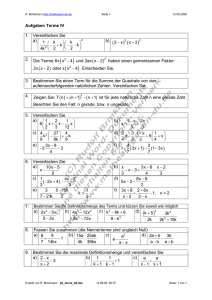
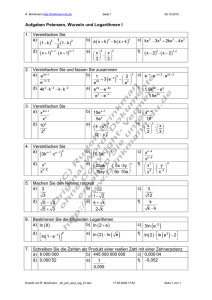
R. Brinkmann http://brinkmann-du.de
Seite 1
08.06.2017
Aufgabenblatt Potenzen I
1. Vergleichen Sie:
 3 
 3 
2
 3 
3
2. Vereinfachen Sie:
a) 3x 4  x 4  x3  x  2 
d) 1  u 
2
1
2
1 u
2
3. Vereinfachen Sie:
a) u3  u4  u5  u2  1


 1
3
 
4
3
 1
 3 


c) axn  4xn
b) x 2  x 3  x 4
c) 3ak  ak 1  a
k
g) u2  x2  un  xn1
h) a  bk  a2n  bk 3
4. Vereinfachen Sie:
6
6  10 
a) 0,3   
 3 
5
b) 2     5
2
4
x x
f)     
3 3
  x  1
n 1
1n
n
x
 1
c) 2   
2
4
5
n
e)  x  3    x  3 
x
f) 2n     x
2
h)  a  b    a  b 
ab  c 
i) 
 

 c  ba
n
2k
9
g) 9  3
2
i)  x  2   x  2
x
n
n 1
3
f) ux3  3x2  2ux3  4x2
k
e)  x  1
4
  3 
 32
e) a  x  u  b  x  u
d) b  b
x
d)    46
4
 33
b) 12a2  3a  a  1
n 1
2n 1
n
2
2k
5. Vereinfachen Sie mit Hilfe einer Fallunterscheidung:
a)  a  b   b  a 
n
n
b)  x  2   2x  4    2  x 
n
n
n
6. Gilt die Behauptung:
a2  b2   a  b  für alle a,b  ?
Begründen Sie Ihre Antwort.
Gibt es Zahlen a und b, sodass eine wahre Aussage entsteht?
2
7. Welche Bedingungen müssen a und b erfüllen, damit gilt:
a3  b3   a  b  ?
3
8. Gibt es aufeinanderfolgende natürliche Zahlen a, b und c, sodass gilt:
a2  b2  c 2
Falls ja, geben Sie ein Beispiel an.
Erstellt von Rudolf Brinkmann 841125126
08.06.17 08:05
Seite: 1 von 1