Potenzen I - Brinkmann.du

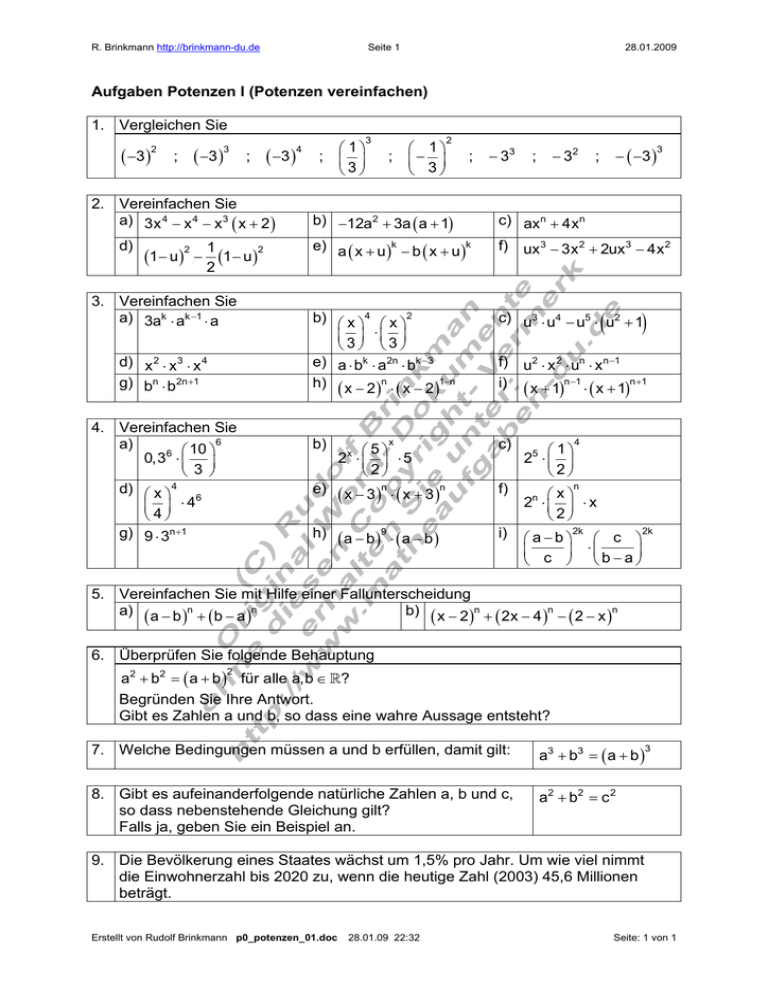
R. Brinkmann http://brinkmann-du.de
Seite 1
28.01.2009
Aufgaben Potenzen I (Potenzen vereinfachen)
1. Vergleichen Sie
( −3 )
2
( −3 )
;
3
;
( −3 )
2. Vereinfachen Sie
a) 3x 4 − x 4 − x 3 ( x + 2 )
d)
(1 − u )
2
−
1
2
(1 − u)
2
3. Vereinfachen Sie
a) 3ak ⋅ ak −1 ⋅ a
d) x 2 ⋅ x 3 ⋅ x 4
g) bn ⋅ b2n +1
4. Vereinfachen Sie
6
a)
6 ⎛ 10 ⎞
0,3 ⋅ ⎜ ⎟
⎝ 3 ⎠
4
d) ⎛ x ⎞
6
⎜ 4⎟ ⋅4
⎝ ⎠
g) 9 ⋅ 3n +1
4
⎛ 1⎞
; ⎜ ⎟
⎝3⎠
3
⎛ 1⎞
; ⎜− ⎟
⎝ 3⎠
2
;
− 33
− 32
;
− ( −3 )
;
3
b) −12a2 + 3a ( a + 1)
c) axn + 4xn
e) a ( x + u )k − b ( x + u )k
f) ux 3 − 3x 2 + 2ux 3 − 4x 2
b) ⎛ x ⎞ 4 ⎛ x ⎞2
⎜ 3 ⎟ ⋅⎜ 3 ⎟
⎝ ⎠ ⎝ ⎠
e) a ⋅ bk ⋅ a2n ⋅ bk − 3
h) ( x − 2 )n ⋅ ( x − 2 )1−n
c) u3 ⋅ u4 − u5 ⋅ u2 + 1
f) u2 ⋅ x 2 ⋅ un ⋅ xn −1
i) ( x + 1)n −1 ⋅ ( x + 1)n +1
b)
⎛5⎞
2 ⋅⎜ ⎟ ⋅5
⎝2⎠
c)
⎛ 1⎞
2 ⋅⎜ ⎟
⎝2⎠
e)
( x − 3) ⋅ ( x + 3)
f)
⎛x⎞
2 ⋅⎜ ⎟ ⋅ x
⎝2⎠
h)
(a − b) ⋅ (a − b)
i)
⎛a−b⎞ ⎛ c ⎞
⎜ c ⎟ ⋅⎜ b − a ⎟
⎝
⎠ ⎝
⎠
x
x
n
9
n
(
)
4
5
n
n
2k
2k
5. Vereinfachen Sie mit Hilfe einer Fallunterscheidung
a) ( a − b )n + ( b − a )n
b) ( x − 2 )n + ( 2x − 4 )n − ( 2 − x )n
6. Überprüfen Sie folgende Behauptung
a2 + b2 = ( a + b ) für alle a,b ∈ \?
2
Begründen Sie Ihre Antwort.
Gibt es Zahlen a und b, so dass eine wahre Aussage entsteht?
7. Welche Bedingungen müssen a und b erfüllen, damit gilt:
a3 + b3 = ( a + b )
8. Gibt es aufeinanderfolgende natürliche Zahlen a, b und c,
so dass nebenstehende Gleichung gilt?
Falls ja, geben Sie ein Beispiel an.
a2 + b2 = c 2
3
9. Die Bevölkerung eines Staates wächst um 1,5% pro Jahr. Um wie viel nimmt
die Einwohnerzahl bis 2020 zu, wenn die heutige Zahl (2003) 45,6 Millionen
beträgt.
Erstellt von Rudolf Brinkmann p0_potenzen_01.doc
28.01.09 22:32
Seite: 1 von 1