Praktikum Messtechnik Vorwort Grundlagen Versuchsaufbau und
Werbung

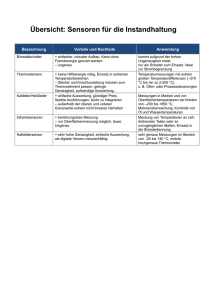
Wintertrimester 2012 P–TM Praktikum Messtechnik Prof. Dr. G. Dollinger Versuch — Temperaturmessung Anleitung Version 2012.1 Vorwort In diesem Praktikumsversuch werden Messungen mit zwei verschiedenen Typen von Berührungsthermometern (Platin-Widerstandsthermometer PT100/1000, Thermoelement) und einem berührungslosen Thermometer (Pyrometer/Infrarot-Thermometer) durchgeführt. Grundlagen Es wird erwartet, dass Sie sich mit den folgenden Grundbegriffen selbständig vertraut machen: Temperaturmessung, Widerstandsthermometer, Pt100, Thermoelement, Pyrometer, Planksches Strahlungsgesetz, Wiensches Strahlungsgesetz, Emissionskoeffizient, Konstantstromquelle. Grundlagen dazu bietet die Vorlesung und Übungen, sowie folgende Literatur • M. Nau, Elektrische Temperaturmessung mit Thermoelementen und Widerstandsthermometern Eigenverlag JUMO Gmbh, FAS146 (2007-01), ISBN-13: 978-3-935742-06-1 Zum freien Download verfügbar unter http://www.jumo.de/de DE/support/faq-weiterbildung/ literatur/themen/temperaturmesstechnik/FAS146.html • Wikipedia mit o.g. Suchbegriffen Versuchsaufbau und Überblick Für den ersten Teil haben Sie verschiedene Typen von Widerstands-Temperatursensoren zur Verfügung, die mit Digitalmultimetern ausgelesen werden. Mit einer Konstantstromquelle (Labornetzgerät bzw. einfache Verstärkerschaltung) werden mit verschiedenen Messleitungsschaltungen der temperturabhängige Widerstand über Strom- und Spannungsmessung gemessen und die Temperatur über die Kennlinientabellen/gleichungen bestimmt (s. Anhang). Als Messobjekte dienen bekannte Temperturfixpunkte z.B der Siedepunkt von Flüssig-Stickstoff (-195,798 ◦ C) oder der Tripelpunkt von Wasser (0.01 ◦ C). Daneben sollen Sie als wichtige Kenngröße den Eigenerwärmungskoeffizient bestimmen. Im zweiten Teil sollen Sie sich mit der Thermoelement-Messtechnik vertraut machen. Dabei wird die Thermoelement-Spannung direkt gemessen und die Temperatur über die Grundwerttabelle (Anhang) bestimmt. Für den letzten Teil steht Ihnen ein Infrarotthermometer zur Verfügung, um sich mit der berührungslosen Temperaturmessung vertraut zu machen. Konkret soll hier exemplarisch der Emissionsgrad eines Objektes bestimmt werden. Konstantstromquelle Eine sehr einfache, günstige und doch genaue Konstantstromquelle kann mittels des Linearreglers LM317 aufgebaut werden (s. Abb.1). >12 V Abbildung 1: Konstantstromquelle mittels Linearregler LM317 Der LM317 ist normalerweise ein Spannungsregler. Er stellt sich so ein, dass zwischen Vout und ADJ 1,25 V liegen. Mit R = U/I kann man leicht errechnen, daß bei einem bestimmten Widerstandswert für den Shunt-Widerstand R1 ein bestimmter Strom fließt. Die Eingangsspannung kann von 4 bis 35 V betrieben werden. Ausgangsspannungen können von 1,25 V bis 36 V ausgegeben werden, die Strombegrenzung arbeitet im Bereich 1250 mA bis 10 mA sehr exakt, darunter ist die Stromstabilisierung für das Praktikum hinreichend genau. Wichtige Hinweise • Sie arbeiten mit Materialien in Temperaturbereichen mit Verletzungsgefahr (fl. Stickstoff - kochendes Wasser - Schmelzpunkt von Metallen)! Der Umgang erfordert Sorgfalt und Vorsicht sowie das Tragen von Schutzbrille und Schutzhandschuhen zu Ihrer eigenen Sicherheit. • Achten Sie IMMER auf korrekten Anschluss der Multimeter, fragen Sie bei Zweifel Ihren Betreuer. Insbesondere bei der Stromeinstellung der Konstantstromquelle stellen sie bitte sicher, dass Sie das Multimeter nicht überlasten (Imax = 500 mA) und stellen es zuerst auf den 10A-Eingang! ACHTUNG: Das Vorschaltkästchen mit Stromregler zur Einstellung kleiner Ströme im mA-Bereich ist nicht linear und kann im Anschlag auch Ströme > 500 mA liefern! • Zur Ermittlung der Messunsicherheiten der Multimeter (s. techn. Daten im Anhang): Nehmen Sie einen Gerätefehler wie im Prozentwert angegeben an (z. B. 0.025 % vom Messwert der Spannung), jedoch für den Digitalisierungsfehler jeweils nur 1 dgt (= ˆ letzte Stelle der Anzeige). Aufgabenstellung 1. Widerstandsthermometer (a) Vorbereitung Bereiten Sie nach Anweisung des Betreuers im Dewar (Isoliergefäß) Eiswasser vor, um ein homogenes Temperturgleichgewicht möglichst nahe am Tripelpunkt des Wassers zu erhalten. (b) Abgleich Zweileiterschaltung Hier soll ein PT100-Fühler in Zweileiterschaltung abgeglichen werden, d.h. die parasitären Leitungswiderstände bestimmt werden. Mit diesen sollen Sie in der Ausarbeitung berechnen, welcher Korrekturwert in der Temperaturbestimmung durch diese Widerstände nötig wird. • Finden Sie zunächst durch Messung mit dem Multimeter (Einstellung Ω) heraus, wie die vier Leitungen an den PT100-Fühler angeschlossen sind. • Zeichnen Sie ein Schaltbild mit allen Widerständen in Protokollbuch und bestimmen Sie die parasitären Leitungswiderstände. Verwenden Sie hierzu das ROTE Multimeter als Ohm-Meter. Für die Ausarbeitung benötigen Sie alle Messunsicherheiten der Geräte. Notieren Sie diese! Aufgaben zur Ausarbeitung: i. Erstellen Sie zunächst eine knappe Versuchsbeschreibung mit sauberer Skizze des Messaufbaus, Ziel des Versuchs, Erklärung der Messgrößen und der auftretenden Messunsicherheiten. ii. Wie groß ist der gesamte parasitäre Leitungswiderstand in Zweileiterschaltung? Berechnen Sie die gesamte Messunsicherheit. iii. Schätzen Sie anhand der Kennlinientabelle im Anhang ab, welche Abweichung ∆TL Sie in der Temperaturbestimmung machen würden, wenn Sie die Zuleitungswiderstände nicht berücksichtigen. iv. Welche gesamte Messunsicherheit erhalten Sie für die Temperaturbestimmung bei Raumtemperatur? (c) Messung in Vierleiterschaltung Hier soll in Vierleiterschaltung 3 verschiedene Temperaturmesspunkte ermittelt werden. Entscheidend sind jedoch nicht unbedingt die ermittelten Werte an sich, sondern die Angabe der Messunsicherheit dazu! Schließen Sie zunächst den PT100 an das Vorschaltkästchen (Konstantstromquelle) in Vierleiterschaltung an - Überprüfung der Schaltung durch den Betreuer!. Stellen Sie einen Strom < 4 mA ein. Messen Sie nach Erreichen des Temperaturgleichgewichts Strom und Spannung (Messbereiche für Multimeter: mA und mV) für: • Raumtemperatur (Wärmekontakt mit Metallblock o.ä. über Leitpaste) • Tripelpunkt des Wassers (Eiswasser im Dewar-Gefäß) • Siedepunkt von Stickstoff (flüssiger Stickstoff in Isolierkanne) Für die Ausarbeitung benötigen Sie alle Messunsicherheiten (Geräte/Digitalisierungsfehler s. Hinweis oben). Notieren Sie die Messunsicherheiten für Strom und Spannungsmessung! Aufgaben zur Ausarbeitung: i. Erstellen Sie zunächst wieder eine knappe Versuchsbeschreibung mit sauberer Skizze des Messaufbaus, Ziel des Versuchs, Erklärung der Messgrößen und der auftretenden Messunsicherheiten. Warum messen Sie nicht direkt den Widerstand, sondern Strom und Spannung? ii. Erstellen und Berechnen Sie eine Messwert-Tabelle (z.B. Excel) mit folgenden Spalten: • Strom I ± δI • Spannung U ± δI • Widerstand R = U/I • Unsicherheit δR • Temperatur ϑtab über Interpolation der Werte in der Kennlinientabelle • Temperatur ϑinv über Anwendung der inversen Kennline von Gl. 6 • Gesamte Messunsicherheit δϑ Die Berechnung der Werte ist in der Ausarbeitung zu dokumentieren! iii. Geben Sie die ermittelten Temperaturmesswerte mit gesamter Messunsicherheit mit SINNVOLLER Stellenangabe an (s. Richtlinien zur Praktikumsausarbeitung). iv. Diskutieren Sie die Ergebnisse kurz! (d) Eigenerwärmungskoeffizient Der Eigenerwärmungskoeffizient K ist die Zunahme der gemessenen Temperatur ∆T pro Wärmeleistung ∆P , die in den Fühler eingetragen wird. Er ist von Fühlerkonstruktion sowie der zu messenden Umgebung abhängig. Im Folgenden sollen Sie K für den vorliegenden PT100 in einer der Umgebungen Eiswasser oder fl. Stickstoff in reiner Konvektion (v = 0) bestimmen. Messen Sie dazu in Vierleiterschaltung Strom und Spannung für eine Messreihe mit etwa 10 Strom-Werten vom minimal einstellbaren Strom (>0,5 mA) bis etwa I = 50 mA (sinnvolle Einteilung, d.h. größer werdende Abstände bei hohen Strömen!). Falls die Spannung größer 12 V wird, benutzen Sie das Labornetzgerät direkt als Stromquelle (Die Verstärkerbox kann nicht mehr Spannung liefern!!!). Notieren Sie dies in der Messwert-Tabelle in einer Spalte ”Bemerkungen”. Achtung: Ab etwa I ≥ 20 mA sollten Sie den Temperaturausgleich abwarten, bis 2 oder 3 signifikante Stellen am Multimeter etwa stabil bleiben (nach Hinweis des Betreuers). Aufgaben zur Ausarbeitung: i. Erstellen Sie wieder eine knappe Versuchsbeschreibung mit sauberer Skizze des Messaufbaus, Ziel des Versuchs, Erklärung der Messgrößen und der auftretenden Messunsicherheiten. ii. Erstellen Sie wieder eine (Excel)Tabelle (I ±δI, U ±δU , R±δR, P ±δP , ϑ±δϑ). Berechnen Sie in der Tabelle die Leistung P und Temperatur ϑ (Tabelleninterpolation oder inverse Kennlinie von Gl. 6). iii. Tragen Sie in einem Diagramm ϑ als Funktion von P auf (mit Fehlerbalken!) und ermitteln Sie K graphisch mit Unsicherheit δK. iv. Wie groß ist also die Temperaturzunahme bei der Messung in der vorigen Aufgabe (Eiswasser oder fl. Stichstoff)? 2. Thermoelement Im Folgenden sollen mit einem Typ-K-Thermoelement die Temperatur von Eiswasser und fl. Stickstoff gemessen werden. Ziel ist wieder vielmehr die Bestimmung der Messunsicherheit im Vergleich zur Messung mit einem Pt100-Fühler. (a) Vergleichstemperatur und Grundwertetabelle Die Thermospannung bildet sich immer durch eine Temperaturdifferenz von Messund Vergleichsstelle aus. Vergleichsstelle ist der Übergang der Messleitung in das Multimeter. Verwenden Sie daher in der Ausarbeitung als Vergleichstemperatur den zuvor ermittelten Wert der Raumtemperatur. • Messen Sie für das vorliegende Typ-K Thermoelement die Thermospannung U ± δU mit dem Multimeter am Tripelpunkt von Wasser (Eiswasser). • Überprüfen Sie die Ausgabe des Multimeters im Temperatur-Modus ( ◦ C). Geben Sie auch hier die Messunsicherheit an (aus dem Datenblatt des Multimeters). • Messen Sie die Thermospannung von Flüssig-Stickstoff. Welchen Temperaturwert zeigt das Multimeter im Temperatur-Modus ( ◦ C) an? Aufgaben zur Ausarbeitung: i. Erstellen Sie wieder eine knappe Versuchsbeschreibung mit sauberer Skizze des Messaufbaus, Ziel des Versuchs, Erklärung der Messgrößen und der auftretenden Messunsicherheiten. ii. Berechnen Sie aus den gemessenen Thermospannungen über die Grundwertetabellen des Typ-K-Fühlers (Gegeben für eine Vergleichstemperatur von 0 ◦ C!) die Temperatur des Tripelpunktes ϑTP ± δϑTP bzw. des Siedepunktes von Stickstoff ϑLN ± δϑLN . Interpolieren Sie ggf. die Tabellenwerte. Berücksichtigen Sie bei der Fehlerrechnung auch die Messunsicherheit in der Raumtemperatur-Bestimmung von oben! iii. Diskutieren Sie die Messunsicherheit im Vergleich zur Messung mit dem Pt100. Welche Messung ist genauer? iv. Diskutieren Sie Abweichungen des Multimeters im Temperatur-Modus ( ◦ C) unter Berücksichtigung der Messunsicherheiten. (b) Siedepunkt des Wassers Bringen Sie mit der Herdplatte das Wasser zum kochen. Sie sollen nun mit dem Thermoelement die Siedetemperatur des Wassers bestimmen. Messen Sie dazu die Thermospannung Aufgaben zur Ausarbeitung: i. Bestimmen Sie die Temperatur mit Messunsicherheit. ii. Ist das Ergebnis im Einklang mit der erwarteten Siedetemperatur? Diskutieren Sie das Ergebnis und mögliche Fehlerquellen! 3. Infrarotthermometer Sie erhalten vom Betreuer ein Infrarot-Thermometer. Dieses misst die spektrale Strahldichte L(λ, T ) eines Gegenstandes der Temperatur T in einem Wellenlängenbereich von 8 − 14 µm. Das Plancksche Strahlungsgesetz gibt die Strahldichte für einen idealen schwarzen Körper an. Die spektrale Ausstrahlung eines realen Körpers weicht allerdings meist von der eines schwarzen Strahlers ab, d.h. die meisten Gegenstände emittieren wellenlängen- und auch temperaturabhängig. Diese Abhängigkeit wird über den Emissionsgrad ε(λ, T ) erfasst mit L(λ, T ) (1) ε(λ, T ) = LS (λ, T ) Im Folgenden sollen Sie den Emissionsgrad eines Gegenstandes bestimmen. Hinweis: Der Laser hat rein gar nichts mit der Temperaturmessung zu tun, sondern ist nur als grobe Zieleinrichtung eingebaut! NIEMALS in die Optiken fassen und nicht in den Laserstrahl blicken! Das FLUKE-Thermometer ist mit besonderer Sorgfalt zu behandeln. • Deaktivieren Sie die Emissionsgrad-Korrektur des Gerätes. Stellen Sie dazu nach Anleitung des Betreuers den Emissionsgrad auf ε = 1 • Heizen Sie mit der Herdplatte einen eloxierten Alu-Zylinder auf eine Temperatur von ca. 300 ◦ C (Vorsicht Verbrennungsgefahr!). Bestimmen Sie die tatsächliche Temperatur Tist des Gegenstandes mit dem Thermoelement (Spannungsmessung) oder PT100 (Vierleiter-Schaltung). Achten Sie auf guten Wärmekontakt (Leitpaste!) und lassen Sie den Gegenstand ins Gleichgewicht kommen • Messen Sie die Temperatur Tpyr mit dem Pyrometer möglichst in der Nähe der Vergleichsstelle (Messfeld-Durchmesser beachten!) und zeitnah zur Vergleichstemperturmessung. Aufgabe zur Ausarbeitung: Bestimmen Sie in der Ausarbeitung über die gemessenen Temperaturen Tist und Tpyr den Emissionsgrad (hier ausnahmsweise ohne Unsicherheit). Zur Integration der spektralen Strahldichte im Messbbereich der Geräte von λ = 8 . . . 14 µm können Sie die Wiensche Näherung anstelle der Planckschen Strahlungsformel verwenden (Die Wiensche Näherung ist im Bereich kleiner Wellenlängen und Temperaturen λT ≪ hc/k = 14404 µm K eine gute Näherung). Hinweis zur Integration: ∫ 3 2 2 3 1 −a − a a + 3a x + 6ax + 6x x = e x e λ5 a4 x3 Anhang Kennlinie und inverse Kennline PT100 Im Bereich von 0 ◦ C ≤ ϑ ≤ 850 ◦ C wird die Kennlinie als Polynom 2. Grades angegeben: ( R(ϑ) = R0 1 + A·ϑ + B ·ϑ2 ) . (2) Für −200 ◦ C ≤ ϑ ≤ 0 ◦ C gilt ein Polynom 4. Grades: ( [ R(ϑ) = R0 1 + A·ϑ + B ·ϑ2 + C ϑ − 100 ◦ C]·ϑ3 ]) . (3) Die Koeffizienten A, B und C sind nach der (neuen) DIN IEC 751 (ITS-90) industieller PTMesswiderstände festgelegt mit: A = +3.9083·10−3 ◦ C−1 B = −5.775·10−7 ◦ C−2 C = −4.183·10−12 ◦ C−4 (4) Die inverse Kennlinie lautet damit für ϑ ≥ 0 ◦ C A ϑ(R) = − − 2B √ A2 1 + 2 4B B ( R −1 100 Ω ) . (5) Für den gesamten Temperaturbereich kann die Kennlinie numerisch invertiert werden. In einem digitlen Temperaturmessgerät wird üblicherweise die folgende Approximationsgleichung für die inverse Kennlinie verwendet werden: ( ϑ(R) = K mit 6060.52·R − 245.668 2566.96 Ω − R K = 1 ◦C K = 0.998291 ◦ C ) für T ≥ 0 ◦ C für T < 0 ◦ C (6) (7) Grundwert-Tabelle für Termoelement Richtlinien zur Praktikums–Ausarbeitung Eine Ausarbeitung muss für fachkundige Außenstehende ohne Kenntnis der Aufgabenstellung oder dieser Anleitung nachvollziehbar sein, ohne große Suche nach Messwerten im Protokoll. D.h. zu jedem Aufgabenteil gehört: • Überschrift mit Fach/Thema/Datum/Ort (auch das Protokoll muss Datum und korrekterweise auch Uhrzeit habe!!!) • Knappe Versuchtsbeschreibung (wenige Zeilen) mit Sinn und Ziel der Aufgabe. Es kann auch auf Details in der Anleitung verwiesen werden! • Einführung/Definition der benutzten Messgrößen. • Rechnungen mit allen notwendigen Zwischenschritten. Einsetzen der Zahlenwerte in die End-Formel hinschreiben (nicht nur das TaschenrechnerErgebnis). • Angabe der Messergebnisse und Messunsicherheiten zu jeder Größe mit sinnvoller Angabe von Stellen. Messgrößen werden mit gleichen Stellen wie die Unsicherheit (mathematisch) gerundet, die Unsicherheit wird auf die erste zählende Ziffer (erste Ziffer von links ungleich Null) AUFgerundet - Ausnahme bei Ziffer 1 oder 2, dann wird auf ZWEI zählende Ziffern AUFgerundet! Ist noch keine Unsicherheit berechnet, kann der Wert mit 5 zählende Ziffern gerundet notiert werden (Genauigkeit von 10−5 wird hier im Praktikum auf jeden Fall nicht übertroffen). • Angabe des Ergebnisses mit Unsicherheit, also z. B. U = (2.500 ± 0.012) mV • Verweise auf Bilder und Tabellen auf anderen Seiten (Seitenzahlen) • Tabellen und Zeichnungen aus dem Protokoll sollten nochmal sauber in die Ausarbeitung übernommen werden, wenn im Protokoll nur groß und unleserlich ausgeführt wurden. Insbesondere gehören auch Messunsicherheiten in Tabellen, wenn Sie sich von Wert zu Wert ändert, ansonsten kann man Gänsefüßchen o.ä. verwenden. • Vergleich des Ergebnisses mit Literatur oder erwartetem Wert. Liegt der erwartete Wert innerhalb des Fehlerintervalls? Welche Messgröße/Welcher Messfehler trägt am meisten zur Unsicherheit bei? • Diskussion der möglichen Gründe, wenn der Wert außerhalb des Fehlerinterwals abweicht (Systematische Fehler, ungeeigneter Messaufbau), aber pauschale Aussagen reichen nicht. Qualitative Aussagen (zu wenig, viel zu hoch, etwas zu hoch...) nützen niemand, wenn sie nicht durch Vergleich von Zahlenwerten untermauert sind! • Ergebnis des Versuchs 1