Name: (Nr. ) 3. Klassenarbeit

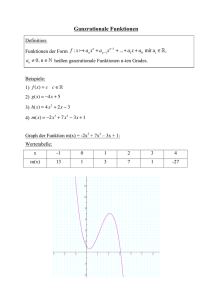
Mathemat ik 11b
3. Klassenarbeit
Thema: Funktionen, Nullstellen und Grenzverhalten
Name: <KLASSE_11B>
(Nr. <NR.>)
19. Januar 2001
e-mail:
0. Für saubere und übersichtliche Darstellung, klar ersichtliche Rechenwege, Antworten in ganzen
Sätzen und Zeichnungen mit spitzem Bleistift erhältst du bis zu 3 Punkte.
Punkte
/3
1. In einer Studie wurden Prognosen über die
mögliche Entwicklung der Chromvorräte auf der
Welt veröffentlicht. In einem Szenario wurde
eine jährliche Steigerung der Nutzungsrate um
2,6 % zu Grunde gelegt.
Welches der neben stehenden vier Schau- bilder
(A, B, C oder D) entspricht dem Szenario?
Begründe deine Wahl!
/4
2. Gib je eine Funktion an, die der Gesamtlänge
aller Kanten eines Würfels den Oberflächeninhalt O bzw. den Rauminhalt V zuordnet.
/4
3. Untersuche die Funktion f(x) = x 3 − x + 1 auf Symmetrie zur y-Achse oder zum Ursprung.
/4
4. Bestimme alle Nullstellen der Funktion f(x) = 2x 4 + 6x 3 − 12x − 8.
/7
5. Untersuche das Grenzverhalten der Funktion
g(x) = 4x
x 2 für x t ! º .
/4
6. Die nebenstehende Abbildung zeigt das
Schaubild einer Funktion f(x). Wähle aus der
folgenden
Liste
die
zugehörige
Funktionsvorschrift aus und begründe deine
Wahl.
a) f(x) = (x − 1)(x − 3)
b) f(x) =
1
(x−2)
c) f(x) =
2
(x−2)2 − 2
(x−1)(x−3)
(x−2)
x−2
(x−1)(x−3) − 2
d) f(x) =
e) f(x) =
/4
JOKER: Verwende möglichst wenige der folgenden Zahlen 2, 3, 5, 6, 8, 9 höchstens einmal, um mit
Hilfe der vier Grundrechenarten und eventuell Klammern die Zahl 554 (!2) in einem Term zu
berechnen.
Viel Spaß und viel Erfolg!
Punkte:
(von 30)
Schnitt:
Note:
Standardabweichung:
Median:
Rückgabe 2001-01-22
/3
Mathemat ik 11b
19. Januar 2001
Erwartungshorizont
1. Das einzig mögliche der vier angebotenen Schaubilder ist D, denn der Abbau der Vorräte nimmt
jährlich konstant zu. Es muss sich also um eine parabelförmig nach unten führende Kurve handeln.
2. Der Oberflächeninhalt eines Würfels besteht aus 6 Quadraten und 12 gleich langen Kanten.
g
1
Deshalb gilt: O(g) = 6 $ ( 12 ) 2 = 24 g 2
mit g = Gesamtlänge der Kanten
g 3
1
3
sowie
V(g) = ( 12 ) = 1728 g
3. Wäre f(x) achsensymmetrisch zur y-Achse, so müsste gelten f(x) = f(−x)
f(−x) = (− x) 3 − (− x) + 1 = −x3 − x + 1 ! f(x)
Wäre f(x) punktsymmetrisch zum Ursprung, so müsste gelten f(x) = −f(−x)
−f(−x) = −(−x 3 − x + 1) = x 3 + x − 1 ! f(x)
Also ist f(x) weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
4. Zunächst bestimmt man eine Nullstelle durch Raten (evtl. Teiler des absoluten Gliedes):
f(−1) = 2 $ (−1) 4 + 6 $ (−1) 3 − 12 $ (−1) − 8 = 2 − 6 + 12 − 8 = 0
Also dividiert man (für x ! −1) durch (x + 1)
(2x 4 + 6x 3 − 12x − 8) : (x + 1) = 2x 3 + 4x 2 − 4x − 8
−(2x 4 + 2x 3 )
(4x 3 − 12x − 8 )
Eine weitere Nullstelle ist −2, denn
3
2
−(4x + 4x )
f(−2) = 2 $ (−2) 4 + 6 $ (−2) 3 − 12 $ (−2) − 8
(−4x 2 − 12x − 8 )
= 32 − 48 + 24 − 8 = 0
2
(
)
− −4x − 4x
Noch eine Polynomdivision liefert:
(−8x − 8)
−(−8x − 8 )
(2x 3 + 4x 2 − 4x − 8) : (x + 2) = 2x 2 − 4
0J
Der Term 2x 2 − 4 = 2(x 2 − 2 ) = 2(x − 2 )(x + 2 ) hat die Nullstellen ! 2 .
Also hat f(x) die Nullstellen −1, − 2, 2 und − 2 .
5. g(x) =
4x
x2
=
also gilt xd+º
lim g(x) =xd−º
lim g(x) = 0
4
x
6. Es muss sich um die unter c) vorgeschlagene Funktion
f(x) = (x−2)2 − 2 handeln,
da f(x) die waagerechte Asymptote y = −2 und die senkrechte Asymptote x = 2 besitzt.
Die erkennbaren Nullstellen x 1 = 1 und x 2 = 3 werden auch bestätigt, denn
2
f(x) =
2−2(x−2) 2
(x−2)2
=
2−2(x 2 −4x+4)
(x−2) 2
=
−2(x 2 −4x+3)
(x−2) 2
JOKER:
JOKE :
3 Punkte für: 554 = (3 + 2) $ 8 $ (9 + 5 ) − 6
2 Punkte für 553 = [(8 + 2) $ 9 + 3] $ 6 − 5
555 = (6 $ 2 $ 9 + 3) $ 5
1 Punkt für
552 = [(5 + 2) $ 9 + 6] $ 8
556 = (6 $ 5 $ 9 + 8) $ 2
=
−2(x−1)(x−3)
(x−2) 2