Wiederholung ganzrationale Funktionen

Wiederholung ganzrationale Funktionen
Aufgaben:
1.0 Gegeben ist die Funktion f (x) = x 3 − 2x 2 + x mit D f = ! .
1.1 Bestimmen Sie die Anzahl, Lage und Vielfachheit der Nullstellen der Funktion f.
1.2 Untersuchen Sie das Symmetrieverhalten der Funktion f.
1.3 Untersuchen Sie das Verhalten der Funktionswerte der Funktion f für x → ±∞ .
1.4 Skizzieren Sie den grundsätzlichen Verlauf des Graphen Gf der Funktion f.
2.0 Gegeben ist die Funktion f (x) = x 4 − x 2 − 12 mit D f = ! .
2.1 Bestimmen Sie die Anzahl, Lage und Vielfachheit der Nullstellen der Funktion f.
2.2 Untersuchen Sie das Symmetrieverhalten der Funktion f.
2.3 Untersuchen Sie das Verhalten der Funktionswerte der Funktion f für x → ±∞ .
2.4 Skizzieren Sie den grundsätzlichen Verlauf des Graphen Gf der Funktion f.
3.0 Gegeben ist die Funktion f (x) = x 3 − 3x 2 − 6x + 8 mit D f = ! .
3.1 Bestimmen Sie die Anzahl, Lage und Vielfachheit der Nullstellen der Funktion f.
3.2 Untersuchen Sie das Symmetrieverhalten der Funktion f.
3.3 Untersuchen Sie das Verhalten der Funktionswerte der Funktion f für x → ±∞ .
3.4 Skizzieren Sie den grundsätzlichen Verlauf des Graphen Gf der Funktion f.
4.0 Gegeben sind die reellen Funktionen h t : x !
mit D h t = ! und t ∈! . (Abitur 2016 AI)
1
x(tx − 1)(x + 4)(x − 3)
4
4.1 Bestimmen Sie Anzahl, Lage und Vielfachheit der Nullstellen der Funktion ht in
Abhängigkeit von t.
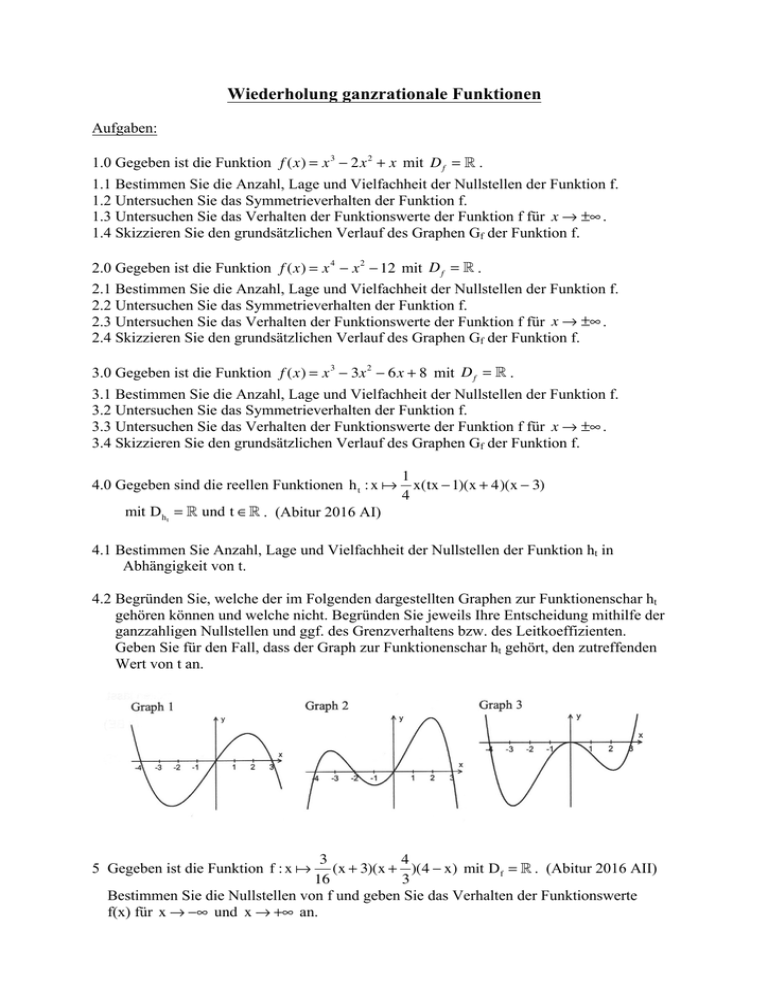
4.2 Begründen Sie, welche der im Folgenden dargestellten Graphen zur Funktionenschar ht
gehören können und welche nicht. Begründen Sie jeweils Ihre Entscheidung mithilfe der
ganzzahligen Nullstellen und ggf. des Grenzverhaltens bzw. des Leitkoeffizienten.
Geben Sie für den Fall, dass der Graph zur Funktionenschar ht gehört, den zutreffenden
Wert von t an.
3
4
(x + 3)(x + )(4 − x) mit D f = " . (Abitur 2016 AII)
16
3
Bestimmen Sie die Nullstellen von f und geben Sie das Verhalten der Funktionswerte
f(x) für x → −∞ und x → +∞ an.
5 Gegeben ist die Funktion f : x !
6.0 Gegeben ist die Funktionenschar g a : x ! 0,25(x 3 − 2ax 2 ) mit x,a ∈" .
(Abitur 2016 AII)
6.1 Ermitteln Sie die Nullstellen von ga und geben Sie deren Vielfachheit in Abhängigkeit
von a an.
Nun wird a = 3 gesetzt und es gilt: g 3 (x) = 0,25(x 3 − 6x 2 ) . Des Weiteren ist die
lineare Funktion t : x ! −3x + 2 mit x ∈" gegeben.
6.2 Untersuchen Sie rechnerisch, ob die abschnittsweise definierte Funktion
⎧⎪ g 3 (x)
für x ≤ 2
h :x ! ⎨
an der Nahtstelle stetig ist.
für x > 2
⎪⎩ t(x)
Lösungen:
1.1 Ansatz: x 3 − 2x 2 + x = 0
⇒ x(x 2 − 2x + 1) = 0 ⇒ x1 = 0
⇒ x 2 − 2x + 1 = 0 ⇒ (x − 1)2 = 0 ⇒ x2 = 1
⇒ f hat zwei Nullstellen bei x1 = 0 (einfach) und bei x 2 = 1 (doppelt)
⎧ f (x)
1.2 f (−x) = (−x)3 − 2(−x)2 + (−x) = −x 3 − 2x 2 − x ≠ ⎨
⎩− f (x)
⇒ G f ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
Alternative:
G f ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung, weil
im Funktionsterm gerade und ungerade Exponenten auftreten.
1.3 lim (x 3 − 2x 2 + x) existiert nicht
x→∞
lim (x 3 − 2x 2 + x) existiert nicht
x→−∞
1.4
f (x) → ∞ für x → ∞
f (x) → −∞ für x → −∞
2.1 Ansatz: x 4 − x 2 − 12 = 0
Substitution: z = x 2
⇒ z 2 − z − 12 = 0 ⇒ (z + 3)(z − 4) = 0 ⇒ z1 = −3 z2 = 4
Resubstitution:
1) x 2 = −3 ( f )
2) x 2 = 4 ⇒ x1 = −2 x2 = 2
⇒ f hat zwei Nullstellen bei x1 = -2 (einfach) und bei x 2 = 2 (einfach)
2.2 f (−x) = (−x)4 − (−x)2 − 12 = x 4 − x 2 − 12 = f (x)
⇒ G f ist achsensymmetrisch zur y-Achse.
Alternative:
G f ist achsensymmetrisch zur y-Achse , weil im Funktionsterm
nur gerade Exponenten auftreten.
2.3 lim (x 4 − x 2 − 12) existiert nicht
x→∞
lim (x 4 − x 2 − 12) existiert nicht
x→−∞
2.4
f (x) → ∞ für x → ∞
f (x) → ∞ für x → −∞
3.1 Ansatz: x 3 − 3x 2 − 6x + 8 = 0 Ausprobieren: x1 = 1
Polynomdivision:
(x 3 − 3x 2 − 6x + 8) : (x − 1) = x 2 − 2x − 8
− (x 3 − x 2 )
−2x 2 − 6x + 8
− (−2x 2 + 2x)
−8x + 8
− (−8x + 8)
− − − − −
Weitere Nullstellen: x 2 − 2x − 8 = 0 ⇒ (x − 4)(x + 2) = 0 ⇒ x2 = 4 x3 = −2
⇒ f hat drei Nullstellen bei x1 = 1 (einfach), bei x 2 = 4 (einfach)
und bei x 3 = -2 (einfach)
⎧ f (x)
3.2 f (−x) = (−x)3 − 3(−x)2 − (−6x) + 8 = −x 3 − 3x 2 + 6x + 8 ≠ ⎨
⎩− f (x)
⇒ G f ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
Alternative:
G f ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung, weil
im Funktionsterm gerade und ungerade Exponenten auftreten.
3.3 lim (x 3 − 3x 2 − 6x + 8) existiert nicht
x→∞
lim (x 3 − 3x 2 − 6x + 8) existiert nicht
x→−∞
3.4
f (x) → ∞ für x → ∞
f (x) → −∞ für x → −∞
4.1
1
x(tx − 1)(x + 4)(x − 3) = 0
4
1
⇒ x1 = 0 x 2 =
x 3 = −4 x 4 = 3
t
t = 0 : h 0 hat drei Nullstellen bei x1 = 0, x 2 = −4 und x 3 = 3
t = −0,25 : h −0,25 hat drei Nullstellen bei x1 = 0, x 2 = −4 und x 3 = 3
t=
1
: h 1 hat drei Nullstellen bei x1 = 0, x 2 = −4 und x 3 = 3
3 3
1⎫
1
⎧
t ∈! \ ⎨−0,25;0; ⎬ : h t hat vier Nullstellen bei x1 = 0, x 2 = , x 3 = −4 und x 4 = 3
3⎭
t
⎩
4.2
Graph 1 kann zur Funktionenschar h t gehören mit t = 0
1
⇒ h 0 (x) = − x(x + 4)(x − 3)
4
Hoch drei Funktion mit negativem Leitkoeffizienten (kommt von oben, geht nach unten)
Graph 2 kann zur Funktionenschar h t gehören mit t = -0,5
Hoch vier Funktion mit negativem Leitkoeffizienten (kommt von unten, geht nach unten)
Graph 3 kann nicht zur Funktionenschar h t gehören, weil es bei Null
nie eine doppelte Nullstelle geben kann.
5
3
4
(x + 3)(x + )(4 − x) = 0
16
3
4
⇒ x1 = −3 x 2 = −
x3 = 4
3
4
⎡3
⎤
lim ⎢ (x + 3)(x + )(4 − x) ⎥ existiert nicht
x→−∞ ⎣ 16
3
⎦
4
⎡3
⎤
lim ⎢ (x + 3)(x + )(4 − x) ⎥ existiert nicht
x→∞ ⎣ 16
3
⎦
f(x) → +∞ für x → −∞
f(x) → −∞ für x → +∞
6.1
0,25(x 3 − 2ax 2 ) = 0 ⇒ x 3 − 2ax 2 = 0 ⇒ x 2 (x − 2a) = 0
⇒ x1 = 0 x 2 = 2a
a = 0 : eine Nullstelle bei x = 0 (dreifach)
a ∈! \ {0} : zwei Nullstellen bei x1 = 0 (doppelt) und bei x 2 = 2a (einfach)
6.2
Stetigkeit :
⎡⎣ 0,25(x 3 − 6x 2 ) ⎤⎦ = −4
lim
<
x→ 2
lim
[ −3x + 2 ] = −4
>
x→ 2
h(2) = 0,25(2 3 − 6 ⋅ 2 2 ) = −4
⇒ h stetig bei x = 2