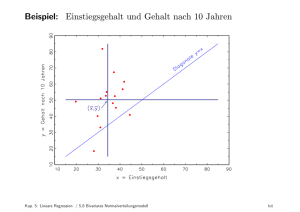
14 Regression, lineare Korrelation und Hypothesen

14
Regression, lineare Korrelation und
Hypothesen-Testverfahren
14.1 Regressionsverfahren
In der Meßtechnik kommt es häufig vor, daß eine Schar von aufgenommenen
Meßpunkten durch eine geeignete analytische Funktion in Form einer Anpaßkurve beschrieben werden soll.
Im folgenden gehen wir davon aus, daß n Messungen durchgeführt werden, welche die Wertepaare {xi , yi }(i = 1, 2, . . . , n) liefern. Anschließend wird
an diese Meßwerte eine Kurve ỹ(x) angepaßt. Daraus ergeben sich die Abweichungen Δi zwischen den einzelnen Meßpunkten und der Anpaßkurve im
jeweiligen Meßpunkt xi zu
Δi = ỹ(xi ) − yi .
(14.1)
Dabei wird x als unabhängige (vorgebbare) Variable und y als abhängige
Variable bezeichnet.
Der Ansatz der minimalen Fehlerquadrate gemäß dem sog. Gaußschen
Minimalprinzip [69] (Gaußsches Prinzip der kleinsten Quadrate) ergibt
Δ=
n
i=1
Δ2i =
n
!
[ỹ(xi ) − yi ]2 =
min. .
(14.2)
i=1
In Gleichung (14.2) ist als unbekannte Funktion die Anpaßkurve ỹ(x) enthalten. Die beschriebene Fehlerquadratsumme Δ hängt nun von der Wahl dieser
Anpaßkurve ab. Die Festlegung der diese Anpaßkurve beschreibenden analytischen Funktion und die anschließende Berechnung ihrer Koeffizienten (s.u.)
wird als Regressionsverfahren bezeichnet. Falls Proportionalität zwischen der
abhängigen und unabhängigen Variablen herrscht, läßt sich in diesem Fall die
Schar vom Meßwerten durch eine Gerade beschreiben. Man spricht dann von
einer Ausgleichsgeraden, die durch sog. lineare Regression bestimmt wird.
434
14 Regression, lineare Korrelation und Hypothesen-Testverfahren
14.1.1 Ausgleichsgerade (lineare Regression)
Die lineare Regression ist die für die ingenieurmäßige Praxis wichtigste Form
der Regressionsanalyse. Sie hat das Ziel, durch eine Schar von (in aller Regel) experimentell bestimmten Wertepaaren {xi , yi } eine Ausgleichsgerade zu
legen. Dabei wird x als unabhägige und y als abhängige Variable betrachtet.
Die Ausgleichsgerade bestimmt letztlich die nach dem Gaußschen Minimalprinzip beste lineare Approximation der Funktion y(x), die hier von diskreten
Wertetupeln repräsentiert wird.
Im folgenden gehen wir davon aus, daß n Meßwerte {xi , yi }(i = 1, 2, . . . , n)
vorliegen. An diese Meßwerte soll eine Gerade der Form ỹ(x) = mx + b angepaßt werden (Abb. 14.1). Die Abweichung der i-ten Einzelmessung lautet
Δi = ỹ(xi ) = [mxi + b] − yi .
(14.3)
Der Ansatz der minimalen Fehlerquadrate liefert gemäß Gl. (14.2)
Δ=
n
Δ2i
=
n
i=1
!
[mxi + b − yi ]2 =
min. .
(14.4)
i=1
Bei dem in Gl. (14.4) geforderten Minimum müssen die partiellen Ableitungen
nach den unbekannten Koeffizienten m und b gleich Null sein. Das führt zu
der im folgenden beschriebenen Ermittlung von Steigung und Achsenabschnitt
der Ausgleichsgeraden.
y(x)
y4
Δ4
y3
Δ3
Δ2
y2
y1
Δ1
x1
x2
x3
x4
x
Abb. 14.1: Ausgleichsgerade zur linearen Approximation aufgenommener Meßwerte
14.1 Regressionsverfahren
435
Ermittlung von Steigung m und Achsenabschnitt b der
Ausgleichsgeraden
Die partielle Differentiation von Gl. (14.4) nach m ergibt
2
n
[mxi + b − yi ]xi = 0 .
(14.5)
i=1
Aus der Differentiation nach b folgt
2
n
[mxi + b − yi ] = 0 .
(14.6)
i=1
Die Gleichungen (14.5) und (14.6) können wie folgt umgeformt werden
m
n
x2i + b
i=1
bzw.
m
n
xi =
i=1
n
n
y i xi
(14.7)
i=1
n
xi + nb =
i=1
yi .
(14.8)
i=1
Löst man dieses Gleichungssystem (Gl. (14.7) und (14.8)) nach den gesuchten
Werten m bzw. b auf, so erhält man die Geradensteigung m
n
m=
n
xi
i=1
yi − n
i=1
n
−n
i=1
n
=
xi y i −
i=1
n
i=1
und den Achsenabschnitt b
1
b=
n
"
x2i −
n
i=1
n
i=1
1
n
xi y i
i=1
2
xi
n
n
xi
i=1
1
n
yi − m
n
(14.9)
x2i
n
yi
i=1
2
xi
i=1
n
#
xi
.
(14.10)
i=1
Die Koeffizienten m und b lassen sich nach dem in Abb. 14.2 gezeigten Schema berechnen. Nachdem die Koeffizienten der Ausgleichsgeraden bestimmt
wurden, stellt sich im allgemeinen die Frage nach der Qualität dieser linearen
Approximation, d.h. nach der Güte bei der linearen Regression. Um letztlich die Vertrauensbereiche für die Parameter der Ausgleichsgeraden angeben
zu können, sind noch einige mathematische Definitionen notwendig, die im
folgenden Abschnitt (Kap. 14.1.2) behandelt werden.
436
14 Regression, lineare Korrelation und Hypothesen-Testverfahren
Schema zur linearen Regression:
Berechnung einer Ausgleichsgeraden aus n Meßwertepaaren {xi , yi }
1. Berechnung der Mittelwerte
μx = x =
n
1
xi
n i=1
μy = y =
n
1
yi
n i=1
2. Berechnung von 3 Hilfsgrößen1
Qx =
s2x (n
− 1) =
n
n
(xi − x) =
2
i=1
Qy =
s2y (n
− 1) =
n
i=1
(yi − y) =
2
i=1
Qxy = sxy (n − 1) =
1
−
n
x2i
n
n
yi2
i=1
1
−
n
n
2
xi
i=1
n 2
yi
i=1
(xi − x) (yi − y)
i=1
=
n
xi yi −
i=1
n
n
1 xi
yi
n i=1 i=1
3. Berechnung der Koeffizienten m und b:
Steigung2
m = Qxy /Qx
Achsenabschnitt
1
b = y − mx =
n
n
i=1
yi − m
n
xi
i=1
Abb. 14.2: Schema zur linearen Regression: Berechnung einer Ausgleichsgeraden
aus n Meßwertepaaren {xi , yi }
1
2
Qx , Qy werden auch als Summe der quadratischen Abweichungen bezeichnet (abgekürzt: S.d.q.A.). sx und sy bezeichnen die Varianz von x bzw. y und sxy die
Kovarianz zwischen x und y (siehe folgenden Abschnitt).
Die Steigung m wird auch als Regressionskoeffizient bezeichnet.
14.1 Regressionsverfahren
437
14.1.2 Güte der Anpassung bei der linearen Regression
(Varianz, Kovarianz, Restvarianz und Korrelationskoeffizient)
Nach der eigentlichen Ermittlung der Ausgleichsgeraden gilt es, die Güte dieses Ergebnisses zu beurteilen. Konkret heißt dies, Vertrauensbereiche für die
Koeffizienten m (Geradensteigung) und b (Achsenabschnitt) anzugeben. Um
diese berechnen zu können, benötigen wir quantitative Angaben für Varianz, Kovarianz, Restvarianz und Korrelationskoeffizient [50]. Diese
und weitere, im Zusammenhang dazu stehende Begriffe sollen zunächst einmal in mathematischer Form definiert werden.
Definition: Wahrscheinlichkeitsdichte
(Wahrscheinlichkeitsverteilung)
Im folgenden bezeichnet p(x) die Wahrscheinlichkeitsdichte (Wahrscheinlichkeitsverteilung) für eine Zufallsgröße x mit den Eigenschaften
+∞
p(x)dx = 1
(14.11)
−∞
p(x) ≥ 0 .
(14.12)
Die Wahrscheinlichkeit P(a), daß ein Funktionswert x kleiner oder höchstens
gleich a ist, ergibt sich aus dem Integral p(x)
a
P (a) =
p(x)dx.
(14.13)
−∞
P {a < x < b} entspricht der Wahrscheinlichkeit, mit der der Funktionswert
x zwischen den Größen a und b liegt
b
P {a < x < b} =
p(x)dx.
(14.14)
a
Definition: Gemeinsame Wahrscheinlichkeitsdichte
Die gemeinsame Wahrscheinlichkeitsdichte pxy (x, y) zweier Zufallsvariablen
pxy (x, y) ist gegeben als
∂ 2 Pxy (x, y)
∂x∂y
pxy (x, y) =
bzw.
Pxy (a, b) =
b
−∞
(14.15)
a
−∞
pxy (x, y)dxdy ,
(14.16)
wobei die Wahrscheinlichkeitsverteilung
Pxy (a, b) = P {a ≤ x ∧ b ≤ y}
(14.17)
zweier Zufallsvariablen x, y die Wahrscheinlichkeit P angibt, mit der der Funktionswert von x kleiner oder höchstens gleich a ist und der Funktionswert von
y kleiner oder höchstens gleich b ist.
438
14 Regression, lineare Korrelation und Hypothesen-Testverfahren
Definition: Erwartungswert
Der Erwartungswert eines Zufallssignales x (auch als Zufallsvariable, Zufallsgröße bzw. Zufallsprozeß bezeichnet) entspricht dem Integral über dem Produkt aus der Zufallsgröße x und seiner Wahrscheinlichkeitsdichte p(x)
+∞
E{x} =
x p(x)dx .
(14.18)
−∞
Der Erwartungswert ist ein linearer Operator.
Definition: Erwartungswert 2. Ordnung
Der Erwartungswert-Operator läßt sich auch auf das Produkt mehrerer Zufallssignale bzw. deren Potenzen anwenden [67]. Das sog. Gemeinsame Moment zweier Zufallssignale ist definiert als
+∞ +∞
μxy,kn = E{xk y n } =
xk y n pxy (x, y)dxdy .
(14.19)
−∞
−∞
Für den Spezialfall k = n = 1 folgt
+∞ μxy = E{xy} =
−∞
+∞
−∞
xypxy (x, y)dxdy .
(14.20)
Definition: Varianz
Die Varianz entspricht dem Quadrat der (empirischen) Standardabweichung
(s. auch Kap. 5.2)
Var(x) = s2x = E{(x − μx )2 } .
(14.21)
Dabei ist μx der Mittelwert der Zufallsvariablen x (siehe Abb. 14.2) und E
bezeichnet den Erwartungswert.
Die Varianz läßt sich auch mit Hilfe der Wahrscheinlichtsdichte px ausdrücken
+∞
Var(x) =
−∞
(x − μx ) px (x) dx .
(14.22)
Die Varianz s2x einer diskreten Zufallsvariablen-Stichprobe3 x1 , x2 ,
. . . , xn ist demnach folgendermaßen definiert
1 1 =
(xi − x)2 =
(xi − μx )2 .
n − 1 i=1
n − 1 i=1
n
s2x
3
n
(14.23)
Um kompatibel zu der übrigen Meßtechnik-Literatur zu bleiben, wird im folgenden nicht mehr zwischen Varianz (Gesamtheit des Loses (N → ∞)) und Schwankung (=empirische Standardabweichung (N < ∞)) unterschieden.
14.1 Regressionsverfahren
Dies läßt sich auch ausdrücken als
1 2
1
=
xi −
n − 1 i=1
n(n − 1)
n
s2x
bzw.
1 2
n
1
μx =
x −
s2x =
n − 1 i=1 i
n−1
n−1
n
" n
439
#2
xi
(14.24)
i=1
" n
#
x2i − n μx
.
(14.25)
i=1
Aus der Varianz läßt sich leicht die ebenfalls oft verwendete Summe der quadratischen Abweichung Qx (S.d.q.A.) (s. auch Abb. 14.2) errechnen
Qx = (n − 1) s2x .
(14.26)
Definition: Kovarianz
Im Zuge der Regressionsanalyse ist die Frage zu klären, inwieweit zwei Zufallsvariable x und y voneinander abhängig sind. Dies wird durch die sog.
Kovarianz festgelegt
Cov(x, y) = sxy = E{(x − μx )(y − μy )} = E{x, y} − μx μy .
(14.27)
Dabei sind μx und μy die Mittelwerte der Zufallsvariablen x und y (siehe
Abb. 14.2) und E entspricht dem Erwartungswert.
Die Kovarianz, die auch als erstes gemeinsames Moment bezeichnet
wird, läßt sich auch mit Hilfe der gemeinsamen Wahrscheinlichtsdichte pxy
ausdrücken
+∞ +∞
(x − μx )(μ − μy )pxy (x, y)dxdy .
(14.28)
Cov(x, y) =
−∞
−∞
Sie beschreibt die statistische Abhängigkeit zweier Zufallssignale. Die beiden
Zufallsvariablen sind statistisch unabhängig, wenn ihre Kovarianz Null ist
Cov(x, y) = 0. In diesem Fall berechnet sich die Wahrscheinlichkeitsdichte
p(x, y) für das gleichzeitige Eintreten der Ereignisse x und y aus dem Produkt
der Einzelwahrscheinlichkeiten p(x, y) = p(x) p(y). Außerdem gilt E{x, y} =
E{x} E{y}.
Die Kovarianz zweier diskreter Zufallsvariablenfolgen x und y ergibt sich aus
1 (xi − μx ) (yi − μy )
n − 1 i=1
n
sxy =
1
=
n−1
sxy =
" n
Qxy
.
n−1
#
xi yi − n μx μy
(14.29)
i=1
(14.30)
440
14 Regression, lineare Korrelation und Hypothesen-Testverfahren
Definition: Restvarianz
Die Restvarianz sr der Ausgleichsgeraden (Kap. 14.1.1) berechnet sich wie
folgt
"
#
Q2xy
Qy
Qy − m Qxy
2
=
1−
,
(14.31)
sr =
n−2
n−2
Qx Qy
wobei m der Steigung der Ausgleichsgeraden und n der Anzahl der behandelten Meßpunkte enspricht. Sie wird benötigt, um die Vertrauensbereiche von
Geradensteigung m und Achsenabschnitt b quantifizieren zu können.
Definition: Korrelationskoeffizient
Der Korrelationskoeffizient r ist ein die Güte der Anpassung charakterisierender Parameter (0 < r < 1). Je näher der Korrelationskoeffizient r bei 1
liegt, desto besser ist die Anpassung.
Der Korrelationskoeffizient r läßt sich aus den beiden Einzelvarianzen
sx und sy sowie der Kovarianz sxy (siehe Abb. 14.2 bzw. Gln.(14.25) und
(14.29)) bestimmen
sxy
r=
.
(14.32)
sx sy
Mit den Wurzeln der Einzelvarianzen sx und sy und der Kovarianz sxy ergibt
sich schließlich der Korrelationskoeffizient, der die Güte der Anpassung der
Ausgleichsgeraden beschreibt
n 2
n
1
2
xi − n
xi
sxy
Qxy
i=1
rxy =
=
= m i=1
(14.33)
2 .
n
n
sx sy
Qx Qy
!
1
2
yi − n
yi
i=1
i=1
Angabe der Vertrauensbereiche für die Parameter der
Ausgleichsgeraden
Mit obigen Definitionsgleichungen kann schließlich die Angabe der Vertrauensbereiche (Konfidenzintervalle) für die Parameter m und b der Ausgleichsgeraden bzw. deren Ordinatenwerte erfolgen
n
s2 2
m ± t(n − 2, P )! r
x
n Qx i=1 i
(14.34)
b ± t(n − 2, P )
s2r
Qx
(14.35)
14.1 Regressionsverfahren
y ± t(n − 2, P )
(x − x)2 n(s2x − m2 s2x ) + s2x
.
n (n − 2) s2x
441
(14.36)
Der Vertrauensfaktor t ergibt sich nach Vorgabe der gewünschten statistischen
Sicherheit P [%] aus der Student-Verteilung (s. Tab. 5.2) für die Ereignisanzahl
(n − 2). Die Anzahl der betrachteten Meßpunkte beträgt n.
Tip:
Diese Berechnungen können mit dem Programm
berechne_regressionsgerade.vi auf der CDROM
nachvollzogen werden. Es können simulierte Messwerte
eingelesen, die statistischen Daten berechnet und Regressionsgeraden ermittelt werden.
14.1.3 Ausgleichspolynome
Die Erweiterung der linearen Regression (Kap. 14.1.1) führt zur polynomialen Regression, bei der die Anpaßkure ỹ durch ein Polynom p-ten Grades
beschrieben wird
ỹ = a0 + a1 x + a2 x2 + . . . ap xp .
(14.37)
Die Vorgehensweise soll zunächst anhand des folgenden Beispiels verdeutlicht
werden. Die Anpaßkurve wird hier in Form eines Polynoms dritten Grades
beschrieben
ỹ(x) = a0 + a1 x + a2 x2 + a3 x3 .
(14.38)
Das bereits oben angewandte Gaußsche Prinzip der kleinsten Quadrate (Gaußsches Minimalprinzip) soll auch hier Anwendung finden
Δ=
n
Δ2i =
i=1
n
!
[ỹ(xi ) − yi ]2 =
min. .
(14.39)
i=1
Dabei werden wiederum n Meßwertepaare {xi , yi } vorausgesetzt. Das Nullsetzen der partiellen Ableitungen nach den Koeffizienten ai (i = 1, 2, 3)
∂Δ
∂Δ
∂Δ
∂Δ
=
=
=
=0
∂a0
∂a1
∂a2
∂a3
führt zu folgendem Gleichungssystem
⎛
⎞
n
n
n
n
xi
x2i
x3i
⎜
⎟
i=1
i=1
i=1
⎜ n
⎟
n
n
n
⎜
⎟
2
3
4
⎜
⎟
x
x
x
x
⎜ i=1 i i=1 i i=1 i i=1 i ⎟
⎜
⎟
n
n
n
n
⎜
⎟
2
3
4
5⎟
⎜
xi
xi
xi
xi ⎟
⎜
⎜ i=1 i=1 i=1 i=1 ⎟
⎝
⎠
n
n
n
n
x3i
x4i
x5i
x6i
i=1
i=1
i=1
i=1
(14.40)
⎛ ⎞
n
yi
⎜ i=1
⎟
a0
⎜ n
⎟
⎜ ⎟ ⎜
⎟
⎜a ⎟ ⎜
⎟
x
y
⎜ 1 ⎟ ⎜ i=1 i i ⎟
⎜ ⎟=⎜
⎟.
n
⎜ ⎟ ⎜
⎟
2 ⎟
⎜ a2 ⎟ ⎜
xi y i ⎟
⎝ ⎠ ⎜
⎜ i=1
⎟
⎝
⎠
n
a3
3
xi y i
⎛
⎞
i=1
(14.41)
442
14 Regression, lineare Korrelation und Hypothesen-Testverfahren
Die Lösung dieses Gleichungssystems ergibt schließlich die gesuchten Koeffizienten ai (i = 0, 1, 2, 3) des Polynoms.
14.1.4 Mehrfache lineare Regression
Die mehrfache lineare Regression (auch als multiple lineare Regression bezeichnet) ist eine Erweiterung der einfachen linearen Regression. Dabei hängt
ein Meßergebnis y linear von nunmehr mehreren Variablen x1 , x2 , . . . xp (man
spricht in diesem Zusammenhang auch von Covariablen) ab
y = a 0 + a 1 x1 + a 2 x2 + . . . + a p xp + E ,
(14.42)
wobei E eine Störgröße repräsentiert, also eine stochastische Variable (Zufallsvariable). Damit ist das Ergebnis ebenfalls eine Zufallsvariable. Die Aufgabe
der mehrfachen linearen Regression ist es nun, die abhängige Variable y als
Funktion mehrerer (in Bezug auf die Laufvariable i) unabhängiger Variablen,
die in Form eines Variablenvektors [xip ] = (xi1 , xi2 , . . . , xip ) zusammengefaßt
werden, mit Hilfe eines Schätzwertes ŷ vorherzusagen
ŷ = b0 + b1 x1 + b2 x2 + . . . + bp xp .
(14.43)
Dabei bilden die bj (j = 1, 2, . . . , p) die Elemente des Vektors der geschätzten
Regressionskoeffizienten.
Wir wollen davon ausgehen, daß für jeden Vektor [xip ](i = 1, 2, . . . , n)
jeweils n Meßwerte yi (i = 1, 2, . . . , n) vorliegen. Somit ergibt sich für jede
Beobachtung (Messung) i(i = 1, 2, . . . , n) eine Gleichung der Form
yi = a0 + a1 xi1 + a2 xi2 + . . . + ap xip + Ei .
(14.44)
Das daraus resultierende Gleichungssystem läßt sich mit Hilfe der folgenden
[n × (p + 1)]-Matrix [X]
⎛
1 x11 x12 . . . x1j . . . x1p
⎜
⎜1 x x ...
21 22
⎜
⎜
⎜
⎜ ..
⎜.
⎜
[X] = ⎜
⎜1 x x ...
i1
i2
⎜
⎜
⎜.
⎜.
⎜.
⎝
⎞
⎟
x2j . . . x2p ⎟
⎟
⎟
⎟
.. ⎟
..
. ⎟
.
⎟
⎟
xij . . . xip ⎟
⎟
⎟
.. ⎟
..
⎟
. ⎟
.
⎠
1 xn1 xn2 . . . xnj . . . xnp
(14.45)
14.1 Regressionsverfahren
sowie der n-dimensionalen Vektoren
⎛ ⎞
y1
⎜ ⎟
⎜ ⎟
⎜ y2 ⎟
⎜ ⎟
⎜ ⎟
⎜ ⎟
[y] = ⎜ ... ⎟ ,
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎜ yi ⎟
⎝ ⎠
yn
und dem [p + 1]-dimensionalen Vektor
⎛
⎛
E1
⎞
⎜
⎟
⎜
⎟
⎜ E2 ⎟
⎜
⎟
⎜
⎟
⎜ .. ⎟
E=⎜ . ⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜ Ei ⎟
⎝
⎠
En
a0
443
(14.46)
⎞
⎜ ⎟
⎜a ⎟
⎜ 1⎟
⎜ ⎟
⎜ ⎟
⎜ a2 ⎟
⎜ ⎟
⎟
[a] = ⎜
⎜ . ⎟
⎜ .. ⎟
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎜ aj ⎟
⎝ ⎠
ap
(14.47)
wie folgt darstellen
[y] = [X] [a] + [E] .
(14.48)
Die einfache lineare Regression ergibt sich aus obigen Gleichungen für p = 1.
Der Fall p ≥ 2 repräsentiert die mehrfache lineare Regression. Wie bei der
linearen Regression wird wiederum die Summe der quadratischen Abweichungen minimiert.
Nach dem sog. Gauß-Markov-Theorem erhält man schließlich den Vektor
der geschätzten Regressionskoeffizienten [b] als [96]4
⎛ ⎞
b0
⎜ ⎟
⎜b ⎟
⎜ 1⎟
⎜ ⎟
⎜ ⎟
⎜ .. ⎟
⎜ . ⎟ −1
⎜ ⎟
[b] = ⎜ ⎟ = [X]T [X]
[X]T [y] .
(14.49)
⎜b ⎟
⎜ j⎟
⎜ ⎟
⎜ . ⎟
⎜ . ⎟
⎜ . ⎟
⎝ ⎠
bp
4
Um die hier verwendete Schreibweise mit der Darstellung in [96] vergleichbar zu
machen, ist für die Matrix [X] deren Transponierte [X]T zu verwenden (siehe S.
62 in [96]).
444
14 Regression, lineare Korrelation und Hypothesen-Testverfahren
Dabei bezeichnet [X]T die Transponierte der Matrix [X]. Dieser Schätzer
ist der sog. beste lineare unverzerrte Schätzer (Best Linear Unbiased
Estimator = BLUE). Mit Hilfe dieses Schätzers (Minimum-Quadrat-Schätzer)
ergibt sich folgendes Gleichungssystem
[y] = [X] [b] + [e] = [ŷ] + [e] ,
(14.50)
wobei [ŷ] die Schätzwerte von [y] enthält und [e] den Vektor der Residuen
repräsentiert. Der Vektor der Schätzwerte berechnet sich also aus
[ŷ] = [X] [b] = [X]([X]T [X])−1 [X]T [y] = [H][y] ,
(14.51)
wobei die [n×n]-Matrix [H] als sog. Hat-Matrix (Hut-Matrix) bezeichnet wird.
Die Residuen ergeben sich demnach wie folgt
[e] = [y] − [ŷ] = [y] − [H] [y] .
(14.52)
Im allgemeinen interessiert man sich für die sog. Prognose ŷ0 von [y] für ein
gegebenes Wertetupel [x0 ] (= Meßstelle [x01 , x02 , . . . , x0p ]). Sie berechnet sich
zu
ŷ0 = b0 + b1 x01 + b2 x02 + . . . + bp x0p = [x0 ]T [b] .
(14.53)
14.2 Lineare Korrelation
Die lineare Korrelation beschäftigt sich mit der Frage, inwieweit Wertepaare
{xi , yi } linear abhängig sind. Im Gegensatz zur linearen Regression wird hier
y nicht als abhängige und x nicht als unabhängige Variable bezeichnet.
Da nunmehr keine Unterscheidung nach abhängiger und unabhängiger Variable erfolgt, ist die Definition von zwei Ausgleichsgeraden sinnvoll, nachdem
die Wertepaare {xi , yi } in ein x-y-Diagramm eingetragen wurden. Zur Festlegung der Geraden wird wiederum das bereits bei der linearen Regression eingesetzte Verfahren der Fehlerquadratminimierung (Gaußsches Minimalprinzip)
eingesetzt (s. Kap. 14.1.1).
Die beiden Ausgleichsgeraden (Abb. 14.3) lassen sich wie folgt definieren
ỹ = m1 x + b1
(14.54)
x̃ = m2 y + b2 .
(14.55)
bzw.
Daraus resultieren zwei Möglichkeiten, die Fehlerquadratminimierung durchzuführen
!
(ỹ − yi )2 =
min.
(14.56)
bzw.
!
(x̃ − xi )2 =
min. .
(14.57)
14.2 Lineare Korrelation
445
y
x
Abb. 14.3: Meßwertepaare {xi , yi }, die durch zwei Ausgleichsgeraden gemäß
Gl. (14.54) bzw. Gl. (14.55) approximiert werden.
Im allgemeinen führt dieser Prozeß zu unterschiedlichen Geraden.
Für den Fall, daß vollkommene lineare Unabhängigkeit zwischen den Werten der Variablen x und y besteht, streben die beiden Steigungen m1 und m2
gegen Null (Abb. 14.4). Für den Fall, daß die beiden Geraden zusammenfallen
(Abb. 14.5), besteht ein direkter funktionaler Zusammenhang.
Je nach Grad der linearen Abhängigkeit variieren die Geradensteigungen
also zwischen den Werten m1 = m2 = 0 (lineare Unabhängigkeit) und einem
oberen Wert m1 = 1/m2 (vollständige lineare Abhängigkeit). Da dieser obere
y
m 2= 0
m 1= 0
x
Abb. 14.4: Fall der vollständigen linearen Unabhängigkeit (m1 = m2 = 0)
446
14 Regression, lineare Korrelation und Hypothesen-Testverfahren
y
1
m 1= m
2
x
Abb. 14.5: Fall des funktionalen Zusammenhangs: Die beiden Ausgleichsgeraden
fallen zusammen.
Wert aber nicht von vorneherein feststeht, läßt sich der Grad der linearen
Abhängigkeit erst nach einer Normierung beurteilen. Dies führt zu einer normierten Steigung r, die dem Korrelationskoeffzient entspricht (siehe auch
Gl. (14.32) und Gl. (14.33)).
Im Gegensatz zur Kovarianz ist der Korrelationskoeffizient eine reine Maßzahl ohne Einheit. Der Korrelationskoeffizient nimmt Werte zwischen −1 und
+1 an (−1 ≤ r ≤ +1).
Ein Korrelationskoeffizient r = 0 bedeutet, daß keine lineare Abhängigkeit
besteht. Bei vollkommener linearer Abhängigkeit nimmt r den Wert +1 bzw.
−1 an. Das Vorzeichen beschreibt dabei die Steigungsrichtung der gemeinsamen Geraden (Abb. 14.5).
Der Korrelationskoeffizient läßt sich wie folgt angeben
n
Qxy
r=
= %
Qx Qy
n
! y2 −
i=1
i
xi y i −
i=1
1
n
n
i=1
1
n
n
i=1
2 ' %
yi
xi
n
i=1
n
yi
i=1
x2i −
1
n
n
2 '
. (14.58)
xi
i=1
Bei der Beurteilung der linearen Abhängigkeit anhand des Korrelationskoeffizienten muß die Stichprobenanzahl mit ins Kalkül gezogen werden. So liefern
beispielsweise zwei Wertepaare immer den Wert r = 1. Aus diesem Grund
ist zu dieser Beurteilung noch der im folgenden behandelte Vertrauensbereich
von r hinzuziehen.
14.3 Testverfahren (Hypothesen-Testverfahren)
447
Vetrauensbereich des Korrelationskoeffizienten
Da der nach Gl. (14.58) ermittelte Korrelationskoeffizient nur ein Schätzwert
des Korrelationskoeffizienten ρ der Grundgesamtheit (setzt unendlich viele
Messungen voraus) darstellt, sollte man den Vertrauensbereich für r ermitteln, um eine Aussage der möglichen Abweichungen von ρ als Funktion einer
gewählten statistischen Sicherheit zu erhalten.
Um den Vertrauensbereich eines anhand einer Stichprobe mit n Einzelmessungen ermittelten Korrelationskoeffizienten anzugeben, bedient man sich
des nachfolgenden Schemas in Abb. 14.6. Die Grundlagen hierzu findet der
interessierte Leser beispielsweise in [69].
Korrelation und Kausalität
Ein hoher Korrelationskoeffizient ist auf eine starke lineare Abhängigkeit
zurückzuführen. Daraus darf aber nicht unmittelbar auf eine Kausalität
im Sinne eines Ursache-Wirkungs-Prinzips geschlossen werden. Es gibt
unzählige Beispiele für Scheinkorrelationen oder sogar Unsinnrelationen, die
durchaus nicht auf eine gemeinsame Ursache zurückzuführen sind. Ein kausaler Zusammenhang muß zunächst einmal von der Sache her begründet sein.
Anhand einer dazu durchgeführten Korrelation läßt sich lediglich prüfen, ob
eine Hypothese zu einem bestimmten Ursache-Wirkungs-Prinzip hält oder
nicht. Es darf aber keinesfalls aus einem hohen Korrelationsgrad unmittelbar auf einen entsprechenden Ursache-Wirkungs-Zusammenhang geschlossen
werden.
Als Beispiel könnte angeführt werden, daß die steigende Lebenserwartung
und die steigende Preisentwicklung sicherlich keinen unmittelbaren kausalen
Zusammenhang aufweisen, aber dennoch zwischen beiden ein von Null verschiedener Korrelationskoeffizient besteht.
14.3 Testverfahren (Hypothesen-Testverfahren)
14.3.1 Testen von Hypothesen, Entscheidungen
Die Wahrscheinlichkeitsverteilung, welche die Grundgesamtheit beschreibt,
wird als wahre Wahrscheinlichkeitsverteilung bezeichnet. Diese wahren
Verteilungen sind aber in der praktischen Meßtechnik nicht bekannt. Mit Hilfe von sog. Tests muß daher des öfteren entschieden werden, ob bestimmte
Vermutungen über die Wahrscheinlichkeitsverteilungen bzw. deren Parameter
zutreffen oder nicht.
Zur Durchführung eines Tests stellt man eine Arbeitshypothese auf. Diese
wird als Nullhypothese H0 bezeichnet. Die dieser Nullhypothese widersprechende Vermutung wird Alternativhypothese H1 genannt.