Blatt 03 - Universität Würzburg

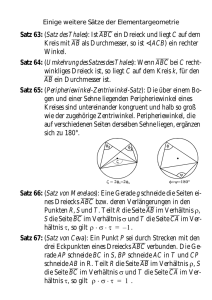
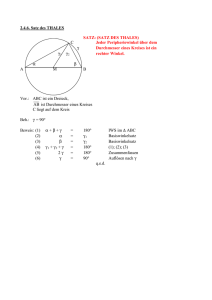
Prof. Dr. Fabian Wirth, Dr. Michael Schönlein
Institut für Mathematik, Universität Würzburg
30. Oktober 2012
Analytische Geometrie — 3. Übung
Aufgabe 1. (5 Punkte) Verallgemeinerung des Satzes von Thales
Gegeben sei ein Kreis und die Punkte A, B auf dem Kreis. Der Winkel ϕb bei
einem Punkt C heißt Peripheriewinkel zum Bogen b (vgl. Skizze). Der Winkel
µb heißt Zentriwinkel zum Bogen b (vgl. Skizze). Zeigen Sie, dass alle Peripheriewinkel über einem Kreisbogen gleich groß sind und dem halben Zentriwinkel
entsprechen.
Aufgabe 2. (2 Punkte)
Gegeben sei ein Kreis und zwei Sehnen AA0 und BB 0 welche sich im Punkt
P schneiden. Zeigen Sie, dass das Produkt der Sehnenabschnitte konstant ist,
d.h. es gilt
AP · A0 P = BP · B 0 P .
Hinweis: Verwenden Sie Aufgabe 1.
Aufgabe 3. (3 Punkte)
Das Dreieck ∆ABC sei gleichseitig. Die Punkte P und Q teilen jeweils eine
Seite von ∆ABC. Die Verlängerung der Strecke P Q schneide den Umkreis
von ∆ABC im Punkt K. Zeigen Sie, dass der Punkt Q die Strecke P K im
Verhältnis des goldenen Schnitts teilt.
Hinweis: Verwenden Sie Aufgabe 2.
Abgabe ist am Mittwoch, den 7. 11. 2012 in der Vorlesung.