Wechselstromkreis mit verschiedenen Bauteilen
Werbung

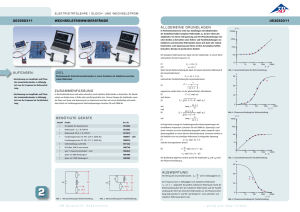
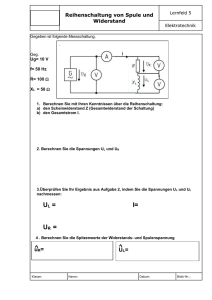
Protokoll vom 08.05.07 und 11.05.07 von Christian Suhr und Thomas Vogelsang Wechselstromkreis mit verschiedenen Bauteilen Im Folgenden werden nun die Auswirkungen eines ohmschen Widerstands, eines induktiven Widerstands (Spule) und eines kapazitiven Widerstands (Kondensator) auf den Strom und die Spannung in einer Reihen- bzw. Parallelschaltung untersucht und beschrieben. (1) Reihenschaltung Versuchsaufbau: Betrachtet wird diese Schaltung: Da es sich hier um eine Reihenschaltung handelt, fließt in der gesamten Schaltung der gleiche Strom i. Die Spannung u wird jedoch auf die einzelnen Bauteile, also auf den Widerstand R, die Spule L und den Kondensator C aufgeteilt. Die Gesamtspannung uges bzw. uLCR hat eine bestimmte Phasendifferenz φ zum Strom i. - Seite 1 von 7 - Protokoll vom 08.05.07 und 11.05.07 von Christian Suhr und Thomas Vogelsang Zum Versuch: Der Generator erzeugt eine Wechselspannung uG mit einer bestimmten Frequenz ω. Gemessen wird der Strom i und außerdem die Teilspannungen an den einzelnen Bauteilen. Diese können aber auch mit folgenden Formeln berechnet werden: Für den ohmschen Widerstand gilt die Formel: ûR = R î Für den induktiven Widerstand gilt die Formel: ûL = XL î ; mit XL = ω L Für den kapazitiven Widerstand gilt die Formel: ûC = XC î ; mit XC = Um nun den Zusammenhang besser zu verstehen, wird folgendes Phasendiagramm betrachtet: Wie zu sehen ist, dreht sich das Diagramm gegen den Uhrzeigersinn. Bei der Reihenschaltung fließt – wie bereits erwähnt – überall der gleiche Strom i. î beschreibt dabei den Scheitelwert, also Maximalwert, des Stroms. Beim ohmschen Widerstand sind der Strom und die Spannung uR in Phase. → Keine Phasenverschiebung ; gleiche Richtung wie der Strom I Beim Kondensator muss erst ein Strom fließen, bevor es eine Spannung uC geben kann. - Seite 2 von 7 - Protokoll vom 08.05.07 und 11.05.07 von Christian Suhr und Thomas Vogelsang → Eine Phasenverschiebung um Umgekehrt ist es bei der Spule. Aufgrund der Induktion durch die vom Wechselstrom hervorgerufene Magnetfeldänderung entsteht eine Induktionsspannung, die nach Lenz der Ursache der Induktion durch eine Verzögerung der Stromänderung entgegenwirkt. → Eine Phasenverschiebung um . Jetzt kann mithilfe des Satzes des Pythagoras und den Teilspannungen ûL, ûC und ûR die Gesamtspannung ûLCR ausgerechnet werden: Um nun den Gesamtwiderstand dieser Reihenschaltung zu ermitteln, benötigt man die Formel für die Impedanz Z: (jeweils die Scheitelwerte) In diesem Fall ist die gesamte Spannung und der gesamte Strom ist î. Also: Zieht man die Wurzel aus dem gesamten Bruch, so steht im Nenner unter der Wurzel das Quadrat der Stromstärke. Da die einzelnen Summanden denselben Nenner haben, kann die Formel auch umgeschrieben und dann die einzelnen Formeln der Teilwiderstände R, XL und XC (Formel s.o.) eingesetzt werden: - Seite 3 von 7 - Protokoll vom 08.05.07 und 11.05.07 von Christian Suhr und Thomas Vogelsang Die Phasendifferenz φ lässt sich ebenfalls berechnen. Dazu betrachtet man erneut das Phasendiagramm und stellt fest, dass sich φ wie folgt berechnen lässt: (Da wir die Phasenverschiebung immer positiv betrachten, werden dem Zähler Betragstriche hinzugefügt): (2) Parallelschaltung Versuchsaufbau: Betrachtet wird diese Schaltung: Hierbei handelt es sich um eine Parallelschaltung. Das bedeutet, dass die gleiche Spannung u in der gesamten Schaltung vorhanden ist, sich der Strom i jedoch auf die einzelnen Bauteile, also auf den Widerstand R, die Spule L und den Kondensator C aufteilt. Also gilt: -uG = uR = uL = uC. - Seite 4 von 7 - Protokoll vom 08.05.07 und 11.05.07 von Christian Suhr und Thomas Vogelsang Auch hier hat der Gesamtstrom iges bzw. iLCR eine bestimmte Phasendifferenz φ zur Spannung u. - Seite 5 von 7 - Protokoll vom 08.05.07 und 11.05.07 von Christian Suhr und Thomas Vogelsang Zum Versuch: Der Generator erzeugt wieder eine Wechselspannung uG mit einer bestimmten Frequenz ω. Erneut wird die Spannung u und außerdem die Teilströme an den einzelnen Bauteilen gemessen. Es gelten die gleichen Formeln wie in (1) Reihenschaltung, deshalb erfolgt die Beschreibung des Phasendiagramms als kleine Übersicht Übersicht - Das Diagramm dreht sich gegen den Uhrzeigersinn - Betrachtet werden die Scheitelwerte des Stroms bzw. Spannung - Ohmscher Widerstand: Spannung und Strom sind in Phase - Induktiver Widerstand: Zuerst Spannung, dann Strom → - Kapazitiver Widerstand: Zuerst Strom, dann Spannung → Jetzt kann mithilfe des Satzes des Pythagoras und den Teilströmen îL, îC und îR die Gesamtspannung îLCR ausgerechnet werden: Wieder gilt: (jeweils die Scheitelwerte) - Seite 6 von 7 - Protokoll vom 08.05.07 und 11.05.07 von Christian Suhr und Thomas Vogelsang In diesem Fall ist die gesamte Spannung und der gesamte Strom ist û. Also: Diesmal sind die Summanden im Nenner, also muss man zuerst den Kehrwert nehmen, um weiter rechnen zu können. Dann kann die Formel auch wieder umgeschrieben und die einzelnen Formeln der Teilwiderstände R, XL und XC (Formel s.o.) eingesetzt werden: Auch die Phasendifferenz φ lässt sich wieder berechnen. Dazu betrachtet man erneut das Phasendiagramm und stellt fest, dass sich φ wie folgt berechnen lässt: (Da wir die Phasenverschiebung immer positiv betrachten, werden dem Zähler Betragstriche hinzugefügt): - Seite 7 von 7 -