Elektrischer Schwingkreis (LCR)

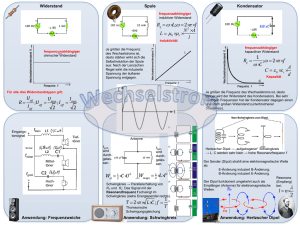
Physikpraktikum Anleitung
Elektrischer Schwingkreis (LCR)
Elektrische Schwingkreise spielen in vielen technischen Anwendungen (z.B. Taktgeber, Radioempfänger) eine
entscheidende Rolle.
Ziel
Ein Kondensator, eine Spule und ein ohmscher Widerstand werden seriell mit einem Frequenzgenerator verbunden.
• Sie üben an einem elektrischen Schwingkreis den Umgang mit dem Kathodenstrahloszilloskop.
• Sie können eine Resonanzkurve qualitativ beschreiben und ausmessen.
Experiment
Material
Frequenzgenerator (FG) und Kathodenstrahloszilloskop (KO), Spule, Kondensatoren und Widerstände, Multimeter (zur Messung von Widerstand, Kapazität, und als Frequenzmesser). Dazu 1 Multimeter (Amprobe) für
alle um die Induktivität zu messen.
Durchführung
a) Wählen Sie einen Kondensator mit Kapazität C, eine Spule mit Induktivität L und einen Widerstand R.
Die Resonanzfrequenz soll bei 1-10kHz liegen und die Dämpfung durch den Widerstand nicht zu stark
sein.
b) Bauen Sie die nebenstehende Schaltung auf. CA und CB sind Kanal 1 und Kanal 2 des Oszilloskops.
Die Masseanschlüsse des Oszilloskops müssen auf gleichem Potential liegen. Der Frequenzgenerator soll
sinusförmige Wechselspannung erzeugen. Lassen Sie die Schaltung kontrollieren, bevor Sie den Generator
einschalten.
c) Kontrollieren Sie, dass eine Resonanz sichtbar ist, bevor Sie mit den Messungen beginnen. Notieren Sie
die Nennwerte der elektrischen Elemente und kontrollieren Sie diese durch eine separate Messung.
d) Messen Sie dann die Generatorspannung (Kanal 1), die Spannung über dem Widerstand (Kanal 2) und
die zeitliche Versetzung der zwei Spannungssignale als Funktion der Frequenz.
Ziel ist eine schöne graphische Darstellung des Spannungsverhältnisses und der Phasenverschiebung als
Funktion der Frequenz. Sie sollten also sicher bis zur doppelten Resonanzfrequenz Messwerte haben und
mindestens 15 Punkte messen. Der Oszilloskop kann sowohl die Frequenz als auch die Spannungen (peak
to peak Uss ) messen.
AK
1
Physikpraktikum Anleitung
e) Stellen Sie die Generatorspannnung und die Spannung über den Widerstand (von Messung d) als XY
-Diagramm (Lissajous-Figur) auf dem Oszilloskop dar (→ Display → Format → XY). Dabei werden die
zwei Spannungen gegeneinander aufgetragen, wobei auf der X-Achse die Generatorspannung während
auf der Y -Achse die Spannung über dem Widerstand abzulesen sind. Erhöhen Sie die Frequenz und
beobachten Sie wie sich die Figur ändert. Skizzieren Sie einige davon und notieren Sie die dazugehörigen
Spannungswerte.
Auswertungen
1) Stellen Sie das Spannungsverhältnis (Spannung über Widerstand zu Generatorspannung) als Funktion der
Frequenz und Phasenverschiebung1 als Funktion der Frequenz graphisch dar. Zeichnen Sie die theoretisch
zu erwartende Funktionen dazu (Stichwort: Impedanz). Versuchen Sie auch, die Parameter dieser Funktion
durch eine Kurvenanpassung zu bestimmen. Interpretieren Sie die Messungen. Beachten Sie, dass der
Gesamtwiderstand im Kreis grösser als der Widerstandswert des Widerstandselements ist. Diskutieren Sie
allfällige Unterschiede und Genauigkeiten.
2) Interpretieren Sie die Lissajous-Figuren (z.B. die Phasenverschiebung).
Bedingungen
Falls Sie einen Bericht schreiben, geben Sie diesen mit der vollständigen Auswertung (Fehlerrechnung wo
möglich) ab. Für eine Auswertung ohne Bericht bearbeiten Sie mindestens die Aufgaben 1) ohne Fehlerrechnung.
Abgabetermin ist:
Literatur
• Theorieblätter vom Physikunterricht
• Duden Physik Abitur, Abschnitt 4.6 “Der Wechselstromkreis”
• Duden Physik Abitur, Abschnitt 4.7.2 “Elektromagnetische Schwingungen”
• http://de.wikipedia.org/wiki/Schwingkreis
• http://www.leifiphysik.de/elektrizitaetslehre/wechselstromtechnik
1 Aus
AK
der Zeitverschiebung können Sie die Phasenverschiebung berechnen ( ∆ϕ
=
2π
∆T
T
mit T = 1/f ).
2