Lernbereich 8: Deterministisches Chaos Experimente, Simulationen
Werbung

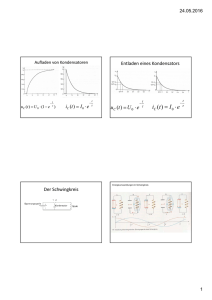
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote • • • • • • • Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen … EXPERIMENTIERPHASE 1 Modellierung und Moebius Populationsdynamik Theoretische Hintergründe für Beispiele aus Mechanik und Elektrik • EXPERIMENTIERPHASE 2 • Wege ins Chaos • Herzrhythmus und Physik 1. Lineare und nichtlineare Systeme Linearer Federschwinger Ebenes Federpendel •• m ⋅ x+ k ⋅ x = 0 •• x ⋅ FFeder ( x, y ) = 0 l ( x, y ) •• y m ⋅ y+ ⋅ FFeder ( x, y ) = 0 l ( x, y ) m ⋅ x+ Drehpendel Drehpendel mit Unwucht Elektrischer Schwingkreis Elektrischer Schwingkreis mit nichtlinearem Blindelement Fadenpendel mit geringer Auslenkung Fadenpendel mit beliebiger Auslenkung (Stabpendel) 2 •• m ⋅ l ⋅ ϕ + m ⋅ g ⋅ l ⋅ sin ϕ = 0 •• m ⋅ l ⋅ϕ + m ⋅ g ⋅ l ⋅ϕ = 0 2 Parabelförmige Kugelmulde Kugelschale mit Mulden Magnetpendel, Doppelpendel, … 2. Nichtlineare Systeme Dissipative Systeme (Energiedurchströmung) Konservative Systeme (Energieerhaltung) Lorenzmodell Einfach- und Doppelpendel Getriebenes Drehpendel mit Unwucht und Wirbelstromdämpfung Magnetpendel (ohne Dämpfung) Getriebener nichtlinearer elektrischer Schwingkreis mit ohmschem Widerstand Getriebenes Einfachpendel mit Reibung Begriffe: Bifurkation Intermittenz Seltsamer Attraktor Planetensystem (Dreikörperproblem) 3. Nichtlineare Rückkopplung 3.1. Logistische Abbildung xn +1 = r ⋅ xn ⋅ (1 − xn ) = r ⋅ xn − r ⋅ xn2 3.2. Pohlsches Drehpendel 3.3. Elektrischer Schwingkreis 3.1. Logistische Abbildung Populationsmodell Na Nn= c*Na aktuelle Tierzahl nächste Generation c : Reproduktionsfaktor c > 1 => Überbevölkerung c < 1 => Aussterben Dämpfungsfaktor (Nmax – Na)/Nmax=(1- Na/Nmax) Nmax – maximal „ernährbare“ Tierzahl mit Na/Nmax = xa Nn/Nmax = xn c = r*(1-xa) 0<xa<1 0<xn<1 folgt die Gleichung für die logistische Abbildung xn = r*xa*(1-xa) oder xn+1 = r*xn*(1-xn) Iteration und Nichtlinearität nichtlineare Rückkopplung x n + 1 = r ⋅ x n ⋅ (1 − x n ) = r ⋅ x n − r ⋅ x n2 0 < r ≤ 3,0 „gewöhnliches Verhalten“ 3,0 < r ≤ 4,0 „überraschendes Verhalten“ Iteration und Feigenbaum-Diagramm Iteration x x r = 2,8 x r = 3,2 r = 4,0 x r Feigenbaum-Diagramm 3.2. Pohlsches Drehpendel Nichtlinearität Drehschwinger mit Zusatzmasse Feder Antrieb Energiezufuhr Wirbelstromdämpfung Energieabgabe Energie strömt durch ein nichtlineares System (nichtlineares dissipatives System) 3.2.1. Drehpendel ohne Zusatzmasse j 0 90 120 0 12 90 harmonische Reaktion 15 0 Exzenter harmonische Anregung 60 lineare Spiralfeder 30 60 30 150 Wirbelstrombremse Energiezufuhr •• Energieabgabe • J 0 ⋅ϕ = − D ⋅ϕ − δ ⋅ϕ + M 0 ⋅ sin ω 0 t Energiezufuhr Linearität durch Exzenter durch Spiralfeder Energieabgabe durch Wirbelstrombremse Diagramme des linearen Drehpendels j Phasendiagramm harmonische Anregung j j j harmonische Reaktion t Zeitdiagramm 3.2.2. Drehpendel mit Zusatzmasse j 0 0 12 120 Exzenter 90 90 60 lineare Spiralfeder harmonische Anregung 30 60 30 Nichtlinearität durch Zusatzmasse (m) nichtharmonische Reaktion 15 0 150 Wirbelstrombremse Energiezufuhr Energieabgabe •• • J Z ⋅ ϕ = − D ⋅ ϕ + m ⋅ g ⋅ r ⋅ sin ϕ − δ ⋅ ϕ + M 0 ⋅ sin ω 0 t Nichtlinearität durch Zusatzmasse Energiezufuhr durch Exzenter Energieabgabe durch Wirbelstrombremse Diagramme des nichtlinearen Drehpendels Phasendiagramm j harmonische Anregung j j j nichtharmonische Reaktion Zweite Bifurkation t Zeitdiagramm 3.3. Elektrischer Schwingkreis Energiezufuhr Generator Energieabgabe Nichtlinearität Diode als nichtlineare Kapazität Ohmscher Widerstand mit Joulescher Abwärme Energie strömt durch ein nichtlineares System (nichtlineares dissipatives System) 3.3.1. Linearer elektrischer Schwingkreis Energiezufuhr Energieabgabe lineare Kapazität G harmonische Anregung R 30kHz L C UC harmonische Reaktion UA u L + u R + uC = u A •• ∧ 1 L ⋅ Q + R ⋅ Q + ⋅ Q = U ⋅ sin(ω ⋅ t ) C Energieabgabe durch Joulesche Wärme • Energiezufuhr durch Generator Linearität durch konstante Kapazität (und konstante Induktivität) Diagramme des linearen elektrischen Schwingkreises Phasendiagramm UC harmonische Anregung UA UC UA harmonische Reaktion t Zeitdiagramm 3.3.2. Nichtlinearer elektrischer Schwingkreis Energiezufuhr Energieabgabe nichlineare Kapazität G harmonische Anregung R 30kHz L CD(U) UD UA nichtharmonische Reaktion uL + uR + uD = u A •• • ∧ Q L ⋅ Q + R ⋅ Q + U 0 ⋅ (exp( ) − 1) = U ⋅ sin(ω ⋅ t ) Co ⋅ U o Energiezufuhr durch Generator Energieabgabe durch Joulesche Wärme Nichtlinearität durch spannungsabhängige Kapazität Diagramme des nichtlinearen elektrischen Schwingkreises Phasendiagramm UD harmonische Anregung UA UD UA nichtharmonische Reaktion t Zeitdiagramm 4. Wettervorhersage und Sensitivität J/°C t/d Min. Temperatur Median Max. Temperatur 90% Band