Inertialsysteme Zwei Inertialsysteme Nicht
Werbung
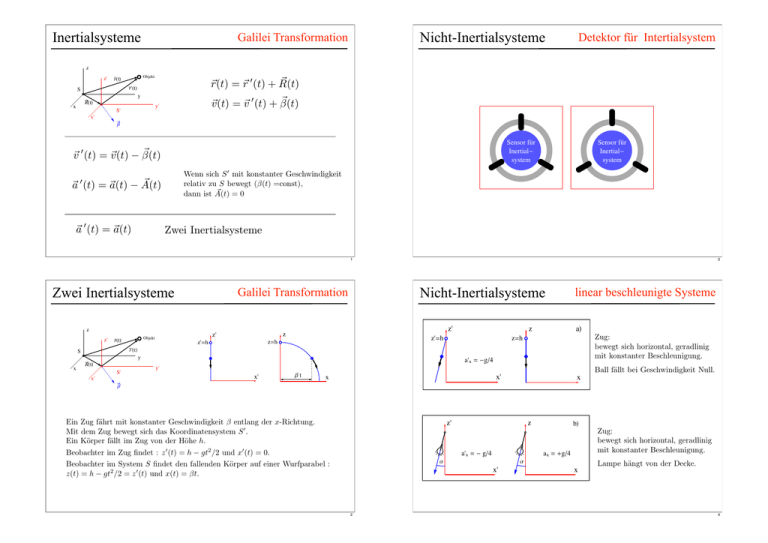
Inertialsysteme z z' ”rHtL S ”r'HtL Objekt ~v (t) = ~v 0 (t) + ~ (t) y' S' Detektor für Intertialsystem ~ ~r(t) = ~r 0 (t) + R(t) y RHtL x Nicht-Inertialsysteme Galilei Transformation x' b 0 ~ (t) 0 ~ A(t) ~v (t) = ~v (t) ~a (t) = ~a(t) ~a 0 (t) = ~a(t) Sensor für Inertialsystem Sensor für Inertialsystem Wenn sich S 0 mit konstanter Geschwindigkeit relativ zu S bewegt ( (t) =const), ~ =0 dann ist A(t) Zwei Inertialsysteme 1 Zwei Inertialsysteme z z' ”rHtL S ”r'HtL Nicht-Inertialsysteme Galilei Transformation y x RHtL S' x' linear beschleunigte Systeme aL Zug: bewegt sich horizontal, geradlinig mit konstanter Beschleunigung. z=h z'=h z=h z'=h z z' z z' Objekt 3 a'x = -gê4 y' x' bt x' x x Ball fällt bei Geschwindigkeit Null. b Ein Zug fährt mit konstanter Geschwindigkeit entlang der x-Richtung. Mit dem Zug bewegt sich das Koordinatensystem S 0 . Ein Körper fällt im Zug von der Höhe h. Beobachter im Zug findet : z 0 (t) = h gt2 /2 und x0 (t) = 0. Beobachter im System S findet den fallenden Körper auf einer Wurfparabel : z(t) = h gt2 /2 = z 0 (t) und x(t) = t. z' € € a z a'x = - gê4 a x' 2 bL Zug: bewegt sich horizontal, geradlinig mit konstanter Beschleunigung. ax = +gê4 x Lampe hängt von der Decke. 4 Nicht-Inertialsysteme Foucaultsches Pendel Nicht-Inertialsysteme Coriolis- / Zentrifugalbeschleunigung ~a 0 = ~a + 2(~v 0 ⇥ ! ~) + ! ~ ⇥ (~r 0 ⇥ ! ~) N Ω ~v 0 Drehung der Pendelebene bei Beobachtung im rotierenden Erdsystem. ~v 0 In Freiburg : 12o pro Stunde. Die Erde dreht sich unter dem Pendel, wie auch beim Sandpendel. 5 Nicht-Inertialsysteme 7 Nicht-Inertialsysteme Coriolis- / Zentrifugalbeschleunigung Sandpendel, Karussell ~a 0 = ~a + 2(~v 0 ⇥ ! ~) + ! ~ ⇥ (~r 0 ⇥ ! ~) W Abhängig von den Anfangsbedingungen und vom Verhältnis ⌦ : ! w S W w S' S' w w S 2r 60 a 0 60 wê2p = 0 wê2p = 1 wê2p = 2 wê2p = 3 40 L mg a s 20 rhs mw2R a HgradL 120 180 240 300 360 0 -20 -40 Im beschleunigten System : Scheinkäfte treten auf. -60 0 1 2 3 4 a HradL 5 6 Graphische Lösung findet die stabilen Winkel ↵. 6 8 Nicht-Inertialsysteme Zentrifugen Kapitel 6 Harmonische Schwingungen 9 Nicht-Inertialsysteme 11 Schwingungen Urananreicherung harmonisch Periodisch : feste Dauer zwischen wiederkehrenden ähnlichen oder gleichen Ereignissen. Harmonisch : die Zeitentwicklung einer Größe erfolgt gemäß einer Sinus- oder Cosinusfunktion. 10 12 Harmonische Schwingungen Harmonische Schwingungen Pendel z̈ + ! 2 z = 0 Schwingungsgleichung ! ! j komplexe Darstellung z = ce Lösungsansatz t d y>0 ksHz0-zL m S 2 Bestimmungsgleichung z0 z m F=mg 0 + !2 = 0 ! =± = i! 1 y<0 p 1! 2 = i! -mg z1 (t) = c1 ei ! t zwei Lösungen F " # mg z(t) = c1 ei ! t + c2 e Linearkombination beider mathematisches physikalisches und Federpendel z2 (t) = c2 i!t z(t) = C cos (!t + ') 13 Drehschwingung 15 Harmonische Schwingungen Position der Massen komplexe Darstellung m m r 8 imaginäre Achse T HsL 6 4 2 0 0 1 2 3 position 4 5 ”r y` r x+iy z⇤ = x z = x + iy ↵ = arctan iy y x a x` reelle Achse Polardarstellung 60 I = I0 + 2mr z = |z| ei ↵ 50 T 2 Hs2 L p 2⇡ T = = 2⇡ I/ ! 2 40 30 z ⇤ = |z| e i↵ 20 10 0 0 1 Anfitten einer quadratischen Funktion, Minimierung der Summe der quadratischen Abweichungen. 2 3 position 4 r 5 Eulersche Formel ⇡ I0 e±i↵ = cos ↵ ± i sin ↵ 14 16











