Komponenten - Uni Kassel

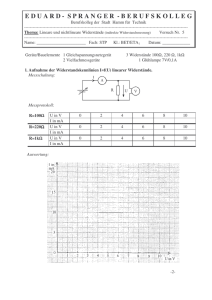
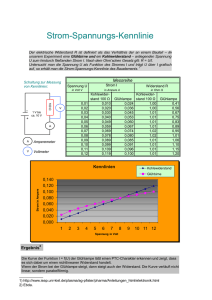
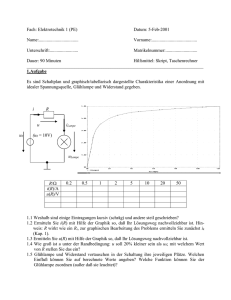
Fahrzeugsysteme und
Grundlagen der Elektrotechnik
Prof. Dr. rer. nat. L. Brabetz
Praktikum Fahrzeugsysteme
Versuchsunterlagen
Dirk Schneider
c Fachgebiet Fahrzeugsysteme und Grundlagen der Elektrotechnik
76
4
4.1
Messung/Modellierung an/von
Fahrzeugkomponenten
Einführung
Für Untersuchungen an größeren elektronischen Systemen wie dem Fahrzeugbordnetz werden vermehrt Simulationen eingesetzt. Hierbei müssen verschiedene zum Teil noch unbekannte
Verbraucher modelliert werden. Mit diesen Modellen können elektronische Lasten angesteuert
werden, die ihrerseits den Verbraucher im Bordnetz nachbilden.
Ziel dieses Versuchs ist es einen einfachen Verbraucher messtechnisch zu charakterisieren und
aus den resultierenden Daten ein Modell zu entwickeln, welches zur Ansteuerung einer elektronische Last geeignet ist. Anschließend ist das Modell anhand der aufgenommenen Messdaten
zu verifizieren und zu bewerten. In einem weiteren Schritt erfolgt die Ansteuerung einer elektronischen Last aus dem Modell heraus. Abschließend soll auch diese Emulation evaluiert werden.
4.1.1
Modelle
Bei der Modellierung ist zwischen zwei Verfahren zu unterscheiden:
Das physikalische Modell bildet die Funktion anhand der physikalische Formalismen ab. Hierbei sind die physikalischen Abhängigkeiten formal zu erfassen, die daraus resultierenden Differenzialgleichungen zu bilden und diese mit geeigneten Hilfsmitteln (z.B. MATLAB/Simulink)
zu lösen.
Einen weiteren Ansatz stellt die Nachbildung der Kennlinien durch Approximationsansätze dar.
Hierbei werden die Kennlinien durch P-I-D-Ansätze modelliert, wobei die Parameter über Optimierungsverfahren bestimmt werden.
4.1.2
Das physikalische Modell einer Glühlampe
In diesem Versuch soll ein physikalisches Modell einer Glühlampe entworfen werden. Hierzu
werden in diesem Abschnitt die physikalischen Gleichungen und Konstanten zum Erstellen
eines (vereinfachten) mathematischen Modells einer Glühlampe beschrieben.
Die Glühwendeln der heutigen Glühlampen bestehen fast ausschließlich aus Wolfram, weshalb
sich alle Variablen und Konstanten dieser Beschreibung mit Index W auf materialspezifische
Ergebnisse/Konstanten für Wolfram beziehen. In Tabelle 4.2 finden Sie alle nötigen Stoffkonstanten. Basis des Modells ist das Temperaturverhalten von Widerständen nach Gleichung 4.1.
77
4.1 Einführung
Metalle wie Wolfram zeigen hier ein klassisches PTC-Verhalten (Kaltleiter, positiver Temperaturkoeffizient).
RW = R20 · (1 + 4T · αW + 4T 2 · βW )
(4.1)
mit
∆T = TW − TU
[K]
(4.2)
folgt
RW = R20 · (1 + (TW − TU ) · αW + (TW − TU )2 · βW )
[Ω]
(4.3)
Das Problem in diesem Modell ist die Wolframtemperatur TW . Beim Einschalten erhitzt sich
die Glühwendel stark durch die aufgenommene elektrische Leistung und beginnt zu glühen, der
Widerstand steigt und das System pendelt sich im Wärmeaustausch mit der Umgebungstemperatur TU auf eine konstante Temperatur TW ein. Der Temperaturanstieg von TW kann mit den
folgenden Zusammenhängen in eine nichtlineare Differentialgleichung überführt werden.
Vereinfachend wird von direkter Wärmestrahlung in die Umgebungsluft nach dem Stefan-Boltzmann-Gesetz ausgegangen (Eigentlich ist der Glaskolben einer Glühlampe mit Schutzgas gefüllt. Es gibt einen Wärmeaustausch zwischen Glaskolben ↔ Umgebung, Glaskolben ↔ Schutzgas und Schutzgas ↔ Glühwendel).
Strahlungsleistung nach Stefan-Boltzmann:
P = σ · A · T4
[ W]
(4.4)
Beim Aufstellen der Gleichung für die Gesamtleistung ist darauf zu achten, dass die Glühwendel durch die elektrische Leistung und die Wärmestrahlung durch die Umgebungstemperatur
erhitzt wird und sich durch Abstrahlen der hohen Wolframtemperatur abkühlt.
Daraus ergibt sich die Wolframtemperatur TW :
TW =
Q
CW
Die Wärmemenge Q ist eine Energie, also gilt:
Z
Q = P dt
[ K]
(4.5)
[ Ws] = [ J]
(4.6)
Die Wärmekapazität CW lässt sich mit Hilfe der spezifischen Wärmekapazität von Wolfram cW
und der Masse des Glühdrates mW bestimmen:
CW = cW · mW
[
J
]
K
Damit kann die Differentialgleichung für TW aufgestellt werden.
(4.7)
78
4.1 Einführung
Tabelle 4.1: Daten zur Wendelgeometrie
Wolframdrahtdurchmesser dwo = 0, 08 mm = 8 · 10−5 m
Länge der Wendel
lwe = 5, 88 · 10−3 m
Wendeldurchmesser
dwe = 7, 4 · 10−4 m
Tabelle 4.2: Konstanten
Stefan-Boltzmann-Konstante:
σ = 5, 67 · 10−8 mW
2 K4
Dichte von Wolfram
kg
3 kg
%W = 19, 27 dm
3 = 19, 27 · 10 m3
J
J
spezifische Wärmekapazität von Wolfram cW = 0, 134 gK
= 134 kgK
2
spezifischer Widerstand von Wolfram
ρW = 0, 055 Ωmm
= 0, 055 · 10−6 Ωm
m
Temperaturbeiwert 1. Ordnung
1
αW = 4, 1 · 10−3 K
Temperaturbeiwert 2. Ordnung
βW = 1 · 10−6 K12
Wendelgeometrie
Wolframdraht
dwe
dwo
Iwo
lwe
Abbildung 4.1: Vereinfachte Wendelgeometrie
4.2 Vorbereitungen
4.2
79
Vorbereitungen
4.2.1
Allgemein
Bereiten Sie sich mit Hilfe der Einleitung, den Vorlesungsunterlagen und mit weiteren Quellen (Bibliothek, Internet) ausführlich vor. Sollten Fragen offen bleiben, wenden Sie sich bitte
rechtzeitig an einen Betreuer oder Herrn Haas, R. −1322.1, WA 73.
4.2.2
Fragen zur Vorbereitung
Beantworten Sie bitte zur Vorbereitung dieses Versuches schriftlich folgende Fragen: (Wählen
Sie allgemeine Ansätze. Die konkreten Werte ergeben sich während des Versuchs!)
1. Schätzen Sie für das endgültige Systemmodell die Wendelgeometrie ab. Man benötigt für
das Stefan-Boltzmann-Gesetz die Wendeloberfläche (Abstrahlfläche) und für die Masse
das Wolframvolumen. Der Widerstand R20 wird im Versuch gemessen. Erstellen Sie ein
m-File1 in dem die Wendeloberfläche, die Länge des Wolframdrahtes, der Wolframdrahtquerschnitt, das Wolframdrahtvolumen und die Masse des Drahtes in Abhängigkeit von
R20 und den gegebenen Konstanten berechnet werden.
2. Das Modell der Glühlampe basiert auf zwei Gleichungen. Die erste Gleichung ist die
Gleichung 4.3 zur Bestimmung von RW . Stellen Sie die zweite Gleichung zur Bestimmung von TW auf. Diese Gleichung ist eine Differentialgleichung (DGL). Welche Eigenschaften hat diese DGL?
4.3
4.3.1
Versuchsdurchführung
I/U-Kennlinie einer Glühlampe
Gegeben sind folgende Komponenten: Glühlampe, Quelle und zwei Multimeter.
Nehmen Sie zu Beginn der Messungen den Kaltwiderstand R20 der Glühlampe auf!
Es soll das Strom-/Spannungsverhalten der Glühlampe aufgenommen werden. Bauen Sie hierfür eine geeignete Schaltung auf. Beachten Sie die Größenordnung des Glühlampenwiderstands.
• Welche Fehler können sich ergeben? Bewerten Sie die Messkette.
1
Kann auch als Textdatei geschrieben werden, wenn Sie keinen Zugriff auf Matlab haben
4.3 Versuchsdurchführung
80
• Nehmen Sie die Kennlinie I = f (U ) auf.
Achten Sie auf die Erwärmung der Glühlampe. Schätzen Sie die Aufwärm- bzw. Abkühlzeit.
Was folgt hieraus für die Messung?
Wählen Sie bis zum Beginn des Glühens sehr kleine Messintervalle!
Werten Sie die Messung graphisch aus.
• Gibt es Auffälligkeiten im Kurvenverlauf? Wenn ja, wie sind diese zu erklären?
• Hat die Umgebungstemperatur einen Einfluss?
4.3.2
Einschaltverhalten einer Glühlampe
Gegeben sind folgende Komponenten:
• Glühlampe,
• Quelle,
• Oszilloskop,
• Stromzange für Oszilloskop (Fluke i310s) und
• Quecksilberschalter (Prellfrei).
Es soll das Einschaltverhalten der Glühlampe aufgenommen werden. Bauen Sie hierfür eine
geeignete Schaltung auf.
• Welche Fehler können sich ergeben? Bewerten Sie die Messkette.
• Welchen Einfluss hat das Oszilloskop bzw. die Quelle?
• Stellen Sie die Kennlinien von Strom I und Spannung U jeweils als Funktion der Zeit t
dar.
Werten Sie die Messung graphisch aus.
• Schätzen Sie die Einschwingzeit und den stationären Wert des Stromes mit Hilfe der
Messung ab.
• Bewertung Sie die Messung bezüglich Messfehlern und Dynamik. Berücksichtigen Sie
dabei insbesondere die Eigenschaften der verwendeten Geräte!
4.3 Versuchsdurchführung
4.3.3
81
Umsetzung des Modells einer Glühlampe in MATLAB/Simulink
Mit Hilfe des Softwaretools MATLAB/Simulink soll ein Modell der Glühlampe erstellt werden.
Hierzu ist das in der Vorbereitung entstandene Modell mit Simulink umzusetzen.
Vergleichen Sie Ihr Modell mit den Messergebnissen aus 4.3.1 und 4.3.2 hinsichtlich Kurvenform, Einschwingdauer und Endwert des Stromes. Was für Abweichungen ergeben sich und
wie sind diese zu erklären?
4.3.4
Steuerung einer elektronischen Last durch das
MATLAB/Simulink-Modell einer Glühlampe
Mit dem Real Time Windows Target Blockset lassen sich Signale über eine analoge I/O-Card
ein- und auslesen. Hierüber besteht die Möglichkeit eine elektronische Last anzusteuern und
die an ihr anliegenden Größen zurückzulesen. Die Integration eines vorgefertigten SubsystemBlocks (siehe Abbildung 4.2) in das Simulink-Modell ermöglicht die direkte Ansteuerung der
Abbildung 4.2: Vorgefertigter Simulink-Block zur Ansteuerung der elektronischen Last
elektronischen Last.
• Kopieren Sie die Blöcke Ihres kontinuierlichen Modells in das zeitdiskrete Modell mit
dem Subsystem-Block. Falls weitere Anpassungen notwendig sind, nehmen Sie diese
vor.
• Überprüfen Sie die Emulation durch eine vergleichende Messung mit Ihren zuvor gefundenen Ergebnissen in Abschnitt 4.3.2 (Messung mit Oszilloskop und Stromzange an der
Last).
• Welche Abweichungen ergeben sich und wie sind diese zu erklären?
• Inwieweit beeinflusst das Thema Echtzeit die gefundenen Ergebnisse?
Literatur
82
Literatur
[1] C LAUSERT, H. ; W IESEMANN, G. : Grundgebiete der Elektrotechnik 1. 8. Auflage. München, Wien : Oldenbourg, 2003
[2] T IETZE, U. ; S CHENK, C. : Halbleiter-Schaltungstechnik. 12. Auflage. Berlin : Springer,
2002
[3] S TÖCKER, H. (Hrsg.): Taschenbuch der Physik. 4. Auflage. Thun, Frankfurt am Main :
Verlag Harri Deutsch, 2000