ETP1_2 - HAW Hamburg

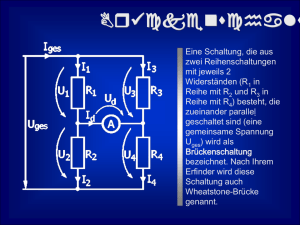
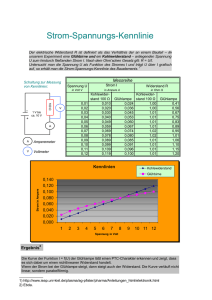
Department Informations- und
Labor für Grundlagen der
Elektrotechnik
Elektrotechnik
Studiengruppe:
Übungstag:
Professor:
Protokollführer (Name, Vorname):
ETP1-2
Weitere Übungsteilnehmer:
Testat:
Nichtlineare Kennlinien
Übersicht
Im ersten Teil dieser Laborübung soll die nichtlineare 𝐼-𝑈-Kennlinie einer Glühlampe errechnet und gemessen werden. Der zweite Teil beschäftigt sich mit einer Brückenschaltung und
deren Abgleichkennlinie. Die Kennlinien sind punktweise theoretisch und messtechnisch zu
bestimmen und grafisch darzustellen.
Theoretische Grundlagen





Bauelemente mit nichtlinarer 𝐼-𝑈-Kennlinie
Gleichstromwiderstand, differentieller Widerstand
Darstellung von Messergebnissen in linearer und logarithmischer Skalierungen
lineare Zweipolersatzschaltung eines nichtlinearen Bauelements
Theorie der Brückenschaltung, Brückengleichung
ETP1-2 / Version 1.3
1(3)
1 𝑰-𝑼-Kennlinie einer Glühlampe
Im Laborpraktikum wird als nichtlinerer Widerstand eine Glühlampe mit den Nenndaten
6𝑉 / 0,6𝑊 eingesetzt. Die bei der Gühlampe vorliegende nichtlineare Beziehung zwischen
Strom 𝐼 und angelegter Spannung 𝑈 lässt sich theoretisch in guter Näherung durch folgendes
Potenzgesetz beschreiben:
𝐼
𝑈 𝑏
= 𝑎 ⋅ (𝑉 )
𝑚𝐴
mit 𝑎 ≈ 40 und 𝑏 ≈ 0,5.
Dieser Sachverhalt soll durch Messung nachgewiesen werden.
1.1 Vorbereitungen
1.1.1 Berechnen Sie nach der obigen Gleichung den Glühlampenstrom als Funktion der
anliegenden Spannung, z.B. für 𝑈 = 0,1𝑉, 0,5𝑉, 0,8𝑉, 2,0𝑉, 5,0𝑉 und 6,0𝑉.
𝐼
𝑈
1.1.2 Zeichnen Sie mit den Ergebnissen ein Kennliniendiagramm 𝑚𝐴 = 𝑓(𝑉 ), in das Sie
später zum Vergleich auch die Messwerte eintragen können.
1.1.3 Stellt man die Kennlinie in doppelt-logarithmischem Maßstab dar, so ergibt sich eine
Gerade. Wie lassen sich daraus die Parameter 𝑎 und 𝑏 bestimmen?
1.2 Messungen
Durch gleichzeitige Strom- und Spannungsmessung ist die 𝐼-𝑈-Kennlinie der Glühlampe
punktweise zu bestimmen und grafisch darzustellen. Als Quelle benutzen Sie das Netzgerät
HM7042-5. Um den Spannungsbereich dieser Quelle voll auszuschöpfen, ist eine geignete
Messschaltung mit einem Spannungsteiler oder einem Vorwiderstand aufzubauen. Der genaue Aufbau muss aus dem Schaltplan hervorgehen.
1.2.1 Im Spannungsbereich von ca. 10𝑚𝑉 bis ca. 6𝑉 sind 𝑈 und 𝐼 zu messen und in einer
Tabelle festzuhalten (ca. 12 Messpunkte).
1.2.2 Tragen Sie Ihre Messpunkte in das vorausberechnete Diagramm ein und vergleichen
Sie die gemessenen Werte mit den theoretisch erwarteten.
1.2.3 Bestimmen Sie aus der Messung den Gleichstromwiderstand 𝑅𝐴 und den differentiellen
Widerstand 𝑟𝑑 bei den Spannungen 𝑈 = 0,5𝑉, 2,0𝑉 und 5,0𝑉.
Tragen Sie die Ergebnisse in eine Tabelle ein.
1.2.4 Stellen Sie die theoretische Kennlinie 𝐼 = 𝑓(𝑈) und Ihre Messwerte auf doppeltlogarithmischem Papier dar. Legen Sie eine Ausgleichsgerade durch die Messpunkte.
Überprüfen Sie die Gültigkeit der obigen Formel im unteren und oberen
Spannungsbereich.
ETP1-2 / Version 1.3
2(3)
1.2.5 Bestimmen Sie die Parameter 𝑎 und 𝑏 anhand einer Ausgleichsgeraden aus dem
Diagramm.
1.2.6 Ab welchen Strömen aufwärts verhält sich die Glühlampe annähernd linear?
Geben Sie die für diesen Bereich gültige Ersatzzweipolquelle an (Schaltung und
Werte).
2 Brückenschaltung
In der gezeigten Brückenschaltung kann die Brückenspannung 𝑈𝑎𝑏 mit dem Potentiometer 𝑅1 zu Null abgeglichen werden.
Für den Schaltungsaufbau sind zu wählen :
R3
R1
b
UB
𝑅2 = 1,0𝑘Ω, 𝑅3 = 𝑅4 = 10,0𝑘Ω,
𝑈𝐵 = 6,0𝑉 (Netzgerät HM7042-5)
R2
V
Uab
a
R4
Für 𝑅1 ist eine Widerstandsdekade zu verwenden.
2.1 Vorbereitungen
2.1.1 Berechnen Sie (alternativ: simulieren Sie mit PSpice) die Brückenspannung 𝑈𝑎𝑏 als
Funktion von 𝑅1 für 𝑅1 = 600Ω … 1800Ω in 200Ω-Schritten. Stellen Sie die
Wertepaare grafisch in folgendem Maßstab dar:
𝑈𝑎𝑏 (Ordinate): 100𝑚𝑉/𝑐𝑚, 𝑅1 (Abszisse): 100Ω/𝑐𝑚.
2.1.2 Bestimmen Sie den Wert von 𝑅1 , bei dem die Brücke abgeglichen ist.
Dies sei der Wert 𝑅10 .
2.2 Messungen
2.2.1 Bauen Sie die Brücke gemäß der obigen Schaltung auf. Benutzen Sie für den variablen
Widerstand 𝑅1 eine Widerstandsdekade. Messen Sie zunächst den Wert von 𝑅1 , bei
dem die Brücke abgeglichen ist. Ist dieser gleich dem theoretisch berechneten 𝑅10 ?
2.2.2 Messen Sie die Brückenspannung als Funktion von 𝑅1 für
𝑅1 = 500Ω, 750Ω, 1𝑘Ω, 1,25𝑘Ω, 1,5𝑘Ω und 2,0 𝑘Ω.
2.2.3 Halten Sie die Messwerte und die relative Verstimmung 𝑣 =
fest.
𝑅1 −𝑅10
𝑅10
in einer Tabelle
2.2.4 Stellen Sie die Funktion 𝑈𝑎𝑏 = 𝑓(𝑅1 ) grafisch dar und vergleichen Sie die Messwerte
mit dem theoretisch erwarteten Verlauf.
2.2.5 Konstruieren Sie die Tangente im Abgleichpunkt und bestimmen Sie die
Δ𝑈
Empfindlichkeit 𝐸0 = Δ𝑅𝑎𝑏 des Brückenabgleichs.
1
ETP1-2 / Version 1.3
3(3)