¨Ubungen zur Vorlesung Einführung in die Physik für Natur
Werbung

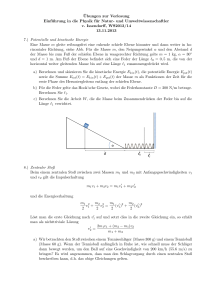
Übungen zur Vorlesung Einführung in die Physik für Natur- und Umweltwissenschaftler WS2015/16 v.Issendorff 11.11.2015 5.) Achterbahn a) Eine Achterbahn fährt in einen Looping mit 10 m Durchmesser ein. Wie schnell muss die Bahn am höchsten Punkt des Looping sein, damit ein Passagier der Masse m noch mit einer Kraft von F = 0.5 mg in seinen Sitz gepresst wird? b) Wenn es sich um einen Mehrfach-Looping handelt: wie groß ist dann die Geschwindigkeit der Bahn am tiefsten Punkt des Looping, wie groß ist hier die scheinbare Schwerebeschleunigung? (d.h. welche Kraft wirkt hier auf die Passagiere?). Beachten Sie, dass die Bahn am höchstem und tiefsten Punkt eine unterschiedliche potentielle Energie hat, und dass sich tatsächliche Schwerebeschleunigung und Zentrifugalbeschleunigung an den beiden Punkten unterschiedlich addieren (sie sind einmal entgegengesetzt gerichtet, einmal parallel) c) Nun fahre die Achterbahn (Masse 500 kg) eine schiefe Ebene (Höhe 30 m, waagerechte Länge 60 m) herunter (sie sei anfänglich in Ruhe). Berechnen Sie den zeitlichen Verlauf der potentiellen und der kinetischen Energie und skizzieren Sie diese. 6.) Tennis Beim einem zentralen Stoß zwischen zwei Massen m1 und m2 mit Anfangsgeschwindigkeiten v1 und v2 gilt die Impulserhaltung m1 v1 + m2 v2 = m1 v10 + m2 v20 und die Energieerhaltung m1 2 m2 2 m1 0 2 m2 0 2 v + v = (v ) + (v ) 2 1 2 2 2 1 2 2 Löst man die erste Gleichung nach v10 auf und setzt dies in die zweite Gleichung ein, so erhält man als nichttriviale Lösung v20 = 2m1 v1 + (m2 − m1 )v2 m1 + m2 a) Wir betrachten den Stoß zwischen einem Tennisschläger (Masse 300 g) und einem Tennisball (Masse 60 g). Wenn der Tennisball anfänglich in Ruhe ist, wie schnell muss der Schläger dann bewegt werden, um den Ball auf eine Geschwindigkeit von 200 km/h (55.6 m/s) zu bringen? Es wird angenommen, dass man den Schlagvorgang durch einen zentralen Stoß beschreiben kann, d.h. das obige Gleichungen gelten. b) Nun kommt der Ball mit 100 km/h (27.8 m/s) angeflogen, und der Schläger wird locker in die Flugbahn gehalten (also ruhend). Wie sind die Geschwindigkeiten von Schläger und Ball nach dem ”Stoß ”? (Sie können für beide obige Formel verwenden, wenn Sie einmal den Ball und einmal den Schläger als Masse 2 ansehen) c) Wie schnell muss der Schläger bewegt werden, damit nach dem Schlag ein mit 100 km/h anfliegender Ball mit der gleichen Geschwindigkeit zurückfliegt?