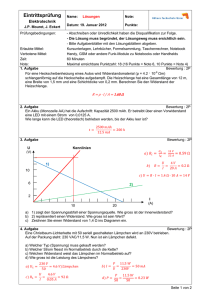
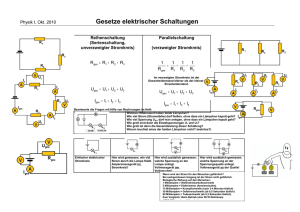
1.Übertragung elektrischer Energie
Werbung

1.Übertragung elektrischer Energie 1.1. Modellexperiment für die Verlustleistung Materialien: - gelber Netzwürfel (6V bzw. 12V) - Steckbrett - Lämpchen (6V, 500mA) - Widerstand 100 - 3 schwarze Kabel Aufbau: Durchführung: Zuerst wird das Lämpchen ohne den Widerstand betrieben Lämpchen leuchtet Große Entfernung entspricht großen Widerstand in den Leitungen Widerstand symbolisiert die „lange Leitung“, in der Spannung abfällt. Schaltet man nun den Widerstand dazu, leuchtet das Lämpchen nicht mehr die Leitung hat uns zu viel Leistung gekostet (Verlustleistung) Ohne Widerstand: PLämpchen U I 6V 500mA 3W RLämpchen U 6V 12 I 0,5 A Mit Widerstand: Reihenschaltung: I = konst., UGesamt 6V U Lämpchen U Leitung U Lämpchen U Leitung U Lämpchen 6V U Lämpchen I I Lämpchen U Lämpchen RLämpchen RLämpchen RLeitung 12 0,12 100 U Lämpchen 0,64V 0, 64V 0, 053 A 12 Verlustleistung: PLeitung I RLeitung (0,053 A) 100 0,3W 2 2 (Stromstärke ist für Erwärmung der Kabel verantwortlich) Wirkungsgrad: PLämpchen PLämpchen PLeitung PLämpchen PGesamt UL IL UG IG I konst . U L 0, 64V 0,11 UG 6V 1.2. Verbesserte Verlustleistung Materialien (zusätzlich): - 2 Weicheisenkerne mit T-Stück 2 Spulen mit N=600 und 2 Spulen mit N=75 Aufbau: Durchführung: Einbau von 2 Transformatoren, 1 nach Kraftwerk zum Hochtransformieren der Spannung (kleine Windungszahl bei Primärstromkreis (also direkt an Spannungsquelle)) ( also wird die Stromstärke I kleiner), 1 vor Verbraucher zum Runtertransformieren der Spannung (genau umgekehrt) (siehe extra Foto) 2 Netzschalter umlegen Lämpchen leuchtet jetzt die Verlustleistung P I R muss also jetzt wesentlich geringer sein Erklärung: Warum muss die Spannung in den Hochspannungsleitungen z.B. 120kV – 180KV betragen und nicht wesentlich weniger? - höhere Spannungen nicht möglich zwecks Funkenüberschlag (wegen kapazitiven Widerstand zwischen Hin- und Rückleitung) - Ermittlung des Energieaufwands der Verbraucher (also Leistung) und Bestimmung der maximalen Stromstärke aus Leitungseigenschaften (Dicke der Leitungen nicht unendlich) um die maximale Spannung in den Leitungen zu bestimmen - P in Reihenschaltungen wird mit I 2 * R (nicht ) I muss runtertransformiert werden, also U rauf. Zusatzinfo: 3 Arten von Widerständen: induktiver (bei Spulen), kapazitiver (bei Kondensatoren) und ohmscher Widerstand Runtertransformation der Spannung in mehreren Teilschritten Trafogesetz: N1 U1 I 2 N 2 U 2 I1 2. Wirkungsgrad eines E-Motors (9.Klasse) WICHTIG: Vor jeder Messung Leistungsmessgerät zeitgleich auf „reset“ stellen, Zeitmessung startet nämlich sofort! Alternativ mit Stoppuhr durchführen. Materialien: E-Motor (Schrank 19 im kleinen Seminarraum) 2 Klemmen, um E-Motor am Tisch festzuklammern Leistungsmessgerät (14.1) 2 Gewichte (z.B. 2kg und 5kg) Lineal evtl. Styropor unterlegen Zum E-Motor: Stromschalter des E-Motors in Leistungsmessgerät einstecken Linker Schalter ist Drehrichtung, rechter Schalter An/Aus 2.1. Messen der Leistungsaufnahme (oft in Prüfung nicht verlangt) Aufbau: Durchführung: Leistungsmessgerät auf „W“ Die 2 verschiedenen Gewichte mit 2 verschiedenen Geschwindigkeiten hochziehen lassen (hoch, da Wirkungsgrad bestimmt wird, indem man der Schwerkraft entgegen wirkt). Geschwindigkeit Gewicht 2kg 5kg 3 45 W 45 W 6 55 W 58 W Aufgenommene Leistung - unabhängig vom Gewicht (nur, da Wirkungsgrad des E-Motors so schlecht ist: Anzeige ist fast ausschließlich getriebebedingt) abhängig von der Geschwindigkeit 2.2. Wirkungsgrad des E-Motors Aufbau: Zusätzlich Lineal auf Stativ aufbauen Leistungsmessgerät auf „Ws“ (somit benötigt man keine Stoppuhr) Durchführung: Berechnung des Wirkungsgrads über: Pab Wab m g h Pauf Wauf Pauf t (aus Messwerten) (abgelesen) 2kg, Geschwindigkeit 3: m g h P t m g h 2kg, Geschwindigkeit 6: P t m g h 5kg, Geschwindigkeit 3: P t 5kg, Geschwindigkeit 6: m g h P t m 0,52m s2 2,3% 452 J 2kg 9,81 m 0,52m s2 3, 25% 320 J 2kg 9,81 m 0, 44m s2 5,3% 405 J 5kg 9,81 m 0,38m s2 7,3% 256 J 5kg 9,81 Je größer die Geschwindigkeit, desto größer der Wirkungsgrad Je größer das Gewicht, desto größer der Wirkungsgrad Beispiele für Wirkungsgrad: Dieselmotor 40 45% Ottomotor max. 40% E Motor 90% Solarzelle 15 20% 3. Kennlinien elektrischer Bauteile 3.1. Qualitativer und quantitativer Versuch Materialien: - graues Leistungsnetzgerät - 1m Eisendraht (d=0,2mm, 4 - 2 Isolierstützen GROßES Ampere- und Voltmeter ) m Aufbau: Durchführung: Qualitativ: Beim Hochdrehen der Spannung schlagen sowohl das Ampere- als auch das Voltmeter „gleichmäßig“ aus. Ab einer bestimmten Spannung (bei uns 5V) erkennt man, dass die Amperemeter-Anzeige „zurückhängt“, d.h. ab dem Bereich, ab dem der Draht wärmt wird, steigt das Voltmeter gleich schnell weiter, während die Anzeige des Amperemeters langsamer wird. Quantitativ: Aufnahme der U-I-Werte in Tabelle Graph zeichnen Dieser zeigt die Nicht-Linearität der U-I-Kennlinie des Eisendrahtes. Eventueller Zusatzversuch: „Zeigen Sie, dass sich der Widerstand eines Drahtes mit der Temperatur ändert“. Materialien (zusätzlich): - Lämpchen (1,5V, 0,15A) Bunsenbrenner Aufbau: Durchführung: - Draht um einen Stift so eng wie möglich wickeln, um das Erhitzen zu erleichtern - Spannung am Netzgerät so einstellen, dass Lämpchen leuchtet - mit Bunsenbrenner Draht gleichmäßig erhitzen Lämpchen leuchtet deutlich dunkler und geht sogar fast aus Erklärung: Widerstand des Drahtes wird bei höherer Temperatur größer Strom wird kleiner ( R 3.2. U-I-Kennlinie mit x-y-Schreiber Materialien: - x-y-Schreiber (im kleinen Praktikumsraum) schwarzes Netzgerät (15.3) Steckbrett mit Kabeln Lämpchen (7V, 0,1A) Widerstand 22 (von Hr. Lohner) Aufbau: U ) I x-Eingang: parallel zum Lämpchen: gemessen wird die Spannung am Lämpchen y-Eingang: parallel zum Widerstand: gemessen wird die Spannung am Widerstand, die aber wegen R=konst. proportional zur Stromstärke ist. Wegen der Reihenschaltung von Widerstand und Lämpchen wird also auf der y-Achse die Stromstärke vom Lämpchen aufgetragen. Durchführung: Zum x-y-Schreiber: - „Range“ ganz nach rechts drehen - Tasten „Pen Offset“ bewegen den Stift nach rechts/links bzw. oben/unten Zeichnen der Koordinatenachsen - Schalter „Pen Off/Down“ ganz rechts Stift nach oben bzw. unten stellen - Einstellungen: x-Achse und y-Achse: 0-25 V/cm - Prüfe die Einstellungen: Stift oben und Probedurchgang durchführen Versuch: - Strombegrenzung maximal im Netzgerät (rechtes Rad auf max. stellen) - Stift des x-y-Schreibers mit „Pen Down“ nach unten - gleichmäßiges Aufdrehen und Zurückdrehen! der Spannung führt zum Graphen Erklärung: Graph beim Aufdrehen Graph beim Zurückdrehen Graph beim Aufdrehen: Der eigentliche Widerstand des Lämpchens (Wolframdraht) (der mit den Daten der Lampe berechnet werden kann) wird als „Warmwiderstand“ bezeichnet. Dieser wird erst ab einer bestimmten Temperatur erreicht. Vor dieser Temperatur wird der Widerstand des Lämpchens als „Kaltwiderstand“ bezeichnet, dieser ist wesentlich niedriger als der Warmwiderstand. Daher fließt beim Einschaltvorgang schon bei geringer Spannung sehr viel Strom. Beim Aufdrehen der Spannung geht dann der Kaltwiderstand in den Warmwiderstand über. Graph beim Zurückdrehen: Die Abkühlung des Drahts erfolgt nicht schlagartig, geht langsam zurück (Wärmeaustausch mit der Umgebung) Sonstiges: PTC: Positiver Temperaturkoeffizient: Der Widerstand steigt mit zunehmender Temperatur (z.B. Wolframdraht und Eisendraht) NTC: Negativer Temperaturkoeffizient: Widerstand steigt mit abnehmender Temperatur Farbige Kabel zwecks Polarität (z.B. Kohle) Mischpotential hat niedrigeres Pot. als „rotes“ Pot. Mischpotential Mischpotential hat höheres Potential als „blaues Potential“ Bsp.: Glühbirne geht wenn dann beim Einschalten kaputt 3.3. U-I-Kennlinie mit Oszillographenbildschirm Materialien: - Oszillograph mit speziellen Oszi-Kabeln Frequenzgenerator Steckbrett Widerstand 100 Diode BY103 Aufbau: Einstellungen: Frequenzgenerator: - 200Hz - Mode Sinusfrequenz (linke Taste) - Attenuator: 0 - Amplitude voll aufdrehen nach rechts Oszillator: - B Time / Div: egal - A Time / Div: xy (keine Zeitauflösung) (voll aufdrehen) - Position x: Graph rechts/links - Position y: rausziehen (spiegelt y-Richtung) - Trigger: Norm und Kanal 1 - Vertikal: DC, Kanal 1, Pul Inf (je nach beliebigen y-Achse umdrehen) Wissen: Auslesen der Zündspannung: Volt / Div in x- Eingang verstellen zum Strecken des Graphen Kennlinie zum besseren Ablesen ins Zentrum verschieben Kennlinie steigt leicht an bis zur Zündspannung, Spannung schlägt dann durch Aufnahme der Kennlinie erfolgt bei uns in Durchlassrichtung der Diode. Um in Sperrrichtung eine Kennlinie aufzunehmen, benötigt man eine Zener-Diode. Dioden nochmal nachlesen!!! Zehnerdiode wird immer in Sperrrichtung verwendet, um konstante Spannungsschwankungen zu erhalten (z.B. Schwankungen von 1 V um einen Wert von Bsp. 12 V (d.h. 13 – 11 Volt) zu erreichen ´Normale´ Diode in Sperrrichtung brennt durch und ist zerstört. Die Sperrschicht wird zuerst ausgedehnt und erst bei hohen Spannungen schlagen die Elektronen durch. 4. Innenwiderstand von Stromquellen 4.1. Ausgangsspannung einer Batterie ist geringer als die Leerlaufspannung Materialien: - 9 V Batterie - Lämpchen (6 V, 0,5 A) - Voltmeter Aufbau: Leerlaufspannung Ausgangsspannung Durchführung: Die Leerlaufspannung einer Batterie wird ohne Verbraucher gemessen, ihre Ausgangsspannung mit einem Lämpchen als Verbraucher man sieht: Ausgangsspannung < Leerlaufspannung Erklärung: Es handelt sich um eine Reihenschaltung aus Innenwiderstand der Batterie und dem Widerstand des Lämpchens. Am Innenwiderstand RI fällt jedoch ein gewisser Teil der Spannung ab. Umso größer der Widerstand des Verbrauchers, desto mehr Spannung fällt an diesem ab. 4.2. Innenwiderstand einer 9V-Batterie U 0 8, 46V , U Kl 6V RLampe U Kl U Kl 2 (6V )2 7, 2 I P 5W Aufgrund der Reihenschaltung ist I = konstant: RInnenwiders tan d U i U 0 U Kl U 0 U Kl U Kl I I RLampe RInnenwiders tan d RLampe (U 0 U Kl ) U Kl 7, 2(8, 46V 6V ) 3 6V Gäbe es Spannungsquellen ohne Innenwiderstand, so würden sie nach der U Widerstandsdefinition I bei Kurzschluss unendlich hohe Stromstärke liefern, wofür R unendlich viel Energie nötig wäre ( P U I ). Batterien und Netzgeräte haben deshalb immer Innenwiderstände. Das beeinflusst allerdings die erzeugte Klemmenspannung U Kl , denn der Spannungsabfall am inneren Widerstand reduziert (je nach Stromstärke mehr oder weniger) die ursprüngliche Quellenspannung U 0 : U Kl U 0 RI I 5. Generator: Darstellung der Generatorspannung auf dem Oszilloskop: Elektromotor 5.1. Modellversuch zur Funktion eines Generators Materialien: - Hufeisenmagnet Spule in Modell (12.3) Riemen (28.3 im Schrank im Gang) Lämpchen 6V, 50mA Tischklemmen SCHWARZE Kabel, da Wechselspannung erzeugt wird (auf Foto falsch) Aufbau: Durchführung: Kurbeln führt zu induziertem Strom, der zu flackerndem Leuchten des Lämpchens führt (Indiz auf die Wechselspannung, die man mit dem Generator erzeugt) Wissen: Ein Generator besteht aus Rotor und Stator (hier: T-Anker im Magnetfeld). Im Generator werden eine Spule und ein Magnet so gegeneinander bewegt, dass durch Induktion eine Wechselspannung entsteht: Lenzsche Regel: Der induzierte Strom fließt immer so, dass er der Bewegung, durch die er entstanden ist, entgegenwirkt. Der Betrag der Induktionsspannung hängt von der Geschwindigkeit der Änderung des Magnetfelds ab. EVTL LEIFI: in welcher Position wird Spannung induziert Für die Induktionsspannug gilt: U ind B dA , also wichtig ist die Flächenänderung pro Zeit, nicht dt die Größe der durchsetzten Fläche! Bsp.: In der Spulenstellung des obigen Bildes wird zwar die maximale Fläche der Spule durchsetzt, die induzierte Spannung ist jedoch gleich Null, da man dort die kleinste Flächenänderung pro Zeit erreicht. Der Stator kann ein Dauermagnet oder Elektromagnet sein. Er besitzt ein magnetisches Feld, das im Raum zwischen den beiden Polen des Magneten vorhanden ist und damit auch die Leiterschleife durchsetzt. Der Rotor ist eine Leiterschleifer oder Spule, die über eine Welle angetrieben wird und die damit im Magnetfeld des Stators rotiert. Durch die Rotation ändert sich das von der Spule umfasste Magnetfeld. 5.2. Wechselspannung auf Oszillographen zeigen Zusätzliche Materialien: Oszillator mit Oszi-Kabel Aufbau: Einstellung am Oszi: - Kabel an y-Eingang, AC (Wechselspannung) einstellen B Time / Div: egal A Time / Div: xy (keine Zeitauflösung) (voll aufdrehen) Trigger: Auto und Kanal 2 Vertikal: Kanal 2, AC Durchführung: Achte darauf, dass die Schleifringe guten Kontakt zu den Kohlebürsten haben - Schleifringe am Generator einstellen: einer ganz innen, die andere Seite am mittleren Ring (also ohne Kommutator) Erzeugung sinusförmiger Wechselspannung Oszillator auf xy (keine Zeitauflösung) stellen und kurbeln und evtl. A Time/Div und Volts/Div ändern senkrechte Linie Zeitauflösung auf ungefähr 20ms stellen und kurbeln sinusförmige Wechselspannung: Taste „Storage“ macht Bild langsam, „Hold“ zum endgültigen Einfrieren des Bildes 5.3. Pulsierende Gleichspannung Änderungen zum vorherigen Versuchsteil: Schleifkontakte umstellen: Beide ganz außen, also auf den Kommutator. Oszi auf DC (Gleichspannung) umstellen pulsierende Gleichspannung 5.4. Generator als Gleichspannungsmotor Zusätzliche Materialien: - schwarzes Netzgerät (15.3) mit 10V blaues und rotes Kabel Aufbau: Durchführung: - Spannung auf 10 V aufdrehen - Spule leicht mit Finger anstupsen Spule dreht sich automatisch Wissen: Ein Gleichstrommotor dient zur Umwandlung von elektrischer Energie in Bewegungsenergie (praktisch die andere Richtung der bisherigen Versuche). Ursache: bewegte Ladung in der Spule Bei senkrechter Stellung der Leiterschleife ist die Gesamtkraft 0. Die Leiterschleife bewegt sich aber aufgrund ihrer Trägheit weiter. Zugleich wird in dieser Stellung durch den Kommutator (Polwender) dafür gesorgt, dass der Strom in der Leiterschleife seine Richtung ändert. Er wirkt so, dass die Drehbewegung in der gleichen Richtung fortgesetzt wird. Dieser Vorgang wiederholt sich ständig. 6. Gebäude und Personenschutz 6.1. Gefährdung und Schutz der Hausinstallation bei Überlast und Kurzschluss Materialien: - grauer Leistungsnetzwürfel (15.3) rote und blaue Kabel (da Gleichspannung) 4 Lämpchen 12V / 50W 5cm (muss kurz sein wie in der Realität) Kupferdraht 0,2mm 2 dünne Kabel = Hausleitung (von Herr Lohner) 3 Isolierhalter (um den Draht einklemmen) Aufbau & Durchführung: Strombegrenzung fast auf Maximum einstellen Lämpchen nimmt sich eh nur die Stromstärke, die es benötigt a) Geräteschutz mit Schmelzsicherung 1. Schritt: Aufbau ohne Sicherung (siehe Fotos mit Sicherungsdraht) 12V am Leistungsgerät (Strombegrenzung auf Maximum, da sich der Strom dem Verbraucher anpasst) mit nur 1 Lämpchen im Stromkreis Parallelschalten zusätzlicher Lämpchen während das Gerät angeschaltet bleibt Draht wird warm (erfühlen) beim 4 Lämpchen raucht das Kabel: lange eingeschaltet lassen, damit der Schüler was sieht! 2. Schritt: Aufbau mit Sicherung Einbauen des Kupferdrahts 12V am Leistungsgerät mit nur 1 Lämpchen im Stromkreis Parallelschalten des 2. Lämpchens Sicherungsdraht glüht rot Parallelschalten des 3. Lämpchens Sicherungsdraht schmort durch Nützliches: Lohner: Denkt z.B. an Computer, bei dem oft Mehrfachsteckdosen verwendet werden. Bei billigen Mehrfachsteckdosen ist der Draht minderwertig / dünn Durchbrenngefahr Spätestens beim 3. Lämpchen soll die Sicherung fliegen, da hier die Erwärmung des Kabels beginnen würde Physikalisch: Parallelschaltung: UGes U1 U 2 U3 1 1 1 1 durchs Parallelschalten der Lämpchen: RGes wird kleiner I wird R Ges R 1 R 2 R 3 größer Draht schmort durch Anwendung: Schmelzsicherungen noch im Auto, Sicherungskasten (allerdings mit Thermoschalter) b) Geräteschutz mit Kurzschluss Fast gleicher Versuchsaufbau, nur noch 1 Lämpchen 1. Schritt: Lämpchen kurzschließen Leitung raucht sofort 2. Schritt: Sicherung einbauen, Lämpchen wieder kurzschließen Sicherungsdraht brennt durch Kurzschluss in Nahaufnahme: 6.2. Personenschutz Materialien: - Steckbrett Personenschutz (16.3) Schwarze Kabel Theorie, die man dazu wissen MUSS: Funktionsweise des FI-Schalters (Fehlerstromschutzschalter): - FI-Schalter ist ein Schutzschalter, der selbsttätig auslöst, wenn ein Fehlerstrom fließt, der größer ist als der Nenn-Fehlerstrom des Schutzschalters Fehlerstrom IFEHL = Iphase – Inull Schalter misst die Differenz zwischen Strom hinführender Leitung (Phasenleiter) und Strom rückführender Leitung (Nullleiter) Nur indirekter Schutz für den Menschen, da FI-Schalter schon auslösen soll, wenn Isolationsschaden auftritt und nicht erst, wenn der Mensch das Gerät berührt. Löst nur aus, wenn Stromstärke > 30 mA (Fehlerstrom) über die Erde abließt, Stromstärke auf FI-Schalter ablesbar. Übergangswiderstand zur Erde darf nicht größer als 1,6 kOhm = 50V/30mA (50 V als Grenzspannung und 30 mA als Grenzstromstärke für den Menschen festgesetzt) Allgemeines zur Hausinstallation: - - Es gibt generell 3 Phasen, 1 Phase würde prinzipiell ausreichen, aber vom Kraftwerk mehr Phasen geliefert, damit nicht alle Steckdosen / große Geräte / Licht etc. auf einer Phase laufen Erdstrom: Strom, der zur Erde abfließt - - - Kraftwerk geerdet, aber Potentialunterschied zwischen Erde des Kraftwerks und der Erde des Haushalts Fundamenterder: Ring ums Haus unter der Erde, muss Widerstand von 1,6 kOhm haben, auf keinen Fall größer. Ein Fundamenterder ist ein unisolierter elektrischer Leiter, der in ein Betonfundament eingebettet ist und zum Zweck der Erdung eine elektrisch gut leitende Verbindung zum Erdreich herstellt Potentialausgleichsschiene: hier sind alle Schutzleitungen angeschlossen. Die Potentialausgleichsschiene legt alle über sie miteinander verbundenen metallenen Strukturen und Einrichtungen eines Gebäudes sowie den Fundamenterder auf ein gemeinsames Erdpotential. Erde des Hauses ist durch Fundamenterder und Potentialausgleichsschiene im Zählerkasten geerdet Zwischen Phase und Nullleiter besteht Spannungsunterschied von 230 V, ebenso zwischen Phase und Schutzleiter Berührspannung = Spannung, die ein Körper bei Berührung mit einem leitenden Körper „abkriegt“ Stromfluss durch den Körper Durch eine beschädigte Isolierung kann das Gehäuse eines Betriebsmittels Spannung gegen den nächsten Erdpunkt annehmen, z.B. gegen Erde oder gegen geerdete Teile (z.B. Wasserleitungen) Eine solche Spannung nennt man Fehlerspannung oder auch Berührspannung. Die Berührspannung ist die Spannung, die zwischen gleichzeitig berührbaren Teilen während eines Isolationsfehlers auftreten kann. Die Grenze für die dauernd zulässige Berührspannung ist international vereinbart (Tabelle). Sie ist für Menschen und Tiere nicht lebensbedrohlich. für Menschen Wechselspannung (AC):50V, Gleichspannung (DC): 120V Durchführung: a) Mit Schutzleiter (gelb-grünes Kabel): - - Nullleiter Steckdose – Nullleiter Licht (blaues Kabel) Phasenleiter (Außenleiter) Steckdose - Phasenleiter (Außenleiter) Licht (schwarzes Kabel) Bei ordnungsgemäßem Anschluss durch Elektriker: Schutzleiter Steckdose – Schutzleiter Licht (gelb-grünes Kabel) Isolationsschaden im Gerät, demonstriert durch Entweder Überbrückung von Phasenleitung und Schutzleitung im Gerät durch Steckverbindung Oder gleichbedeutend und zum Demonstrieren schöner: Phasenkabel (schwarz) mit elektrisch leitendem Gehäuse (bei Demogerät einfach nur hinlegen, aber auf Berührung mit Metall achten) Beobachtung: FI-Schalter löst sofort aus, da Strom über den Schutzleiter zur Erde abfließt Differenz ungleich Null zwischen Außenleiter und Nullleiter im FI-Schalter b) Ohne Schutzleiter: - Zuerst Mensch erden, sonst funktionierts nicht! - Überbrückung im Gerät stecken lassen, da es der Situation „Ladungen sind auf dem Gerät“ entspricht. FI-Schalter löst NICHT aus, wenn Schutzleiter von Steckdose und Licht nicht verbunden ist (Installationsfehler! Wirkung des FI-Schalter in dem Fall nutzlos), sondern löst erst bei Berührung des defekten Gerätes durch den Menschen aus, weil erst hier Strom zur Erde abfließt. c) Ohne FI-Schalter: Mit Kasterl FI-Schalter überbrücken Mensch bei Berührung mit elektrisch leitender Oberfläche sofort tot d) Sonstiges - - M – N Potential des Nullleiters und des Menschen stimmen überein kein Stromfluss keine Gefährdung für den Menschen M – PE überhaupt keine Gefährdung des Menschen, da Schutzleiter geerdet M – L Stromfluss, da Potentialunterschied rote Lampe leuchtet auf (Gefährdung des Menschen) Mit Phasenprüfer (1.3) kann überprüft werden, welche Phase wo in der Steckdose ist: Finger auf Kontakt oben am Stift halten Phasenprüfer leuchtet nur auf, wenn Sensor auf Leiter (Phase) ist, das andere „Loch“ ist der Nullleiter. Seitlich an der Steckdose befindet sich der Schutzleiter. 7. Belasteter und unbelasteter Transformator 7.1a) Transformator mit Gleichstromquelle Durchführung: Transformator an Gleichstromquelle anschließen. Lämpchen leuchtet nicht. Dann Wechselstromquelle verwenden (gleiche Spannung, gleiche Stromstärke). Lämpchen leuchtet. Erklärung: Wegen des Gleichstroms erfolgt keine Änderung der Stromrichtung in der Spule. Deshalb auch keine Änderung des magnetischen Feldes, was für die Induktion der elektrischen Spannung erforderlich wäre. 7.1.b) Zusammenhang primärseitiger zu sekundärseitiger Leistungsaufnahme Durchführung: Unbelasteten Transformator betreiben. U und I messen. Dann Transformator mit verschiedenen Lämpchen (mehreren) belasten. U und I sowohl im primären als auch im sekundären Stromkreis messen. Ergebnis: PP = PS Erklärung: PP = UP * IP = n * UP * * IP = US * IS = PS 7.1c) Zusammenhang zwischen Spannung und Windungszahl beim unbelasteten Transformator Modelltransformator Materialien: - Gelbes Netzteil (6V) Lämpchen (6V, 3W) Spulen: 2xN=300, N=600, N=900, N=1200 2 Multimeter - Eisenkern mit Joch Aufbau: Durchführung: Verschiedene Spulenkombinationen mit Primärspule N=300 Spannung an Primär- und Sekundärspule messen und in eine Tabelle eintragen Ergebnis: N1 U1 N2 U 2 Primärspule mit einer Windung: N p 1 Wenn N s 1 , dann ist U ind U p . Für N s 2 hat man wieder pro Windung U ind U p , also insgesamt U ind 2 U p (Reihenschaltung) Bei n Windungen U ind n U p Wissen: Sekundärspannung wegen Feldverlusten oftmals etwas geringer. Funktionsprinzip eines Trafos: Wechselspannung Up Wechselstrom Ip magnetisches Wechselfeld in Spule, das durch Eisenkern verstärkt wird und zur Sekundärspule hindurchgeführt wird Induktionsspannung Us in Sekundärspule Primärseitige Energieaufnahme siehe 1.3. 7.2. Beziehung zwischen Stromstärke und Windungszahlen Materialien (zusätzlich): - Aufbau: Schaltbrett Widerstand R=100 Schiebewiderstand Durchführung: a) Widerstand konstant, Windungszahlen variieren indirekte Proportionalität: N1 I 2 N 2 I1 b) N1, N2 konstant, Widerstand variieren Schiebewiderstand Schiebewiderstand variieren Indirekte Proportionalität gilt nur für kleine Widerstände! Wissen: Sekundärstromstärke hier wegen Leistungsverlusten oft etwas geringer Zu 1c) und 2) Transformator ist ähnlich einer Stromquelle mit Innenwiderstand! Ist RΩ groß, also groß gegen RI des Transformators, so ist Uind = U0 (praktisch null Spannung fällt an UI ab) und das Transformatorgesetz für U gilt. Bei kleinem I jedoch wirken sich die ebenfalls kleinen Leistungsverluste im Transformator relativ stark aus. Trafogesetz für I gilt nicht! Ist RΩ klein, also klein gegen RI des Transformators, so ist Uind > U0 (praktisch komplette Spannung fällt an UI ab) und das Transformatorgesetz für U gilt nicht. Wegen PP = PS = U * I steigt jedoch die Stromstärke stark an. Bei großem I jedoch wirken sich die ebenfalls kleinen Leistungsverluste im Transformator nicht mehr aus. Trafogesetz für I gilt! U0 (Uind) = Uklemm + UΩ; d.h. beispielsweise eine Batterie wäre kaputt. Transformator kann durch Regulieren von U und I PP = PS aufrechterhalten!! 8. Licht und Schatten 1. Handbuch des Physikunterrichts (Sekundarbereich I/Band 4/1: Optik); Götz,Dahnke, Langensiepen; S. 69ff 2. Zwei Halogenlampen auf Dreierbank (Schrank 7.1) und eine Styroporkugel vor einen Schirm halten. Licht, Halb- und Kernschatten zeigen. 3. Globus bestrahlen: a) Tag und Nacht durch drehen zeigen (Schatten=Nacht; Licht=Tag) b) Jahreszeiten durch Lage der Erdachse erklären c) Mondphasen (Neu-, Voll-, zunehmender und abnehmender Mond) mit Styroporkugel und Globus zeigen d) Mond- und Sonnenfinsternis mit Styroporkugel und Globus zeigen 9. Eigenschaften von Spiegelbildern 9.1. Eigenschaften entdecken Bei allen Versuchen sollte der Spiegel auf Höhe der Tischplatte sein, deswegen den Spiegel über Stativstangen befestigen. a) Betrachte Gegenstände, z.B. Würfel, Playmobilfigur mit gehobener Hand im Spiegel b) Blatt mit einer eingezeichneten Straße vom Wirtshaus nach Hause Durchführung: - Ein Schüler soll mit einem Stift die eingezeichnete Straße vom Wirtshaus nach Hause nachfahren Ein anderer Schüler verdeckt dem “Fahrer” mit einem Blatt Papier die Sicht nach unten auf seine Hände c) Schreibe Deinen Namen in Druckbuchstaben auf ein Blatt Papier, wenn Du das Blatt und den Stift nur im Spiegel siehst. Der Spiegel muss nur im Spiegel lesbar sein. Erkenntnis aus a)-c): Spiegel vertauscht nur vorne und hinten, Rest bleibt gleich d) Schüttversuch Durchführung: Stelle einen Spiegel mit der Spiegelfläche senkrecht zu deinem Tisch. Befestige ihn mit dem Stativ. Nimm ein Glas und stell es vor den Spiegel, so dass du es gut siehst. Lass einen Mitschüler ein zweites Glas dorthin stellen, wo du das Spiegelbild des ersten Glases siehst und versuche nur in den Spiegel blickend mit dem dritten Glas Wasser in das Zweite zu gießen. Erkenntnis: Bild des Gegenstands liegt hinter Spiegel e) Kerze brennt Statt einem Spiegel verwendet man hier eine reflektierende Glasscheibe und 2 Teelichter. 1 Teelicht wird vor der Glassscheibe angezündet, das zweite Teelicht wird hinter die Scheibe gestellt. Der Schüler kann nun die Kerze vor dem Spiegel so verschieben, dass die Flamme dieser Kerze die zweite Kerze „entzündet“. Danach kann man den Abstand beider Kerzen vom Spiegel mit einem Maßband ausmessen. Erkenntnis: Entfernung Gegenstand-Spiegel = Entfernung Spiegel-Spiegelbild 9.2. Entdeckung des Reflexionsgesetzes 1. Versuch: Materialien: - 2 lange Pappröhren - 1 Taschenlampe - Spiegel - 2 Schüler Durchführung: - Röhren schräg an den auf den Tisch gelegten Spiegel halten, so dass sich ihre Enden nahe über dem Spiegel berühren - 1 Schüler leuchtet mit der Taschenlampe in eine der Röhren, der andere schaut durch die zweite Röhre und versucht das von Spiegel umgelenkte Lichtbündel zu finden - Lage der beiden Röhren zueinander bestimmen - möglichst an einer Wand durchführen, damit der Lichtweg z.B. mit Lineal nachvollzogen werden kann und die Winkel gemessen werden können Anhang: - Nach dem Reflexionsgesetz muss der Einfalls- gleich dem Ausfallswinkel sein - Man stellt fest, dass das menschliche Auge das Spiegelbild dort wahrnimmt, wo es gar keines gibt. Dieses Bild nennt man virtuelles Bild, weil keine wirklichen Strahlen von ihm ausgehen. - Man die reflektierten Strahlen nicht von solchen unterscheiden kann, die bei Abwesenheit des Spiegels von einer Punktquelle am Ort des Bildes ausgehen - Gegenstände werden auf die gleiche Größe ab. Es werden nicht oben und unten oder rechts und links, aber vorne und hinten vertauscht. Der Grund ist, dass die dem Betrachter abgewandte Seite des Gegenstands näher am Spiegel liegt und somit in dessen vorderer Bildebene abgebildet wird und umgekehrt. 2. Versuch: Aufgestellter Spiegel Stift unter bestimmtem Winkel an den Spiegel legen 2. Stift so anlegen, dass er Verlängerung des Spiegelbilds des 1. Stifts ist Kann auch mit einer Taschenlampe durchgeführt werden! 3. Versuch: Korkplatte mit Stecknadeln mit verschiedenen Nadelkopffarben - Korkplatten flach auf den Tisch vor Spiegel legen - mit einer Taschenlampe (eventuell Lichtstrahl abkleben um feineren Lichtstrahl zu erhalten) Licht auf Spiegel werfen und einfallenden und reflektierten Lichtstrahl mit Stecknadeln abstecken - verändere Einfallswinkel und führe den Versuch mit der zweiten Stecknadelfarbe nochmal durch jeweils gilt: Einfallswinkel = Ausfallswinkel 10. Modellversuche zu Auge und Fotoapparat 10.1. Modellgetreuer Aufbau des Auges Materialien: - Optische Bank (95cm) Kerze Linse: f=15cm Schirm Iris-Blende Aufbau: Strahlengang: a) weit entfernte Strahlen: b) nahe Strahlen: Demonstration der Kurz- und Weitsichtigkeit Materialien: - Aufbau: Optische Bank (95cm) Halogenlampe 12V Gelber Netzwürfel 12V Linse: f=15cm Schirm Iris-Blende Dieser Aufbau eignet sich wesentlich besser zur Demonstration der Kurz- und Weitsichtigkeit, auch wenn die Proportionen des Auges bei diesem Versuchsaufbau nicht mehr gegeben sind. Durchführung: a) Scharfes Bild der Glühwendel symbolisiert normal sehendes Auge b) Kurzsichtigkeit: Augapfel ist zu lang Schirm nach hinten verschieben - Korrektur mit Zerstreuungslinse (f= - 10) zwischen Licht und Blende - Brennebene der Augenlinse liegt vor der Netzhaut (siehe unten) c) Weitsichtigkeit: Augapfel ist zu kurz Schirm nach vorne - Korrektur mit Sammellinse (f= +10) - Brennebene der Augenlinse liegt hinter der Netzhaut Theorie: a) Kurzsichtigkeit b) Weitsichtigkeit Allgemein: Bei jeder Abbildung mit einer einfachen Sammellinse erscheint ein reelles Bild auf dem Schirm, d.h. es ist seitenverkehrt und auf dem Kopf (Punktspiegelung) 10.2. Fotoapparat Modellversuch Materialien und Aufbau: fast wie in 13.1., Linse und Blende tauschen hier jedoch Position. Linse Fotolinse Blende Blende für Tiefenschärfe Schirm Belichteter Film Durchführung: Um ein scharfes Bild der Wendel zu erhalten verschiebt man dieses mal die Filmlinse. Diese ist einziges bewegliches Teil des Fotoapparats. Wissen: Unterschied Auge – Fotoapparat: Auge: Linsenstärke variabel Foto: Linsenposition variabel 10.3. Demonstration des Einflusses der Blendenöffnung auf Schärfentiefe Je kleiner die Öffnung der Blende, desto schärfer das Bild, aber auch desto dunkler. Zur Demonstration der Tiefenschärfe schiebt man die Lampe nach vorn oder hinten. Derjenige Bereicht, der die Lampe noch einigermaßen scharf abbildet nennt man Tiefenschärfe. Einfluss der Blendenöffnung kann z.B. gezeigt werden über: das Bild ist am vorderen Rand der Schärfentiefe Blende weiter schließen Bild wird wieder schärfer Info zur Schärfentiefe: Für eine vorgegebene Gegenstandsweite g wird ein Gegenstand in einer bestimmten Bildweite scharf auf den Film abgebildet. Außerdem werden auch noch Gegenstände bis zu bestimmten Entfernungen davor und dahinter, d.h. mit g1 g und g 2 g , hinreichend scharf abgebildet. Den Bereich zwischen g1 und g 2 nennt man Schärfentiefe. Je kleiner die Blendenöffnung, desto größer ist dieser Bereich. 11. Optische Instrumente 11.1. Diaprojektor Materialien: - Optische Bank Lampe Gelber Netzwürfel 12V 1 Sammellinse (f = +5) 2 Kondensorlinsen (die sind ein bisschen größer als die normalen Linsen) 1 Dia mit Halterung Schirm Aufbau: Kondensorlinsen in eine Halterung und zwar NAH an die Lichtquelle! (Strahlenverlauf falsch) Theorie: - Kondensorlinsen: sorgen für parallele Lichtstrahlen, die auf das Dia fallen. Paralleles Licht Licht weitet sich kaum aus - je kleiner die Brennweite der Linse, desto größer das Bild - Overheadprojektor nutzt gleiches Prinzip Warum ist Strahlengang falsch? Dia richtig oder verkehrt herum???????????????? 11.2. Mikroskop Materialien: - Aufbau: Optische Bank 2 Sammellinsen (f = 15, f= 5) Dia (eventuell Taschenlampe bei schlechten Lichtverhältnissen) Konstruktion: - Nah am Gegenstand: Objektiv (kleinere Brennweite): liefert vergrößertes reelles Bild - Nah am Auge: Okular: liefert nochmals vergrößertes virtuelles Bild - Dia fest in der Brennweite des ebenfalls festen Objektivs - Mit Auge nah an Okular gehen und so lange verschieben, bis scharfes Bild entsteht Theorie: - Je größer die Brennweite des Okulars, desto kleiner die Vergrößerung. - Objektiv liefert vergrößertes reelles Bild des Gegenstands, das mit dem Okular als Lupe nochmals vergrößert betrachtet wird - Strahlverlauf: 11.3. Galilei’isches Fernrohr Materialien: - Aufbau: Optische Bank 1 Zerstreuungslinse (f = - 10) 1 Sammellinse (f = 50) Konstruktion: - Zerstreuungslinse am Auge - Addition aus Brennweiten der beiden Linsen ergibt ca. den Abstand Theorie: Objektiv ist Sammellinse die Gegenstand abbildet, aber hier wird kein Zwischenbild erzeugt: Sammellinse des Objektivs bricht das nahezu parallel einfallende Lichtbündel vom weit entfernten Gegenstand. Bevor es sich aber im Brennpunkt des Objektivs vereinigen kann wird es durch die Zerstreuungslinse aufgeweitet, so dass es hinter der Linse als Parallellichtbündel weiterläuft. Die Zerstreuungslinse ist so gewählt, dass sie die Wirkung der Augenlinse weitgehend aufhebt, deshalb erzeugt das Objektiv das Bild direkt auf der Netzhaut. Da es eine größere Brennweite hat als die Augenlinse, sind der Sehwinkel und das Bild größer. Vergrößerungsformel: V fObjektiv fOkular 11.4. Kepler’sches Fernrohr Materialien: - Optische Bank 2 Sammellinsen (f = 15, f = 30) Aufbau: Umkehrung der Linsenanordnung vom Mikroskop Hier entsteht Zwischenbild, das mit Okular betrachtet wird! Konstruktion: - Sammellinse mit kleinerer Brennweite am Auge - Addition aus Brennweiten ergibt auch hier den Abstand der Linsen. - Strahlverlauf: Achtung: Hier steht Bild im Gegensatz zum Galilei-Fernrohr auf dem Kopf, weil das eigentlich richtig aufrecht auf der Netzhaut! Theorie: Das Objektiv erzeugt in seiner Brennebene auf dem Kopf stehende Bilder von weit entfernten Gegenständen. Diese Zwischenbilder werden mit dem Okular als Lupe vom Auge betrachtet. Objektiv und Okular tragen zur Vergrößerung bei. Die Anordnung liefert eigentlich ein aufrechtes und seitenrichtiges Netzhautbild, wird aber vom Gehirn in ein seitenverkehrtes und kopfstehendes Bild umgewandelt. 12. Abbildung durch Linsen 12.1. Abbildungsformel qualitativ präsentieren Materialien: - Optische Bank Kerze 1 Sammellinse (f = 10) Schirm Aufbau: Durchführung: Kerze fest auf Schiene justieren bestimmte Gegenstandsweite g (Entfernung Kerze – Sammellinse) einstellen und Schirm so lange verschieben, bis scharfes Bild der Flamme (= Bildweite b) erscheint Dies wird durchgeführt mit g<f, g=f, f<g<2f, g=2f, g>2f Ergebnis: Aus Strahlensatz-Überlegungen folge zudem: B b G g 12.2. Möglichkeiten zur Bestimmung der Brennweite einer Sammellinse a) Verwende 1 1 1 um die Brennweite f zu bestimmen, d.h. verwende 16.1. und messe die f g b Gegenstandsweite g und Bildweite b. b) Schätze die Brennweite über virtuelles Bild ab, d.h. nähere Dich mit der Linse dem Gegenstand an, bis man ein erstes scharfes Bild erhält c) Verwende Lupenfunktion (g<f): „Blatt“ ankokeln 12.3. Optische Wandtafel Materialien: - Wandtafeloptik (22.4) Linse mit möglichst großer Krümmung Farbfilter Gelbes Netzgerät Aufbau: Durchführung: Sphärische Aberration: Leuchtkörper Brennpunkt Randstrahlen Brennpunkt der näher am Mittelpunkt liegenden Strahlen Man sieht: Die parallelen Lichtstrahlen werden am Rand stärker gebrochen als die in der Mitte Erklärung: Geometrie der Linse: Der Effekt, dass achsenferne Strahlen zu stark gebrochen werden, tritt dann auf, wenn Linsen mit kugelförmigen Linsenoberflächen, d.h. mit konstantem Radius zum Linsenmittelpunkt hin, verwendet werden (sphärische Linsen). Chromatische Aberration: Durchführung: Zunächst wird vor die Lampe ein roter Filter gebracht und der Strahlengang wird nachgezeichnet. Anschließend wird ein blauer Filter angebracht und der Strahlengang ebenfalls nachgezeichnet. Die unterschiedlichen Brennpunkte kann man anschließend direkt am Papier sehen. (a) Roter Filter: (b) Blauer Filter: Erklärung: Die Brechung ist von der Wellenlänge des einfallenden Lichts abhängig. Kleinere Wellenlängen werden stärker gebrochen. Deshalb wird blaues Licht stärker gebrochen als rotes Licht. Somit ist der Brennpunkt des roten Lichts gegenüber des blauen Lichts weiter von der Linse entfernt. 13. Zerlegung von weißem Licht in Spektralfarben 13.1 Zerlegung von weißem Licht mit Prisma Materialien: - Aufbau: Optische Bank Gelber Netzwürfel (12 V) oder blaues Netzgerät (10 V) Lampe 2 Linsen mit f=5cm und f=10cm Regelbarer Spalt (senkrecht aufgestellt) Weißer Schirm Prisma mit Halterung und Reiter (evtl. besser mit 9cm, 21cm, 13cm, 14cm durchführen) Durchführung: Versuch zuerst ohne Prisma aufbauen, so dass Spalt scharf auf dem weißen Schirm abgebildet wird. Prisma in den Strahlengang stellen Farbaufspaltung auf nun schräg gestelltem Schirm sichtbar (nicht mehr auf optischer Achse) Sonstiges: Linse 1 soll für paralleles Licht sorgen (leuchtet den Spalt schön aus), Brennpunkt nicht so wichtig, ruhig näher als Brennweite an Lampe stellen Spalt schön ausleuchten, nicht überstrahlen, zuständig für schmales Lichtbündel Keine Schatten und sonstige störende Figuren auf Schirm Durch Drehen des Prismas kann die Darstellung des Spektrums verändert werden (breiter oder schmäler) Brechung: n 1 Dispersion: unterschiedlich starke Brechung von verschieden farbigem Licht (blaues Licht wird stärker gebrochen als rotes Licht) 13.2 Vereinigung des Spektrums zu weißem Licht Materialien: Zusätzlich: Sammellinse mit f=5cm (oder f=10cm) Aufbau: Durchführung: Sammellinse zwischen Prisma und schräg gestelltem Schirm mit Abstand zwischen Prisma und Linse = fLinse halten Paralleles Licht Vereinigung der Spektralfarben zu weißem Licht Wissen: Es gibt zwei Arten von Farbmischung: Additive Farbmischung: Übereinanderstrahlen verschiedener Lichtfarben. (d.h. nur bei Licht möglich) Subtraktive Farbmischung: Das Erzeugen von Farben mittels Ausblenden durch Farbfilter. Ein Filter lässt nur dasjenige Licht durch, das der Wellenlänge (also der Farbe) des Filters entspricht. 13.3 Zusatzfragen Auswirkung der Breite des Lichtbündels auf das Spektrum: Breite des Lichtbündels durch Variation der Spaltbreite erreichbar. Je schmäler das Lichtbündel (d.h. je schmäler der Spalt), desto dunkler und schärfer das Spektrum. Auswirkung verschiedener Filter auf das Spektrum: Das Ausblenden von Farben geschieht mit Farbfiltern subtraktive Farbmischung Beispiel: Ein gelbes Farbfilter lässt nur die Farbe Gelb passieren und meist auch die dicht benachbarten Farben Rot und Grün. Blau und Violett wird vollständig absorbiert. Der komplementäre Anteil, der mit Gelb zusammen die Farbe Weiß ergeben würde, wird absorbiert. Durchführung: - einzelne Filter: nur noch entsprechende Farbe des Filters am Beobachtungsschirm, alle anderen Farbanteile des weißen Lichts werden absorbiert. Kombination zweier oder mehrerer Filter: Mischfarbe der Filter am Schirm. Bei gleichzeitiger Verwendung von Filtern der drei Grundfarben Gelb, Blau/Cyan und Rot/Magenta passiert kein Licht die Filter Auswirkung der Verringerung der Versorgungsspannung: Durch Verringerung der Versorgungsspannung verändert man das Licht der Lampe, das bei einer Spannung von etwa 10 V weiß ist, bei niedrigeren Spannungen eher gelblich ist Veränderung der Wellenlängen der Lampe zu größeren Wellenlängen bei der Lampe Im Spektrum verschwindet der Violettanteil, weil die Spannung nicht mehr ausreicht, um die kurzen Wellenlängen anzuregen. Das Spektrum wird insgesamt dunkler, die Mitte des Spektrums (gelb) am intensivsten, etwas schmäler. Gesetz, das hier veranschaulicht wird: Vermutung: Intensitätsverteilung hängt von der Wellenlänge ab. Komplementärfarben: Am besten am Farbkreis erkennbar: - gegenüberliegende Farben sind komplementär - additive Mischung der Grundfarben rot, grün, blau ergibt jeweils die eingeschlossene Farbe - subtraktive Mischung der Grundfarben gelb, cyan, magenta ergibt jeweils die eingeschlossene Farbe 14. Qualitative Versuche zur Ausdehnung von Festkörpern, Flüssigkeiten und Gasen bei Erwärmung 14.1. Freihandversuche a) Festkörper Materialien: - Metallkugel mit passendem Loch (10.4) - Bunsenbrenner - Zange Vor dem Erhitzen passt die Kugel durch das Loch. Nach dem Erhitzen funktioniert dies nicht mehr. Zusatz: Erhitzt man nachträglich noch das Loch der Halterung passt die Kugel auf einmal wieder durch das Loch! Grund Äußerer Streifen wird mehr ausgedehnt wie kleinerer innerer (der beim Loch), da Ausdehnung proportional zu l 0 ist. Aufgrund der Oberflächenspannung ziehen die äußeren „Streifen“ die inneren nach außen Loch wird größer b) Flüssigkeiten Thermometer in der Hand halten, Flüssigkeitspegel (z.B. Quecksilber) steigt c) Gase Luftballon auf Flasche mit sehr wenig Wasser darin schnallen. Flasche in warmes Wasser stellen Ballon füllt sich mit Luft 14.2. Materialabhängigkeit der Ausdehnung bei Flüssigkeiten Materialien: - 2 Erlenmeyerkolben (100ml) - 2 Stopsel mit Glaskapillaren (9.4) - Glaswanne mit heißem Wasser (4.4) - Flüssigkeiten (Wasser, Spiritus, Frostschutzmittel…) (draußen auf Regal) Aufbau: Durchführung: - Erlenmeyerkolben mit Flüssigkeiten befüllen und den Stopsel so tief eindrücken bis die Flüssigkeitssäulen die Markierung erreichen. - beide Kolben in das heiße Wasserbad stellen Ergebnis: Wärmeausdehnung ist stoffabhängig, da die Flüssigkeitssäule mit Spiritus viel schneller ansteigt als die mit Wasser. Erklärung: Wasser hat größere Wärmekapazität! Zwischen Spiritus und Frostschutzmittel kein so großer Unterschied, da beide ganz bzw. teilweise aus Alkohol bestehen. 14.3. MaterialUNabhängigkeit der Ausdehnung bei Gasen Materialien: - 2 Erlmeyerkolben - 2 Kolben mit Stopsel - Gas, z.B. Kohlendioxid, Helium, Luft - Wasserbad mit heißem Wasser Durchführung: Genau wie in 18.2. Ergebnis: Beide Kolben steigen ungefähr gleich stark an, d.h. die Gase in den Kolben dehnen sich ungefähr gleich stark aus Ausdehnung von Gasen ist materialunabhängig Erklärung: Im Gegensatz zu Festkörpern und Flüssigkeiten haben Gase keine Molekülbindungen. Nur diese dehnen sich bei unterschiedlicher DichteDer Druck den die Gase verursachen ist bei allen gleich, obwohl sich Gase, die leichter als Luft sind, schneller ausdehnen, als diejenigen, die schwerer sind. 14.4. Technische Anwendung von Erwärmung von Festkörpern Materialien: - Bimetallstreifen (16.2): Streifen aus 2 unterschiedlichen Metallen - Blauer Netzwürfel (Wechselspannung, 12V) - Klingel - Krokodilklemmen - Kabel Aufbau: Durchführung: - Bimetallstreifen sollte zu Beginn auf Kontakt aufliegen. - Spannung aufdrehen auf ca. 12V Klingel läutet, hört auf und fängt wieder an Erklärung: Bei zu starker Erhitzung des Bimetallstreifens wird der Kontakt unterbrochen, da sich die beiden Materialien des Bimetallstreifens unterschiedlich stark ausdehnen. Kühlt der Streifen wieder ab wird der Kontakt wieder hergestellt, es klingelt, usw. Anwendung: Temperaturregler in Bügeleisen, Elektroherd 15. Quantitative Untersuchung der Ausdehnung von Festkörpern bei Erwärmung 15.1. Längenausdehnung quantitativ Materialien: - Messingrohr mit Skala (10.4) - Wasserdampfkesselchen (10.4) - Wassergefäß zum Auffangen des Wassers nach dem Rohr - Thermometer bzw. Oberflächenfühler (14.3) Aufbau: Durchführung: - Temperatur des Messingsrohrs mit Festkörperthermometer bestimmen, Länge l des Rohrs messen, Anzeige auf 0 eichen - Wasserdampfkessel einschalten Längenänderung kann von Anzeige abgelesen werden, Temperaturänderung kann über Taktuell TAnfang berechnet werden l T 65⁰C ≈ o,85mm 49⁰C ≈ o,6mm 24⁰C ≈ o,3mm 15.2. Längenausdehnung proportional zur Anfangslänge Materialien und Aufbau: genau wie bei 15.1. Durchführung: - verschiebe Verstellschraube (die Schraube fixiert den Stab auf einer Seite festes Ende der Stab weitet sich nur in die Richtung der Anzeige aus) um Anfangslänge zu variieren - Lese l an Anzeige ab - Führe diesen Versuch mit den 3 möglichen einstellbaren Anfangslängen durch Ergebnis: Auswertung z.B. mit einem l0 l - Diagramm Gerade l0 l Die Ausdehnung l ist also umso größer, je größer die Anfangslänge des Stabs ist. 15.3. Gesetzmäßigkeit l T l l0 l T l0 l k l0 T k l l0 T Längenausdehnungskoeffizient: l l0 T 15.4. Längenausdehnungskoeffizient von Messing Bestimme den Längenausdehnungskoeffizient von Messing über: l 0,8mm 1 (Literatur: 16 106 l T 600mm 80 K K 1 18,5 106 ) K 15.5. Volumenausdehnungskoeffizient von Wasser Materialien: - Alubecher (10.5) - Erlenmeyerkolben 250ml - Gummistopfen mit 2 Löchern (9.4) - 1. Loch: Kapillar mit Markierung - 2. Loch: Thermometer Lineal mit Markierecken Stativstangen Wasser Schiebelehre zum Vermessen des Radius des Kapillars Aufbau: Durchführung: a) Bestimme V0 des Wassers im Erlenmeyerkolben, z.B. in Messbecher schütten b) Steighöhe des Wassers bei verschiedenen Temperaturen markieren c) V über V = r 2 h berechnen Ergebnis: Versuch reicht eigentlich nicht aus, um die Formel V herzuleiten, da nur V T V0 T bewiesen wurde. Es müsste also in einem zweiten Versuchsteil die Abhängigkeit der Volumenänderung vom Ausgangsvolumen untersucht werden (z.B. mit unterschiedlich großen Kolben). Hier wird also die die Formel als gegeben vorausgesetzt. Messung lieferte für die Volumenausdehnung der Wasser: 0, 21 10 3 V V0 T (Literaturwert: 1 ) K Anwendung im Alltag zur Motivation der Schüler: Wie überleben eigentlich die Fische im Winter? Anomalie des Wasser: Das Volumen von Wasser ist bei 4°C am kleinsten, somit ist die Dichte dort am größten im Winter liegt Wasser mit 4°C also tiefer als das Eis mit 0°C 16. Trägheitssatz und Wechselwirkungsgesetz 23.1a) Didaktische/methodische Funktion, Ziele des Versuchs: Mit einfachen Mitteln soll den Schülern der Begriff "Trägheit" gezeigt und genauer betrachtet werden Materialien: - Stativ mit Arm - Holzklotz mit je einem Hacken an Ober- und Unterseite - eine Rolle Nähfaden Aufbau: An beiden Hacken des Holzklotzes wird ein Nähfaden befestigt. Einer der Fäden wird an dem Arm des Stativs befestigt. Durchführung: Man zieht zuerst langsam am unteren Ende des unteren Faden, so lange bis einer der beiden Fäden reißt. Darauf baut man den Versuch anfangsgemäß wieder auf und nun zieht man schnell am unteren Fadenende. Tipps und Tricks: Man sollte einige Bindfäden schon mit Schlaufen versehen, damit man die Bindfäden schnell ersetzten werden können und nicht zu viel Zeit im Unterricht verloren geht. Der erste Teil des Versuches muß evtl. öfters durchgeführt werden da es schwer zu erkennen ist wo er zuerst reißt. Beobachtung: Langsames Ziehen: Der Faden zwischen Stativarm und Holzklotz sollte reißen. Schnelles Ziehen: Der untere Faden sollte reisen. Erklärung: Langsames Ziehen: Hierbei wirkt auf den unteren Faden nur die ausgeübte Zugkraft. Im Gegensatz dazu wirkt auf den Oberen die Zugkraft und die Gewichtskraft des Holzklotzes. Da die angreifende Kraft am Oberen größer ist, reißt dieser Faden. Schnelles Ziehen: Durch das schnelle anreißen am unteren Faden wirkt die Zugkraft zuerst auf ihn ein. Der Körper wirkt nun eine Kraft entgegen zur Zugrichtung aus. So wirkt auf den oberen Faden die Zugkraft minus der Gegenkraft des Holzklotzes. Auf den Unteren, die Zugkraft. Somit reißt beim schnellen ziehen der untere Faden. b) Didaktische/methodische Funktion, Ziele des Versuchs: Mit diesem Versuch soll gezeigt werden, dass Gegenstände unterschiedlicher Masse gleich schnell zu Boden fallen. Materialien: - Kamera (mit Slow-motion-Funktion) oder Blech 2 Stühle Blatt Papier oder Postkarte 3 gleiche Münzen Tesa Aufbau: - Klebe zwei der drei Münzen zu einer mit Tesa zusammen Rücke die zwei Stühle mit den Lehnen zusammen (halte zwischen den Stühlen ca. 5 cm Abstand) Lege das Papier/Postkarte über die Lehnen und die beiden Münzen (zusammengeklebte + einzelne) darauf Richte die Kamera auf den Zwischenraum der Stühle Skizze: Durchführung: Die Kamera einschalten und auf Aufnahme drücken. Anschließend das Papier/Postkarte ruckartig wegziehen, sodass die beiden Münzen, ohne einen der Stühle zu berühren, auf den Boden fallen. Alternative: Man kann anstelle der Kamera auch ein Blech benutzen, indem man die Münzen (wie oben beschrieben) aus verschiedenen Höhen, auf das Blech fallen lässt. Skizze: Tipps und Tricks: Beachte bei der Versuchsdurchführung mit der Kamera auf folgendes: - - Hintergrund sollte sich farblich von den Münzen absetzen (z.B. Tafel) Kamera sollte in halber Fallhöhe und gerade gerichtet auf den Versuchsaufbau stehen (oberer Bildrand: Münzen auf Papier, unterer Bildrand: Boden, Aufschlagspunkt der Münzen) Zwischen Aktivieren der Kamera und Wegziehen der Papierunterlage genügend Zeit lassen, damit man anschließend bei der Zeitlupenbetrachtung den Fallvorgang leichter beobachten werden kann Zur besseren Auswertung sollte die Kamera an einen Fernseher angeschlossen werden Münzen dürfen beim Fall die Stuhllehnen nicht berühren Beobachtung: Bei der Betrachtung der Zeitlupe fällt auf, dass beide Münzen sich stets auf gleicher Höhe befinden, obwohl sie unterschiedliche Masse haben. Bei der alternativen Durchführung hört man, dass die Münzen jeweils gleichzeitig aufschlagen. Erklärung: Auf der Erde wirkt die Schwerkraft, sonst würden alle Dinge auf der Erde davonschweben. Wichtig dabei ist, dass die Schwerkraft auf alle Dinge gleich wirkt, z.B. ein Papierknäuel und eine Eisenkugel fallen gleichschnell. Hintergrundinformation: Beim freien Fall (ohne Luftwiderstand) ist die beschleunigende Kraft die Schwerkraft M*g (M: schwere Masse). Mit Newton II folgt also: M*g = m*a (m: träge Masse). Nur weil schwere und träge Masse gleich sind, ergibt sich: a = g. D.h. beim freien Fall werden alle Körper am gleichen Ort (g ortsabhängig) gleich schnell beschleunigt. In der Praxis fallen Gegenstände nicht gleichschnell (vgl. Feder/Eisenkugel), da Reibungskräfte wirken. 16.2. 16.3. 17. Addition von Kräften 17.1. Blattfeder mit Schraubenzwinge an Tisch befestigen und mit Kraftmesser in verschiedenen Richtungen nach unten ziehen. Vergleiche Angriffswinkel und Wirkung der verschiedenen Kräfte. 17.2.Materialien: - Magnettafel 2 Magnettafel-Newtonmeter (im kleinen Seminarraum) Gewicht 200g Aufbau: Durchführung: - - Ausrichten der Magnettafeln (0 der Skala nach oben), Faden beider Tafeln einmal um die Rolle wickeln Gewicht an beide Fäden hängen Für schöne Werte die Position beider Kraftmesser verändern Mit Lineal und bunter Kreide Kraftpfeile einzeichnen: Richtung ergibt sich aus Verlängerung der jeweiligen Schnur, Betrag wird von der Skala abgelesen und mit geeigneten Maßstab (z.B. 10 cm = 1N) eingezeichnet Resultierende Kraft durch Parallelverschiebung der beiden Kraftpfeile einzeichnen Abmessen des Betrags des resultierenden Kraftvektors Ergebnis: Kräfte addieren sich vektoriell Sonstiges: Weitere Möglichkeit Kräftezerlegung zu demonstrieren: schiefe Ebene Würde man die Kräfte nach unten anzeichnen, so zeigt man nur die Aufteilung der Gewichtskraft. Dies ist aber in der Fragestellung nicht verlangt. 18.Auftrieb in Flüssigkeiten und Gasen Gesetz von Archimedes: Ein in eine Flüssigkeit eintauchender Körper verliert so viel von seiner Gewichtskraft, wie die von ihm verdrängte Flüssigkeitsmenge wiegt. Der Gewichtsverlust des Körpers entspricht dem sog. Auftrieb, den der Körper in der Flüssigkeit erfährt. Ursache ist der Schweredruck. Je tiefer ein Körper eintaucht, desto größer wird die Auftriebskraft. Ist er vollständig eingetaucht, so verändert sich die Auftriebskraft nicht mehr. 18.1. Qualitative Versuche zur Auftriebskraft a) Flüssigkeit: Materialien: Glas Wasser, Gewicht, Newtonmeter Aufbau: Ergebnis: Gewicht ist laut Newtonmeter im Wasser leichter b) Gase: Materialien: - Vakuumpumpe (Schrank 28 im Gang) - Gewichtsbaum mit Gewicht und leicht schwererer Styroporkugel (1.4.) Aufbau: Durchführung: In der Luft halten sich beide Gegenstände im Gleichgewicht, obwohl sie unterschiedlich schwer sind. Grund: unterschiedliches Volumen sorgt für verschieden starke Auftriebe in Luft Saugt man die Luft mittels der Pumpe aus der Glocke sinkt die Styroporkugel und beide Gegenstände sind nicht mehr im Gleichgewicht. Grund: im Vakuum gibt es keine Auftriebskraft die schwerere Kugel sinkt 18.2. Experimente zur induktiven Gewinnung des Gesetzes von Archimedes Abhängigkeiten der Auftriebskraft a) von der Körperform Materialien: - Knetmasse (oder alternativ: zwei Aluminiumkörper gleicher Masse aber unterschiedlicher Körperform) - Schnur - Kraftmesser - Wassergefäß mit Wasser (4.2.) Aufbau: Durchführung: Knetmasse einmal als Kugel, einmal als flachen Datschi an Kraftmesser hängen gleiche Masse, gleiche Dichte, also gleiches Volumen, aber unterschiedliche Körperform Ergebnis: Die Auftriebskraft ist unabhängig von der Körperform. Der Kraftmesser zeigt bei beiden Körperformen die gleiche Kraft an auf beide Körperformen wirkt die gleiche Auftriebskraft. b) von der Eintauchtiefe Materialien: - großer Glaszylinder - Gewicht Schnur ca. 10cm Kraftmesser Aufbau: Durchführung: Der Körper muss sich immer vollständig unter Wasser befinden: 1) Gewichtskraft des Körpers in Luft bestimmen 2) Gewichtskraft knapp unterhalb der Wasseroberfläche bestimmen 3) Gewichtskraft knapp über dem Gefäßboden bestimmen Ergebnis: Auftriebskraft ist unabhängig von der Eintauchtiefe c) von der Dichte der Flüssigkeit Materialien: - Gefäß mit Wasser - Gefäß mit Salzwasser (hoher Salzgehalt) - Gewicht 100g (nicht zu schwer) - Kraftmesser Aufbau: Durchführung: Gewichtskraft des Körpers im Wasser und anschließend im Salzwasser messen. Kraftmesser zeigt im Salzwasser geringeren Ausschlag an! Ergebnis: Auftriebskraft ist ABHÄNGIG von der Dichte der Flüssigkeit F ρFlüssigkeit Bemerkung: Fast kein Effekt sichtbar! d) von der Körpermasse Materialien: - 2 Metallquader, z.B. Eisen und Aluminium mit gleichem Volumen aber deutlich unterschiedlicher Masse - Kraftmesser - Becher und Wasser Aufbau: Durchführung: Für beide Metallquader jeweils in Luft und vollständig unter Wasser die Gewichtskraft bestimmen: In Luft: In Wasser: FFe=0,45 N; FAl=0,15 N FFe=0,40 N; FAl=0,1N FAuftrieb=FLuft-FWasser=0,05N bei beiden Elementen Ergebnis: Auftriebskraft ist unabhängig von der Körpermasse e) vom Körpervolumen Materialien: - 2 Zylinder mit je 200g und unterschiedlichem Volumen - Kraftmesser - Becher und Wasser Aufbau: unterschiedlicher Ausschlag Ergebnis: Auftriebskraft ist ABHÄNGIG vom Volumen des Körpers F VKörper Gewinnung des Gesetzes von Archimedes: F ρFlüssigkeit und F VKörper somit ist FAuftrieb VK F FAuftrieb = k VK F . Die Konstante ist in diesem Fall der Ortsfaktor g, was zur Formel führt: FAuftrieb = g VK F 18.3. Bestätigung des Gesetzes von Archimedes quantitativ Materialien: - Überlaufgefäß - Kraftmesser - Messzylinder - Faden mit Schlaufen - Körper, z.B. 100g-Massestück - Stativmaterial Aufbau: Durchführung: Überlaufgefäß so lange mit Wasser füllen, bis dieses auszufließen beginnt. Messzylinder unter das Überlaufrohr stellen. Wegen FAuf FLuft FWasser : - Gewichtskraft des Körpers in Luft messen Körper, der mit Faden am Federkraftmesser befestigt ist, in das Überlaufgefäß halten und Gewichtskraft im Wasser messen. Volumen des verdrängten Wassers am Messzylinder ablesen V = … ( 1Liter = 1dm3 ) Auswertung: Die auf den Körper wirkende Auftriebskraft wird durch Differenzbildung aus der Gewichtskraft in Luft und der Gewichtskraft in Wasser ermittelt: FAuf FLuft FWasser Umstellen der Archimedischen Formel liefert VK = FAuf g ρF Vergleich des rechnerischen Volumens mit dem gemessenen Volumens des übergelaufenen Wassers. Alternative: Das archimedische Prinzip liefert auch die Erkenntnis: Auftriebskraft ist gleich der Gewichtskraft der verdrängten Flüssigkeit, deswegen kann der Versuch auch so durchgeführt werden, dass man das Gesetz nicht nach VK auflöst und Werte einsetzt, sondern die Gewichtskraft der verdrängten Flüssigkeit bestimmt: - FAuftrieb = g VK ρF - Fg m g , wobei m Masse der verdrängten Flüssigkeit ist (Achtung: NUR Wassermasse wiegen) 18.4. Gesetz von Archimedes mit Balkenwaage und Überlaufgefäß Materialien: - Balkenwaage Gewichte Stativ mit Aufhängung Überlaufgefäß 2 Gefäße (nichtschwimmender) Körper Schnur kleine „Hebevorrichtung“ Aufbau: Durchführung: 1. Auf der rechten Seite der Waage stehen das Stativ mit dem in der Luft hängenden Gewicht und ein leeres Auffanggefäß. 2. Die linke Seite der Waage wird mit Gewichten beschwert, so dass sich die Waage im Gleichgewicht befindet. 3. Anschließend wird die Hebebühne erhöht, so dass das Gewicht ins Wasser vollständig eintaucht. Das überfließende Wasser läuft in ein zweites, neben dem Aufbau stehendes Auffanggefäß, das das überfließende Wasser auffängt die rechte Seite der Waage steigt 4. Nun füllt man das übergelaufene Wasser in das Gefäß auf der rechten Seite der Waage die Waage befindet sich wieder im Gleichgewicht Auftriebskraft ist gleich der verdrängten Gewichtskraft 19.20. Messwerterfassung mit dem Computer 1 und 2 - System Cassy erklären können - Kurzes Blockschaltbild: Sensor – Kabel – Box (jeden Sensor an eigene Schnittstelle) – Basismodul (= Schnittstelle zum PC; analog-digital-, digital-analog-, digital-digital-Wandler) – USB-Schnittstelle – Computer - - - Unterschied analog-digital: Analog: Messwert ändert sich ständig auf der Zeitachse, z.B. Sinussignal Digital: Messwert über bestimmtes Zeitintervall konstant, z.B. Rechtecksignal, helldunkel, high-low,1-0 Bei Boxen: jeweils oberen Anschluss verwenden In Software: Anschlüsse rot aktiv, wobei Aktivierung mit rechter Maustaste Messung starten mit Stoppuhr-Button Skalierung der Achsen ändern: mit rechter Maustaste z.B. unter Achse klicken 4 Versuche, vorhandene gespeicherte Dateien mit eingestellten Parametern verwenden (Messung laden): 28.1 Zeit-Weg-Messung Materialien: - Luftkissenfahrbahn (im großen Seminarraum) - Cassy - BMW-Box in Basismodul Input A Aufbau: - BMW-Box in Basismudul Input A - Relais einbauen (Kabelverbindung an Basismodul), um Magnet (für Start des Reiters) zu steuern Durchführung: - Datei z-Luftkissen_Daten laden - Reiter wird von Magnet gehalten und erst automatisch (per Computer gesteuert) losgelassen (Magnet abgeschaltet), wenn die Messung startet - Schnur sauber über Speichenrad laufen lassen - Rechtsklick auf s_A1-Fenster: Fenster mit zwei wichtigen Buttons: S -S : Vorzeichenumkehrung der Wegstrecke; vor 1. Messung durch manuelles Verschieben des Reiters kontrollieren, ob bei Streckenmessung gewünschtes Vorzeichen erfasst wird 0 : Button nach jeder Messung betätigen; setzt aufgenommene Wegstrecke auf Null - Bei neuer Messung: Gewicht dranhängen, Seilführung prüfen, Wegstrecke auf Null setzen Wissen: - Luftkissenschiene: Sensor am Ende, Speichenrad (Programm kennt Umfang des Rads, Anzahl der Speichen etc.), Reiter bewegt sich aufgrund des Gewichts, Infrarotsender, Infrarotempfänger Rechteckimpuls (kann nur zeitlich umgesetzt werden) - Digitale Messung, da hell-dunkel - 3 Parameter s, v, a - 3 Graphen darstellen; erklären, warum v linear, a konstant etc. - Formeln (Bewegungsgleichungen) im Kopf haben - Strecke der Fahrbahn beträgt 2,4 m schauen, wie viele Meter von Cassy gemessen werden können/sollen; bei beschleunigter Bewegung kommt Sensor irgendwann nicht mehr mit; Technik stößt an seine Grenzen; es kann passieren, dass irgendwann Werte addiert angezeigt werden 28.2 Schnelle Zeit-Weg-Messung Materialien: - Lichtschranke mit Stromversorgung 5 V - Fallkamm bestimmter Länge und mit bestimmter Anzahl von Durchlässen (hier: 21 Schlitze) - Pappschachtel zum Auffangen des Fallkamms - Stativmaterial für Lichtschranke - Cassy - Timer-Box in Basismodul Input A Aufbau: - Lichtschranke waagrecht mit Stativmaterial aufbauen - Timer-Box in Basismudul Input A - Stecker der Lichtschranke in Timer-Box (oben) Durchführung: - Datei g-Leiter laden - Bei Lichtschranke vor jedem Versuch Reset-Taste betätigen - Intensität der Lichtschranke so einstellen, dass das rote Lämpchen nicht leuchtet - Fallkamm durch Lichtschranke fallen lassen, wobei darauf geachtet werden muss, dass alle Schlitze von Lichtschranke erfasst werden - Versuch erfolgreich, wenn Zahl „21“ (steht für die 21 Schlitze des Kamms) auf Lichtschranke angezeigt wird, ansonsten Versuch nochmals machen Wissen: - Mit diesem Versuch kann die Erdbeschleunigung g bestimmt werden - Programm kennt die Länge des Fallkamms und die Anzahl seiner Durchlässe (hier: 21 Schlitze) - Digitale Messung, da Lichtschranke als Sensor auf Dunkel / Unterbrechung reagiert - Steigender Haken am Ende des Zeit-Beschleunigungs-Diagramms: Technik kommt wegen beschleunigter Bewegung nicht mehr mit, Geschwindigkeit zu schnell für Sensor 28.3 Fallröhre (Spulenstab von Neva) Materialien: - Fallröhre mit 6 Spulen in gleichen Abständen (sog. Spulenstab von Neva) - Cassy Spule - Keine Box Aufbau: - Spannung Input B mit Fallröhre verkabeln - Timer-Box in Basismudul Input A - Stecker der Lichtschranke in Timer-Box (oben) Durchführung: - Datei e-Fallröhre laden - Eisenfallkörper durch Fallröhre fallen lassen - Messung: nahezu gleichzeitig Messung starten und Körper durch Röhre fallen lassen Wissen: - Achtung Falle: Dieser Versuch ist NICHT zur Bestimmung der Erdbeschleunigung g geeignet! in diesem Versuch ist g-Faktor total daneben Lenzsche Regel; Wirbelströme bremsen Fallkörper beim Reinfallen, beschleunigen ihn beim Austritt aus der Spule - Untersucht wird in diesem Versuch die Abhängigkeit der Induktionsspannung von der Zeit - Analoge Messung (Spannungspeaks haben Ähnlichkeit mit Sinuskurve) - Strom sorgt für ein Magnetfeld in der Röhre - Im Fallkörper wird eine Spannung induziert, die nach der Lenzschen Regel der Ursache entgegenwirkt - Je größer die Änderung des Magnetfelds, desto größer die induzierte Spannung - Auswertung des aufgenommenen Zeit-Spannungs-Diagramms: Spannungspeaks werden mit der Zeit größer: beschleunigte Bewegung Körper dringt mit immer größerer Geschwindigkeit in Magnetfeld ein größere induzierte Spannung Peaks rücken näher zusammen, da die Geschwindigkeit des Fallkörpers zwischen den Spulen größer ist (bei gleichen Spulenabständen) weiße Abschnitte der Röhre werden in kürzerer Zeit durchlaufen Dicke der Peaks wird bei größerer Zeit dünner, da die Spulenabschnitte der Röhre mit immer größerer Geschwindigkeit, also in immer kürzerer Zeit, durchlaufen werden. 28.4. Radioaktiver Zerfall Materialien: - Reagenzglas für radioaktive Probe - Isotopengenerator mit Caesium137, Eluationslösung (Salzlösung zum Ausschwemmen des Ba137) - Zählrohr - Stativmaterial zum Einspannen des Reagenzglases und des Zählrohrs - Cassy - QM-Box Aufbau: - Reagenzglas über Zählrohr mit Stativmaterial aufbauen - Zählrohr an QM-Box anschließen Durchführung: - Datei e-Zerfall laden - Achtung wegen hoher Spannung: Kabel zuerst an Zählrohr, dann an QM-Box anschließen - Reagenzglas knapp über Zahlrohr Wissen: - Experiment zur Zählung von Impulsen - Halbwertszeit der Präparate sehr groß, in Schulstunde ungünstig verwende Isotopengenerator, Versuch dauert ca. 10 min - Funktionsweise des Zählrohrs wissen - Bei Zählrohr Gummikappe drauflassen, um das äußerst sensible Glimmerfenster nicht kaputt zu machen, da sonst das Gas des Zählrohrs austritt - Stabiles und instabiles Ba137 wird - Halbwertszeit von Ba137: 2,6 min - Halbwertszeit aus Wertepaaren bestimmen, dazu Werte nahe der Fit-Kurve nehmen Wähle beliebige Zerfallsrate notiere Zeit wähle die dazugehörige halbe Zerfallsrate lese Zeit ab und berechne über t2 t1 die Halbwertszeit