Formelsammlung
Werbung
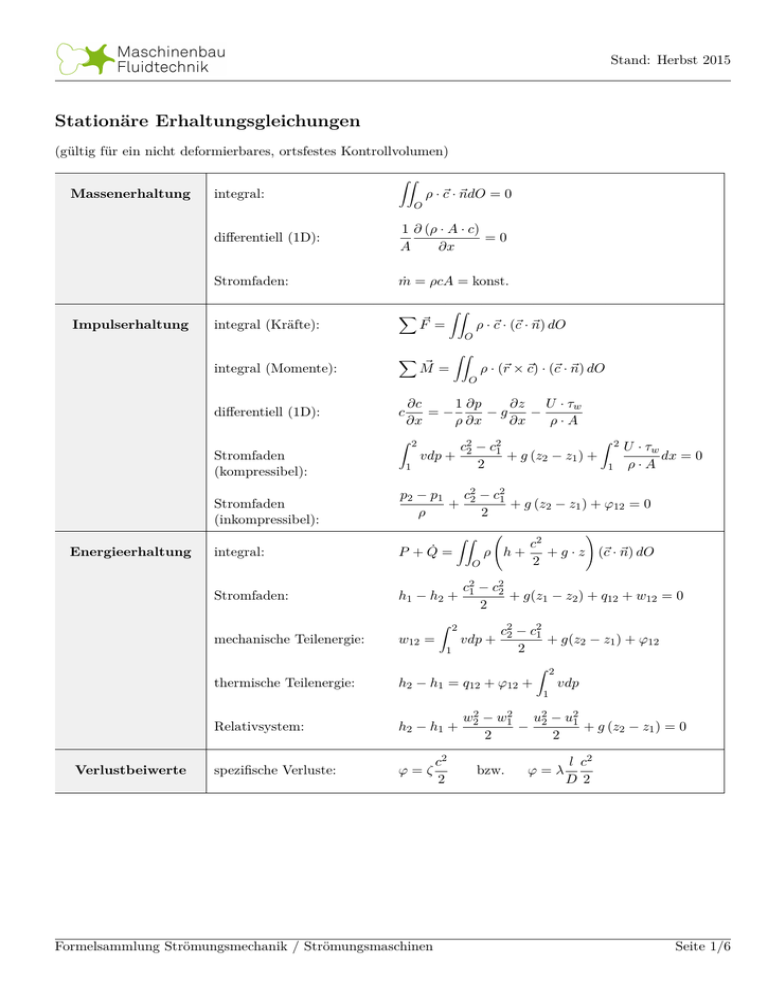
Stand: Herbst 2015 Stationäre Erhaltungsgleichungen (gültig für ein nicht deformierbares, ortsfestes Kontrollvolumen) ZZ Massenerhaltung ρ · ~c · ~ndO = 0 integral: O Impulserhaltung differentiell (1D): 1 ∂ (ρ · A · c) =0 A ∂x Stromfaden: ṁ = ρcA = konst. integral (Kräfte): X ZZ F~ = ρ · ~c · (~c · ~n) dO O integral (Momente): X ~ = M ZZ ρ · (~r × ~c) · (~c · ~n) dO O differentiell (1D): c ∂c 1 ∂p ∂z U · τw =− −g − ∂x ρ ∂x ∂x ρ·A Z 2 Stromfaden (kompressibel): Stromfaden (inkompressibel): 1 c2 − c21 + g (z2 − z1 ) + vdp + 2 2 integral: P + Q̇ = Stromfaden: h1 − h2 + w12 = dx = 0 ! c21 − c22 + g(z1 − z2 ) + q12 + w12 = 0 2 vdp + 1 thermische Teilenergie: ρ·A c2 + g · z (~c · ~n) dO ρ h+ 2 O Z 2 mechanische Teilenergie: 1 p2 − p1 c22 − c21 + + g (z2 − z1 ) + ϕ12 = 0 ρ 2 ZZ Energieerhaltung Z 2 U · τw c22 − c21 + g(z2 − z1 ) + ϕ12 2 h2 − h1 = q12 + ϕ12 + Z 2 vdp 1 Verlustbeiwerte Relativsystem: h2 − h1 + spezifische Verluste: ϕ=ζ Formelsammlung Strömungsmechanik / Strömungsmaschinen c2 2 w22 − w12 u22 − u21 − + g (z2 − z1 ) = 0 2 2 bzw. ϕ=λ l c2 D 2 Seite 1/6 Stand: Herbst 2015 Fluidstatik p = p0 + ρ · g · ∆z Grundgleichung der Hydrostatik Mechanische Zusammenhänge (schräge, ebene Wand) Druckkraft FD = (p0 + ρghS ) · A Kraftangriffspunkt yD · FD = yD · FD = Z Z y · dF y · (p0 + ρgh) dA mit h = y · sin(α) p0 α y hS FD A S D p·V =m·R·T Zustandsgleichung ideales Gas Grundgleichungen der Aerostatik p0 ρ0 · g Definition H0 = isotherm: p(z) ρ(z) − z = = e H0 p0 ρ0 polytrop: p(z) p(z) =konst. =konst. ; n ρn T n−1 p(z) n−1 z = 1− p0 n H0 n n−1 ρ(z) n−1 z = 1− ρ0 n H0 1 n−1 T (z) n−1 z = 1− T0 n H0 Formelsammlung Strömungsmechanik / Strömungsmaschinen Seite 2/6 Stand: Herbst 2015 Potentialtheorie Potentialtheorie Definition Mit der differenzierbaren, komplexen Funktion F (z) = F (x + iy) = φ + iψ folgt: φ = Re (F (z)) Potentialfunktion ψ = Im (F (z)) Stromfunktion karthesische Koordinaten cx = ∂φ ∂ψ = ∂x ∂y und cy = ∂φ ∂ψ =− ∂y ∂x Polarkoordinaten cr = ∂φ 1 ∂ψ = ∂r r ∂ϕ und cϕ = 1 ∂φ ∂ψ =− r ∂ϕ ∂r Energiewandlung in Strömungsmaschinen Definitionen 1: Laufradsaugseite ; 2: Laufraddruckseite wR = u2 · c2u − u1 · c1u = ht2 − ht1 Eulersche Grundgleichung wR = Dissipation durch Stoß Reaktionsgrad 1 2 c2 − c21 + u22 − u21 + w12 − w22 2 ϕSt = ζSt 2 wSt 2 h2 − h1 w2 − w22 + u22 − u21 wR,stat = 1 = ht2 − ht1 2 (u2 · c2u − u1 · c1u ) wR allgemeine Form: r= spezielle Form: r =1− c2u 2 · u2 für drallfreie Zu- bzw. Abströmung und konstante Meridiankomponenten Formelsammlung Strömungsmechanik / Strömungsmaschinen Seite 3/6 Stand: Herbst 2015 Wirkungsgradkette in Strömungsmaschinen ηm Pf ηu,LE Pu,LE ηv Pu,LA ηu,LA PR ηmi ηma Pi Pe ηu ηi ηe Ähnlichkeit Maßstabsfaktoren Ähnlichkeitsbeziehungen Längenmaßstab mL = D2I D2II Drehzahlmaßstab mn = nI nII Geschwindigkeitsmaßstab mG = c2I = mn · mL c2II spezifische Stufenarbeit wf wf I = m2n · m2L mit wf ∼ n2 · D22 (ηi = konst.) wf II (auch Abdrehen) Durchsatz V̇ V̇I = mn · m3L mit V̇ ∼ n · D23 (ηv = konst.) V̇II V̇I = mn · mL (Abdrehen) V̇II Innenleistung Pi PiI = m3n · m5L mit Pi ∼ n3 · D25 (ηi = konst.) PiII PiI = m3n · m3L (Abdrehen) PiII 1 − ηiI ReII = 0, 5 + 0, 5 1 − ηiII ReI Aufwertungsformel (Ackeret) 0,2 mit ReI > ReII charakteristische Länge für ReI \ReII : D2 charakteristische Geschwindigkeit ReI \ReII : u2 Formelsammlung Strömungsmechanik / Strömungsmaschinen Seite 4/6 Stand: Herbst 2015 Strömungsmechanische Kennzahlen Trägheitskraft c·l·ρ = Reibungskraft η Reynoldszahl Re = Mach-Zahl Ma = Strouhal-Zahl St = instationäre Trägheitskraft f ·l = stationäre Trägheitskraft c Froude-Zahl Fr = stationäre Trägheitskraft c2 = Schwerkraft l·g Strömungsgeschwindigkeit c = Schallgeschwindigkeit a Druckkraft p 1 Eu = = = stationäre Trägkeitskraft ρ · c2 κ · M a2 Eulerzahl (ideales Gas) Maschinenbeschreibende Kennzahlen Druckzahl ψ= |wf | Gesamtdruckänderung = u2 = f (wf , n, D2 ) Staudruck 2 2 Volumenstromzahl φ= Volumenstrom V̇ = = f V̇ , n, D 2 Bezugsvolumenstrom u2 · π4 · D22 Leistungszahl λ= V̇ · |wf | · ηi±1 Innenleistung ±1 = = φ · ψ · η = f w , V̇ , η , n, D i 2 f i u2 Bezugsleistung u2 · π4 · D22 · 22 Durchmesserzahl δ= Laufraddurchmesser D2 ψ 0,25 = = 0,5 = f wf , V̇ , n, D2 Laufraddurchmesser EM (D2 )11 φ Laufzahl Spezifische Drehzahl Drehzahl n φ0,5 σ= = = 0,75 = Drehzahl EM n11 ψ s 4 · V̇ π2 · n 2 · |wf | π 2 · n2 −0,75 = f wf , V̇ , n nq = 157, 8 · σ; [nq ] =min-1 (EM = Einheitsmaschine) Formelsammlung Strömungsmechanik / Strömungsmaschinen Seite 5/6 Stand: Herbst 2015 Symbole und Indizes Symbol Einheit Definition Symbol Einheit Definition a m·s-1 Schallgeschwindigkeit V̇ m3 · s-1 Volumenstrom A m2 Fläche w m·s-1 Relativgeschwindigkeit c m·s-1 Absolutgeschwindigkeit x, y, z m kartesische Koordinaten D m Durchmesser ζ - Verlustbeiwert f s-1 Frequenz η Pa·s dynamische Viskosität F N Kraft η - Wirkungsgrad g m·s-2 Erdbeschleunigung κ - Isentropenexponent h m2 ·s-2 spezifische Enthalpie λ - Rohrreibungszahl H m Höhe ρ kg·m-3 Dichte l m charakteristische Länge τw N·m-2 Wandschubspannung m kg Masse ϕ m2 ·s-2 spezifische Dissipation ṁ kg·s-1 Massenstrom φ m2 ·s-1 Potentialfunktion M N·m Drehmoment ψ m2 ·s-1 Stromfunktion n - Polytropenexponent n min-1 Drehzahl ~n - „nach außen“ weisender Normalenvektor Index Definition O m2 Kontrolloberfläche e effektiv p N·m-2 Druck f Fluid P W Leistung i innen q m2 ·s-2 spezifische Wärme LA Laufrad r - Reaktionsgrad LE Leitrad r, ϕ, z - Polarkoordinaten m mechanisch R J·kg-1 ·K-1 spezifische Gaskonstante R Rad t s Zeit stat statisch T K Temperatur St Stoß u m·s-1 Umfangsgeschwindigkeit t total U m Umfang u Umfangskomponente v m3 ·kg-1 spezifisches Volumen v volumetrisch V m3 Volumen I, II Maschine I, II Formelsammlung Strömungsmechanik / Strömungsmaschinen Seite 6/6