C4.6: Oberflächenintegrale Ziel: Berechnung von Integralen, deren

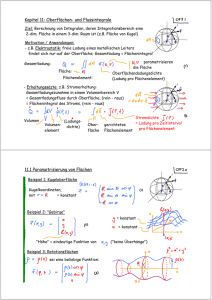
C4.6: Oberflächenintegrale
Ziel: Berechnung von Integralen, deren Integrationsbereich eine
2-dim. Fläche in einem 3-dim. Raum ist (z.B. Fläche von Kugel)
Motivation / Anwendungen:
- z.B. Elektrostatik: freie Ladung eines metallischen Leiters
findet sich nur auf der Oberfläche; Gesamtladung = Flächenintegral
Gesamtladung:
Fläche:
Flächenelement:
parametrisieren
die Fläche
Oberflächendadungsdichte
(Ladung pro Flächenelement)
- Erhaltungssäzte: z.B. Stromerhaltung:
Gesamtladungszunahme in einem Volumenbereich V
= Gesamtladungsfluss durch Oberfläche, (rein - raus)
= Flächenintegral des Stroms, (rein - raus)
Volumen
(LadungsVolumendichte)
element
Oberfläche
Stromdichte
= Ladung pro Zeitinterval
gerichtetes
pro Flächenelement
Flächenelement
Parametrisierung von Flächen
Beispiel 1: Kugeloberfläche
Kugelkoordinaten,
mit
= konstant
Beispiel 2: "Gebirge"
= konstant
= konstant
"Höhe" = eindeutige Funktion von
Beispiel 3: Rotationsflächen
sei eine beliebige Funktion:
("keine Überhänge")
Parametrisierung von Flächen in
- allgemeine Formulierung
2D-Fläche in
z.B. Oberfäche einer Kugel mit Radius R:
Anmerkung:
Jede Koordinatentransformationen in
definiert eine Flächenschar,
denn jede feste Wahl einer Koordinate liefert eine neue Fläche. Z.B:
= konstant,
[siehe Beispiel 1 auf Seite b]
Zurück zu (c.1), mit
Notationsänderung:
=konstant
(um Anzahl der Indizes
zu verringern)
= konstant
Koordinatenlinie (variere eine d. Variablen, halte andere fest) = Raumkurve
= konstant,
- Koordinatenlinie:
- Koordinatenlinie:
= konstant,
Lokalen Kurvengeschwindigkeiten (siehe ZV5a) entlang Koordinaten:
in
-Richtung:
in
-Richtung:
Flächenelement:
Betrachte das Flächenelement aufgespannt durch
und
Es wird charakterisiert durch seine Fläche,
und die Richtung eines
stehenden Einheitsvektors
zur Fläche
(ortsabhängiger "Normalvektor")
[vergleiche den rein 2-dim Fall, siehe (C4j.5); dort war
, aber hier ist
Definition: gerichtetes Flächenelement [Verallgemeinerung von (C4j.3)]
Betrag:
Richtung:
(legt auch "oben", "unten" fest)
Größe der Fläche für
:
"Fläche über C":
Lagrange-Identität (L4k.7):
mit:
Für krummlinig-orthogonale Koordinaten:
somit:
Betrag des Flächenelements:
Richtung des
Flächenelements:
Fläche über C:
ortsabhängig!)
Beispiel 1: Kugeloberfläche
Kugelkoordinaten (siehe ZV5b):
(V5m.8-10):
Einheitsvektoren sind orthonormal:
Zur Erinnerung:
(obwohl wir sie
hier nicht explizit
brauchen)
Kugeloberfläche:
Radius =
Kugel
Beispiel 2: Gebirge
(hier sind Koordinaten nicht krummlinig!)
"Höhe"
(f.2)
(
Über Bereich
wie groß ist Gebirgsoberfläche?
, also ein nicht-orthog.
Koordinatensystem)
Beispiel 3: Rotationskörper
Orthogonal:
Oberfläche des Rotationskörpers für den Bereich
-Integral ist trivial, wegen Nutzung von Symmetrie!
Verallgemeinerung: Flächenintegral einer Funktion
Sei
eine Fläche (wie bisher),
eine Funktion (auf demselben Gebiet
C definiert wie die Fläche)
und
Definition: Integral von
über C:
entlang der Fläche
über dem Gebiet
:
Interpretation: Gewichtung jedes Punktes auf der Fläche (parametrisiert durch
)
durch die Gewichtsfunktion
[z.B.
= Flächenladungsdichte, wie in (a.1) ]
Beispiel
Kugelfläche:
Anmerkung:
Vergleiche
(g.8)
ist unabhängig von der Wahl der Parametrisierung der Fläche!
[Beweis: siehe z.B. Grossmann, Mathematischer Einführungskurs in für die Physik, 2004]
C4.7 Flussintegrale durch Flächen
Sei
(siehe AD-Text, V4.2)
ein Vektorfeld.
Wieviel "fliesst" durch die Oberfläche
?
sei gerichtetes Oberflächenelement am Ort
Zerlege
in Anteile
:
zum Flächenelement
"Normalkomponente" fliesst durch Flächenelement hindurch
"Tangentialkomponente fliesst am Flächenelement entlang
Definition: "Fluss" durch
Flächenelement:
Definition: "Fluss" durch die Fläche
:
Beispiel 1: Elektrisches Feld einer Punktladung
Berechne Fluss durch Oberfläche einer Kugel mit Radius
:
Seite g:
Fluss hängt nicht vom Radius ab (!). Das ist ein Beispiel vom
Gauss-Gesetz der Elektrostatik: Der durch die Oberfläche
eines Volumens
hindurchtretende Fluss
des elektrischen Feldes ist proportional zur gesamten in
enthaltenen elektrischen Ladung:
Beispiel 2: Fluss eines Magnetfelds durch Zylinder
Magnetfeld sei
Fluss nach aussen durch den Boden:
Deckel
Mantel
Boden
Fluss nach aussen durch den Deckel:
Fluss nach aussen durch den Mantel:
Fluss nach aussen durch ganzen Zylinder:
Beispiel für allgemeines Gesetz: Magnetfeldfluss durch geschlossene Fläche = 0 !
Zusammenfassung: V4.2 Flächen- und Flussintegrale
Gerichtetes
Flächenelement:
"Fluss" durch
Flächenelement:
"Fläche über G":
"Fluss" durch
die Fläche
:
Für orthogonale Koordinaten:
Betrag des Flächenelements:
Richtung:
Fläche über C: