Aufgaben Terme V (Terme mit Brüchen) 1. Bestimmen Sie die

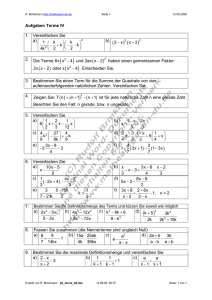
MON
Seite 1
06.09.2012
Aufgaben Terme V (Terme mit Brüchen)
1. Bestimmen Sie die maximale Definitionsmenge und vereinfachen Sie.
a) 1
b) 4x
3 ab
10x



2a 4a
ab
x 1 2  x
c) 1 2 2k  x
d)
k k  3 
 
k3
k x
kx
k 3
e)
f)
1
1
2
3x
2
6

 2
4


2
2
1 k 1 k k  1
 x  2 x  2  2  x 
2. Bestimmen Sie die maximale Definitionsmenge.
Vereinfachen Sie soweit wie möglich.
a) x
b) k k

4 3
23
3k k
k k

4 3
d)
e)
1
1
k k  2

k 2
1 1
k 1
 k k 1
2
2 2
3. Zeigen Sie die Gleichheit.
a) 2  k
1
für k  1
 k  1 k 
1 k
1 k
c)
x
k  4x
2k k 2
f)
x
1
: 2
x 1 x  x
b)  k  1  
k  1
1 2  :  k  2   1

 

4. Bestimmen Sie die maximale Definitionsmenge für die Variable x
und vereinfachen Sie.
a) 3x 2  3 2x  2
b)
c) ax 2  2x
2x  1
x 2  2x  1 
;

2x  2
ax  2x 2
x 2  3x x  3


5. Zeigen Sie die Gleichheit der beiden Terme.
a) 2x 2  3x  1
b) 2
3
3
x  x  1
;
; 2x  1 
x 1
x2
x2
6. Welche Terme sind äquivalent (gleichwertig)?
1)
2)
4 2
3x  2x  1
x 3  6x 2
3
12x 2  3


x 2  8x
x 3
 3a  5 
x2  3  x  x  3 
6)
 4  x  x  x2
9)
9x2  x 4
12)
9xy  y  2x 
9xy2  18x2y
5)
7)
9a2  30a  25
8)
10)
x2  3  x   2x3  x2
11)
x
2x  1
13)
4x2  8x 4
14)
 xy  x 
16)
4x
17)
x2  4  x 
Erstellt von E.Mönig
x3  2
x 1
3)
4)
2
2
06.09.12 16:35
15)
18)
a0
x 5
15
x3
x 2  y  1
2
Seite: 1 von 1