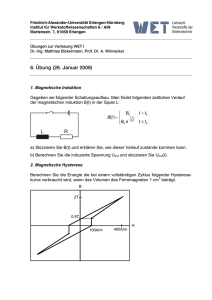
Die magnetische Induktion

Musso: Physik II
Teil 28 Magnetische Induktion
Seite 1
ELEKTRIZITÄT UND MAGNETISMUS
Tipler-Mosca
28. Die magnetische Induktion (Magnetic induction)
28.1 Der magnetische Fluß (Magnetic flux)
28.2 Induktionsspannung und Faraday'sches Gesetz (Induced EMF and Faraday's law)
28.3 Die Lenz'sche Regel (Lenz's law)
28.4 Induktion durch Bewegung (Motional EMF)
28.5 Wirbelströme (Eddy currents)
28.6 Induktivität (Inductance)
28.7 Die Energie des Magnetfelds (Magnetic energy)
28.8 RL-Stromkreise (RL circuits)
28.9 Magnetische Eigenschaften von Supraleitern (Magnetic properties of superconductors)
Magnetische Induktion: Ein zeitlich veränderliches Magnetfeld kann einen Strom erzeugen, wenn sich der
magnetische Fluß durch eine Fläche ändert, die von einer geschlossenen, unbewegten Leiterschleife begrenzt ist.
Universität Salzburg
Seite 1
29.04.2007
Musso: Physik II
Universität Salzburg
Teil 28 Magnetische Induktion
Seite 2
Seite 2
29.04.2007
Musso: Physik II
28.1 Der magnetische Fluß (Magnetic flux)
Teil 28 Magnetische Induktion
Seite 3
Mit dA ein Flächenelement der Fläche A und nˆ der zugehörige Normalvektor ⇒
Magnetischer Fluß Φ mag = ∫ B ⋅ dA = ∫ Bn ⋅ dA
A
A
SI-Einheit: 1 Weber (Wb), 1 Wb = 1 T m2
Der magnetische Fluß durch ein Flächenelement ist proportional zur Anzahl der Feldlinien,
die dieses durchsetzen
Sei A eine ebene Fläche und B über der gesamten Fläche A homogen (Betrag und Richtung konstant) ⇒
Φ mag = B ⋅ A = BA cos θ = Bn A;
für eine Spule mit N Windungen ⇒ Φ mag = N B ⋅ A = NBA cos θ = NBn A
Beispiel 28.1: Magnetischer Fluß durch eine Spule
Zylinderspule, Länge L = 40 cm, mit N = 600 Windungen mit Radius r = 2.5 cm.
Gesucht: magnetischer Fluß Φ mag bei einem Strom durch die Spule von I = 7.5 A ⇒
mit Gl. (28.3) Φ mag = NBA und Gl. (27.9) B = μ0
mit A = π r
2
⇒ Φ mag
Universität Salzburg
N
I
L
⇒ Φ mag = N μ0
N2
= μ0
Iπ r 2 = 4π × 10−7 T m A -1
L
(
( 600 )
N
N2
IA = μ0
IA ⇒
L
L
2
) ( 0.40 m ) ( 7.5 A ) π ( 0.025 m )
Seite 3
2
= 1.66 × 10 −2 Wb
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
28.2 Induktionsspannung und Faraday'sches Gesetz (Induced EMF and Faraday's law)
Seite 4
Ändert sich Φ mag durch die Leiterschleife, so wird in der Schleife eine Spannung
Uind = −
dΦmag
induziert, die über des gesamten Kreis der Leiterschleife verteilt ist.
dt
Urheber der Induktionsspannung ist ein nichtkonservatives, tangential zur Schleife
gerichtetes elektrisches Feld E
Elektrische Felder von ruhenden elektrischen Ladungen nennt man konservativ
⇒ Umlaufintegral
∫ E ⋅d
=0
C
Ein zeitlich veränderliches Magnetfeld erzeugt hingegen ein nichtkonservatives
elektrisches Feld Uind =
∫ E ⋅d = −
C
dΦ mag
dt
=−
d
B ⋅ dA
dt ∫A
Zur Vorzeichenvereinbarung: positive Richtung tangential zum Integrationsweg C
ist mit der Richtung von nˆ durch eine Rechte-Hand-Regel verknüpft ⇒
ist
Universität Salzburg
dΦ mag
dt
positiv, dann zeigt E tangential zu C in negativer Richtung
Seite 4
29.04.2007
Musso: Physik II
Beispiel 28.2: Induktionsspannung in einer kreisrunden Spule I
Teil 28 Magnetische Induktion
Seite 5
Längsachse einer kreisrunden Spule mit N = 400 Windungen und Radius r = 4 cm schließt mit Richtung eines
homogenen äußeren Magnetfeldes einen Winkel θ =30° ein. Die Feldstärke nimmt pro Sekunde um 85 T zu
(ohne Richtungsänderung). Gesucht: die in der Spule induzierte Spannung Uind ⇒
mit Gl. (28.4) Uind = −
Uind = −
dΦ mag
dt
=−
dΦ mag
dt
und mit Gl. (28.3) Φ mag = NB ⋅ A = NBA cos θ
⇒
(
)
2
d
dB
dB
= −Nπ r 2 cos θ
= − ( 400 ) π ( 0.04 m ) cos 30° 85 T s-1 =
(NBA cosθ ) = −NA cosθ
dt
dt
dt
= −111 V
Beispiel 28.3: Induktionsspannung in einer kreisrunden Spule II
mögliches Prüfungsbeispiel
Universität Salzburg
Seite 5
29.04.2007
Musso: Physik II
Beispiel 28.4: Ein nichtkonservatives induziertes elektrisches Feld
Teil 28 Magnetische Induktion
Seite 6
mögliches Prüfungsbeispiel
Universität Salzburg
Seite 6
29.04.2007
Musso: Physik II
28.3 Die Lenz'sche Regel (Lenz's law)
Teil 28 Magnetische Induktion
Das negative Vorzeichen im Faraday'schen Gesetz Uind = −
Induktionsspannung Uind
Seite 7
dΦ mag
ergibt sich aus der Richtung der
dt
⇔ Lenz'sche Regel: allgemeines physikalisches Prinzip
Stabmagnet bewegt sich nach rechts ⇒
im leitenden Ring wird eine Spannung Uind
induziert ⇒ es fließt ein Strom ⇒ es wird
ein Magnetfeld erzeugt, das auf den
Stabmagneten eine Kraft ausübt, die der
Annäherung entgegenwirkt
Universität Salzburg
Seite 7
29.04.2007
Musso: Physik II
Beispiel 28.5: Lenz'sche Regel und Induktionsstrom
Teil 28 Magnetische Induktion
Seite 8
Ermittlung der Richtung des Induktionsstromes unter Zuhilfenahme der alternativen Formulierung
der Lenz'schen Regel
Änderung ΔB1 des Magnetfeldes B1 durch Annäherung des Stabmagneten
Anwendung der alternativen Formulierung
Aus der Richtung von B2 ⇒ mit Hilfe der
der Lenz'schen Regel; B2 Magnetfeld des
Rechte-Hand-Regel ⇒ Richtung des im
im Ring induzierten Stromes
Ring induzierten Stromes
Universität Salzburg
Seite 8
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Seite 9
Ring bewegt sich vom ruhenden Stabmagneten weg ⇒
der induzierte Strom erzeugt ein magnetisches Moment so,
daß eine Anziehung zwischen Ring und Magnet bewirkt ⇒
wirkt der relativen Bewegung entgegen
Zwei induktiv gekoppelte Stromkreise: Ein Änderung des Stroms I1 im Stromkreis 1 bewirkt eine Änderung
des magnetischen Flusses im Stromkreis 2, und induziert eine Spannung Uind,2 bzw. einen Strom I2 .
Der Strom I2 versucht der Flußänderung entgegenzuwirken.
Selbstinduktion: ändert sich der Strom in der Spule, so wird in der Spule eine
große Spannung induziert, die der Flußänderung entgegenzuwirken sucht
Die Selbstinduktion ist dafür verantwortlich, daß der Strom in einem
Stromkreis nicht sprunghaft ansteigen oder abfallen kann.
Universität Salzburg
Seite 9
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Beispiel 28.6: Anwendung der Lenz'schen regel bei einer bewegten Spule
Seite 10
Rechteckige Spule mit N = 80 Windungen und Seitenlängen a = 20 cm und b = 30 cm; Hälfte der Spule in
einem Magnetfeld mit B = 0.8 T; Widerstand der Spule R = 30 Ω;
gesucht: Betrag und Richtung des induzierten Stromes, wenn die Spule sich mit einer Geschwindigkeit
v = 2 m s-1 a) nach rechts, b) nach oben, c) nach unten bewegt
Uind
und mit
dt
R
= NB ⋅ A = NBax ⇒ die Spule bewegt sich nach rechts ⇒
Teil a) aus Gl. (28.4) Uind = −
Gl. (28.3) Φ mag
dΦ mag
dt
dΦ mag
⇒
mit I =
=0 ⇒ I =0
dΦ mag
U
d
dx
NBa dx
⇒ I = ind =
=
( NBax ) = NBa
dt
dt
dt
R
R dt
( 80 )(0.8 T )(0.2 m )
=
2 m s-1 = 0.853 A, aufgrund der Lenz'schen Regel
( 30 Ω )
Teil b) mit
=
(
)
in der alternativen Formulierung ⇒ der induzierte Strom ruft einen magnetischen
Fluß durch diesselbe Fläche hervor, der seiner Ursache entgegengesetzt gerichtet
ist ⇒ der indizierte Strom fließt entgegengesetzt der Uhrzeigerrichtung
dΦ mag
U
d
dx
NBa dx
⇒ I = ind =
=
(NBax ) = NBa
dt
dt
dt
R
R dt
( 80 )(0.8 T )(0.2 m )
2 m s-1 = 0.853 A, aufgrund der Lenz'schen Regel
=
( 30 Ω )
Teil c) mit
=
(
)
in der alternativen Formulierung ⇒ der induzierte Strom ruft einen magnetischen
Fluß durch diesselbe Fläche hervor, der seiner Ursache entgegengesetzt gerichtet
ist ⇒ der indizierte Strom fließt in Uhrzeigerrichtung
Universität Salzburg
Seite 10
29.04.2007
Musso: Physik II
28.4 Induktion durch Bewegung (Motional EMF)
Teil 28 Magnetische Induktion
Seite 11
Wird ein Leiter in einem Magnetfeld bewegt, so wird eine Spannung induziert
Beispiel 28.7: Durch eine Flipspule fließende Ladung
Die Ebene einer Spule mit N Windungen sei senkrecht zur Richtung eines homogenen, statischen
Magnetfeldes B. Gesucht: die Ladung Q, die durch die Spule fließt bei Umdrehung um 180°
dq
aus Gl. (25.1) I =
⇒ dq = Idt , aus Uind = IR ⇒ Uind dt = IRdt = Rdq,
dt
dΦ mag
1
⇒ Uind dt = − dΦ mag ⇒ − dΦ mag = Rdq ⇒ dq = − dΦ mag
aus Gl. (28.4) Uind = −
R
dt
Φ mag,f
Q
ΔΦ mag
1
1
Q = ∫ dq = −
dΦ mag = − ( Φ mag,f − Φ mag,i ) = −
,
∫
R
R
R
Φmag,i
0
mit Gl. (28.3) Φ mag = NB ⋅ A ⇒
(
⇒
⇒
)
ΔΦ mag = Φ mag,f − Φ mag,i = NB ⋅ Af − NB ⋅ Ai = NB ⋅ Af − Ai =
(
)
2NAB
= NAB ⋅ −nˆ − nˆ = −2NAB ⇒ Q =
R
Universität Salzburg
Seite 11
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Seite 12
In einem umgebenden homogenen Magnetfeld gleitet ein elektrisch
leitender Stab auf leitende Scheinen, die über einen Widerstand
verbunden sind.
Magnetischer Fluß Φ mag = B ⋅ A = BA = B x ⇒ bewegt sich der
Stab um dx ⇒ Zunahme des Flächeninhaltes um dA = dx ⇒
Zunahme von Φ mag : dΦ mag = B dx ⇒ Änderungsrate
dΦ mag
dx
= B v ⇒ induzierte Spannung Uind = −B v
dt
dt
induziertes elektrisches Feld ist entgegengesetzt dem Uhrzeigersinn gerichtet.
=B
⇒
Überprüfung durch Lenz'sche Regel: Strom wird durch Bewegung des Stabes nach rechts induziert ⇒
der induzierte Strom ruft eine magnetische Kraft FL hervor, die nach links gerichtet ist: FL = I × B
wegen Gl. (26.4).
Andere Betrachtungsweise: Ladungsträger nach rechts bewegt mit v
⇒ Kraft auf Ladungsträger
FU = qv × B.
Mit v d Driftgeschwindigkeit der positiven Ladungsträger ⇒
magnetische Kraft FL = qv d × B ⇒ Ladungstrennung ⇒
Entstehung eines nach rechts gerichteten elektrischen
Feldes E⊥
⇒ Kraft FR = qE⊥ nach rechts auf die
Ladungsträger
⇒ Summe FL + FR muss null sein;
Bewegung der Ladungsträger mit dem Stab ⇒
⇒ aufwärts gerichtete Kraft FU = qv × B ⇒ die insgesamt an einem Ladungsträger verrichtete Arbeit:
FU
=qv B
Universität Salzburg
⇒ Arbeit pro Ladungseinheit = Spannung = Uind = v B
Seite 12
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Seite 13
Die auf einen positiven Ladungsträger in einem leitenden Stab, der mit
konstanter Geschwindigkeit in einem homogenen Feld bewegt wird,
wirkende magnetische Kraft besitzt eine nach aufwärts gerichtete
Komponente ⇒ alle positiven Ladungsträger werden nach oben
gedrückt ⇒ Ladungstrennung ⇒ Aufbau eines elektrischen Feldes
E
⇒ im Gleichgewicht qE = qvB ⇒ E = vB ⇒ Potentialdifferenz
U = E = vB
wenn kein Strom durch den Stab fließt, bzw.
U = vB − IR wenn ein Strom durch den Stab fließt.
Beispiel 28.8: Ein U-förmiger Leiter und ein gleitender Stab
Elektrisch leitender Stab, = 0.15 m, gleitet mit Geschwindigkeit v = 8 m s-1 in einem Magnetfeld B = 0.6 T
auf Schienen, die über einen Widerstand R = 25 Ω miteinander verbunden sind.
Gesucht: a) induzierte Spannung Uind , b) induzierter Strom I,
c) die erforderliche Kraft, um den Stab zu bewegen, d) die
umgesetzte Leistung ⇒
(
)
Teil a) Uind = vB = 8 m s-1 ( 0.6 T )( 0.15 m ) = 0.720 V,
Teil b) I = Uind /R = ( 0.720 V ) / ( 25 Ω ) = 28.8 mA,
Teil c) aus Gl. (26.4) F = I B = ( 28.8 mA )( 0.15 m )( 0.6 T ) = 2.59 mN,
Teil d) P = IR 2 = ( 28.8 mA )( 25 Ω ) = 20.7 mW
2
Universität Salzburg
Seite 13
29.04.2007
Musso: Physik II
Beispiel 28.9: Magnetische Reibung
Teil 28 Magnetische Induktion
Seite 14
mögliches Prüfungsbeispiel
Allgemeine Gleichung für eine durch die Bewegung induzierte Spannung auf ein Leiterelement d bewegt
mit Geschwindigkeit v
Beispiel 28.10: Überprüfung der Beziehung U ind=vBL
Zu zeigen: aus Gl. (28.8) ⇒ induzierte Spannung durch Gl. (28.6) gegeben:
Uind =
∫(
)
v ×B d =
C
∫(
)
vr × B d +
C1
∫(
)
0×B d =
C2
mit v r × B = v r ex × Bey = v r Bez und d = d ez
(v
r
)
× B d = v r Bd
∫ (v
b
Uind =
a
r
)
∫ (v
b
r
)
×B d
a
⇒
⇒
b
b
a
a
× B d = ∫ v r Bd = v r B ∫ d = v r B
Universität Salzburg
Seite 14
29.04.2007
Musso: Physik II
28.5 Wirbelströme (Eddy currents)
Teil 28 Magnetische Induktion
Seite 15
Ändert sich das Magnetfeld, in dem sich der Metallstab befindet, so
wird entlang jedes geschlossenen Weges innerhalb des Stabes
eine Spannung induziert ⇒ es fließen die sogenannten Wirbelströme
Wirbelströme erzeugen Wärme ⇒ Energieverluste;
Beispiel: Wirbelströme im Kern einer Transformatorspule ⇒ Energieverlust im Transformator
Ein Metallblech wird schnell durch das Magnetfeld nach rechts
gezogen ⇒ der magnetische Fluß durch die Schleife C
nimmt ab ⇒ es wird ein elektrisches Feld im Uhrzeigersinn
aufgebaut ⇒ auf den induzierten Strom wirkt eine Kraft nach links
In der Regel sind Wirbelströme unerwünscht ⇔ Leistungsverlust in Form
von Joule'sche Wärme ⇒ damit Verluste möglichst klein ⇒ Erhöhung
des elektrischen Widerstandes der Wege, entlang derer Wirbelström e
induziert werden ⇒ Verwendung von isolierten Blechen, von Schlitzen
Anwendungen von Wirbelströmen:
zur Dämpfung von Oszillationen, z.B. bei empfindlichen mechanischen Waagen,
Wirbelstrombremsen in Fahrzeugen
Universität Salzburg
Seite 15
29.04.2007
Musso: Physik II
28.6 Induktivität (Inductance)
Teil 28 Magnetische Induktion
Seite 16
Eine Spule werde durch einen Strom I durchflossen ⇒ der Strom I erzeugt ein Magnetfeld B proportional zu I
⇒ der magnetische Fluß durch die Spule ist proportional zu I ⇒
Φ mag = LI wobei L Selbstinduktivität der Spule
⇔ 1H = 1
SI-Einheit der Induktivität: Henry (H)
Wb
T m2
=1
A
A
Berechnung der Selbstinduktivität einer Zylinderspule mit N Windungen und Länge , in der ein Strom I fließt:
aus Beispiel 28.1 ⇒ magnetischer Fluß durch eine Zylinderspule Φ mag =
L=
Φ mag
I
μ0 N 2IA
2
⎛N ⎞
= μ0 ⎜ ⎟ IA = LI
⎝ ⎠
⇒
2
⎛N ⎞
= μ0 ⎜ ⎟ A
⎝ ⎠
Selbstinduktivität ∼
( Windungsdichte )
2
bzw.
Selbstinduktivität ∼ Volumen der Zylinderspule
2
⎛N ⎞
aus Gl. (28.11) L = μ0 ⎜ ⎟ A
⎝ ⎠
⇒ μ0 =
L
2
⎛N ⎞
⎜ ⎟ A
⎝ ⎠
⇒ SI-Einheiten eigesetzt
H
= H m-1
−2
−2
m ⋅m ⋅m
Beispiel 28.11: Selbstinduktivität einer Zylinderspule
Zylinderspule,
= 10 cm, N = 100, A = 5 cm2 , gesucht: Selbstinduktivität ⇒
aus Gl. (28.11) L =
Universität Salzburg
Φ mag
I
2
⎛N ⎞
⎛ 100 ⎞
= μ0 ⎜ ⎟ A = 4π × 10−7 H m-1 ⎜
⎟
⎝ ⎠
⎝ 0.10 m ⎠
(
)
Seite 16
2
( 5.0 × 10
−4
m2
) ( 0.10 m) = 6.28 × 10
−5
H
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Seite 17
Ändert sich die Stromstärke I in einem Stromkreis ⇒ der magnetische Fluß Φmag ändert sich ⇒
eine Spannung Uind wird induziert
dΦmag
dt
=
d ( LI )
dt
=L
dI
dt
⇒ Selbstinduktivität L des Stromkreises konstant ⇒
⇒ mit Gl. (28.4) Uind = −
dΦ mag
dt
= −L
dI dI
∼
dt dt
Spulen mit größerer Selbstinduktivität L werden oft als Induktivitäten bezeichnet.
Sei R der Innenwiderstand einer Spule ⇒ Spannungsabfall UL an der Spule
UL = Uind − IR = −L
dI
− IR
dt
Gegeninduktion
Zwei benachbarte Stromkreise mit Strömen I1 und I2 ⇒ das Magnetfeld über die Fläche A2 ergibt sich als
Überlagerung der von I1 und I2 erzeugten Magnetfeldern B1 ∼ I1 und B2 ∼ I2
⇒
Fluß Φ mag,2,1 von B1 durch den Kreis 2: Φ mag,2,1 = L2,1I1 wobei L2,1 Gegeninduktivität der beiden Stromkreise
Universität Salzburg
Seite 17
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Seite 18
Berechnung der Gegeninduktivität zweier eng gewickelter, konzentrisch angeordneter Zylinderspulen, die innere mit
Radius r1 und Windungszahl N1, und die äußere mit r2 und N2 .
2
Durch die innere Zylinderspule fließe der Strom I1 ⇒ innerhalb der innere Zylinderspule B1 = μ0
(
)
N1
I1, gilt für
r < r1. Außerhalb Magnetfeld B1 vernachlässigbar schwach ⇒ Φ mag,2,1 = N2 B1 A1 = N2 B1 π r12 = N2 μ0
=
N2
μ0
N1
(
)
I1 π r12 = L2,1I1 ⇒ L2,1 =
Φ mag,2,1
I1
= μ0
N2 N1
N1
(
)
I1 π r12 =
(π r )
2
1
Tesla-Spule als Transformator (siehe Teil 29.7): Eine niedrige Wechselspannung
in der äußeren Spule wird in eine höhere Wechselspannung in der inneren
umgewandelt.
http://de.wikipedia.org/wiki/Tesla-Transformator
Universität Salzburg
Seite 18
29.04.2007
Musso: Physik II
28.7 Die Energie des Magnetfelds (Magnetic energy)
Teil 28 Magnetische Induktion
Seite 19
Eine Spule (Induktivität) speichert magnetische Energie:
Reihenschaltung eines Widerstands R und einer Spule L (mit vernachlässigbarem Innenwiderstand) mit einer
Spannungsquelle U0 über einen Schalter S ⇒ Schalter offen ⇒ es fließt kein Strom;
Schalter geschlossen ⇒ Strom I fließt ⇒ mit Kirchhoff'sche Maschenregel (Teil 25.5) U0 − IR − L
dI
=0 ⇒
dt
dI
wobei U0 I = die von der Batterie gelieferte Leistung, I 2 R = Leistung bzw. umgesetzte Wärme
dt
dEmag
dI
am Widerstand ⇒ mit Emag = in die Spule fließende Energie ⇒
= LI
⇒ d Emag = LId I ⇒
dt
dt
U0 I = I 2 R − LI
Emag = ∫ dEmag
If
1
= ∫ LIdI = LI 2
2
0
If
=
0
1 2
LIf = in der Spule gespeicherte Energie
2
Für eine lange Zylinderspule: aus Gl. (27.9) B = μ0
N
2
⎛N ⎞
I und mit Gl. (28.11) L = μ0 ⎜ ⎟ A
⎝ ⎠
2
⎛ B ⎞
1
1 ⎛N⎞
1 ⎛N ⎞
B2
=
Emag = LI 2 = μ0 ⎜ ⎟ A I 2 = μ0 ⎜ ⎟ A ⎜
A
⎟
2
2 ⎝ ⎠
2 ⎝ ⎠
μ
2
μ
N
0
⎝ 0 ⎠
B2
Volumen ⇒ Energiedichte des Magnetfeldes w mag =
2μ0
2
2
⇒
⇒ mit A
das von der Spule umschlossene
gilt allgemein
Universität Salzburg
Seite 19
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Seite 20
Beispiel 28.12: Energiedichte eines elektromagnetischen Felds
In einem bestimmten Gebiet des Raumes Überlagerung eines homogenen Magnetfeldes, B = 0.02 T,
und eines homogenen elektrischen Feldes E = 2.5 × 10 6 N C-1;
gesucht: a) die Energiedichte des elektromagnetischen Feldes w em = w el + w mag , b) die Energie E in einem kubischen
= 12 cm ⇒
Volumen mit der Kantenlänge
Teil a) aus Gl. (24.13) w el =
(
1
1
ε 0 E 2 = 8.85 × 10 −12 C2 N-1 m-2
2
2
(0.02 T )
B2
=
=
= 159 J m-3 ,
-2
−7
2μ0 2 4π × 10 N A
)( 2.5 × 10
6
N C-1
)
2
= 27.7 J m-3 ,
2
aus Gl. (28.20) w mag
Teil b) E = w emV = w em
Universität Salzburg
(
3
(
= 187 J m-3
)
) ( 0.12 m )
3
w em = w el + w mag = 187 J m-3 ;
= 0.323 J
Seite 20
29.04.2007
Musso: Physik II
28.8 RL-Stromkreise (RL circuits)
Teil 28 Magnetische Induktion
Seite 21
Reihenschaltung eines Widerstands R und einer Spule L (mit vernachlässigbarem Innenwiderstand) mit einer
Spannungsquelle U0 über einen Schalter S ⇒ Schalter offen ⇒ es fließt kein Strom;
bei t = 0 Schalter geschlossen ⇒ bei t > 0 Strom I fließt ⇒ mit Kirchhoff'sche Maschenregel (Teil 25.5)
U 0 − IR − L
dI
= 0 ⇒ bei t = 0 ist I (t = 0) = 0 ⇒
dt
nimmt langsamer zu als zum Zeitpunkt t = 0
dI
dt
=
t =0
U0
dI U0 IR
⇒ für t > 0
=
−
dt
L
L
L
⇔ der Strom I
U 0 If R
dI
=0 ⇒
=
dt
L
L
⇒ Endwert des Stromes wenn
⇒ If =
U0
R
RL-Stromkreis
dI U0 IR
=
−
aus
L
L
dt
1
⇒ dI = (U0 − IR ) dt
L
Substitution U0 − IR = a ⇒ − RdI = da
R
ln (U0 − IR ) − ln (U0 ) = − t
L
U
I= 0
R
R
− t
⎛
⎜1− e L
⎝
⎞
⎟ = If
⎠
Universität Salzburg
⇒
⇒
1
−
R
⎛ U − IR ⎞
R
⇒ ln ⎜ 0
⎟=− t
L
⎝ U0 ⎠
R
− t ⎞
⎛
⎜1− e L ⎟
⎝
⎠
I
dI
1
= dt
U0 − IR L
U0 −IR
∫
U0
⇒
t
dI
1
⇒ Integration ∫
= ∫ dt
U0 − IR 0 L
0
t
da
1
= ∫ dt
a
L
0
⇒
R
− t
U0 − IR
=e L
U0
U0 −IR
ln a U
0
Seite 21
t
R
=− t
L 0
⇒ U0 − IR = U0 e
L
induktive Zeitkonstante I = I f
⇒ mit τ =
R
⇒
⇒
−
R
t
L
⇒
t
− ⎞
⎛
τ
⎜1− e ⎟
⎝
⎠
29.04.2007
Musso: Physik II
Beispiel 28.13: Stromstärke in einer Spule
Teil 28 Magnetische Induktion
Seite 22
Spule mit Selbstinduktivität L = 5 mH und Widerstand R = 15 Ω wird verbunden mit Spannungsquelle U0 = 12 V.
Gesucht: a) maximale Stromstärke If , b) Zeitkonstante τ , c) Zeitdauer bis 99%If erreicht wird ⇒
t
t
− ⎞
⎛
U0
dI f
1 −τ
τ
oder aus Gl. (28.23) I = I f ⎜ 1 − e ⎟ und
Teil a) aus Gl. (28.22) If =
= 0 ⇒ If e = 0 ⇒ t = ∞ ⇒
d
τ
R
t
⎝
⎠
U
12 V
= 0.800 A,
I ( t = ∞ ) = If = 0 =
R 15 Ω
L 5 mH
Teil b) aus Gl. (28.24) τ =
=
= 333 μ s
R 15 Ω
t
t
t
− ⎞
−
−
⎛
⎛
⎛
I
I
t
I ⎞
I ⎞
τ
τ
τ
= 1− e
⇒ e = 1−
⇒ − = ln ⎜ 1 − ⎟ ⇒ t = −τ ln ⎜ 1 − ⎟
Teil c) aus Gl. (28.23) I = If ⎜ 1 − e ⎟ ⇒
If ⎠
τ
If
If
If ⎠
⎝
⎝
⎝
⎠
⇒ t = −τ ln (1 − 0.99 ) = −τ ln ( 0.01) = τ ln (100 ) = 4.61τ = 1.53 ms
RL -Stromkreis mit unterbrechungslosem Umschalter
Schutzwiderstand
unterbrechender Umschalter
Universität Salzburg
Seite 22
unterbrechungsloser Umschalter
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Zu Beginn Schalter in Position e ⇒ Maximalstrom I0 =
Seite 23
U0
; zum Zeitpunkt t = 0 Schalter auf Position f
R1 + R
umgelegt ⇒ Betrachtung des Stromkreises abcdfa ⇒ mit Kirchhoff'sche Maschenregel (siehe Teil 25.5)
dI
dI
−IR − L
=0 ⇒ L
= −IR
dt
dt
R
lnI '− ln I0 = − t '
L
R
dI
⇒ Variablentrennung
= − dt
I
L
⇒ für beliebigen Zeitpunkt t ' = t mit I ' = I
I'
t'
R
dI
⇒ Integration ∫
= − ∫ dt
I
L0
I0
⇒ I = I0 e
−
⇒
R
t
L
Beispiel 28.14: Wärmeerzeugung am Widerstand
Gesucht: Energieumwandlung am Widerstand R wenn Spulenstrom von I0 auf 0
dEel
abfällt ⇒ umgesetzte Leistung P = I R =
dt
2
mit Gl. (28.26) I = I0 e
R
− t
L
∞
⇒ Eel = ∫ I02 Re
R
−2 t
L
0
∞
⇒
∫e
0
−2
R
t
L
L
dt = −
2R
Integration siehe auch
−∞
x
∫ e dx = −
0
L x
e
2R
0
=−
⇒ dEel = I R dt
⇒ Eel = ∫ I 2 R dt
⇒
0
∞
dt = I02 R ∫ e
R
−2 t
L
dt
⇒ mit Substitution x = −2
0
L
L
( 0 − 1) =
2R
2R
⇒ Eel = I02 R
R
L
dx
t und dt = −
2R
L
1
L
= I02 L
2R 2
http://www.mathe-online.at
Beispiel 28.15: Anfangsstrom und Maximalstrom
Universität Salzburg
−∞
∞
2
mögliches Prüfungsbeispiel
Seite 23
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
28.9 Magnetische Eigenschaften von Supraleitern (Magnetic properties of superconductors)
Seite 24
Der elektrische Widerstand supraleitender Materialien ist unterhalb einer materialabhängigen kritischen Temperatur
Tc (Sprungtemperatur) null. Tc ist in Anwesenheit eines Magnetfeldes, B ≠ 0, niedriger als Tc bei B = 0.
Wird eine kritische Feldstärke Bc überschritte, dann kann das Material nicht mehr supraleitend sein
Der Meißner-Ochsenfeld-Effekt
Meißner-Ochsenfeld-Effekt: Supraleiter in einem Magnetfeld auf Temperaturen unter Tc abgekühlt ⇒
das Magnetfeld innerhalb des Materials wird null ⇔ an der Oberfläche des Supraleiters werden Supraströme
induziert, die ihrerseits ein dem äußeren Magnetfeld entgegengerichtetes Magnetfeld erzeugen.
Meißner-Ochsenfeld-Effekt
in supraleitendem Zinn
Magnetisches Schweben (Levitation) aus der Abstoßung
zwischen Magnetfeld des Permanentmagneten und Magnetfeld
erzeugt von den induzierten Strömen im Supraleiter
Universität Salzburg
Seite 24
29.04.2007
Musso: Physik II
Teil 28 Magnetische Induktion
Seite 25
In Typ-I-Supraleiter tritt ein vollständiges Meißner-Ochsenfeld-Effekt: für Baus = Bapp < Bc ⇒ μ0 M = −Baus ,
Bc sehr klein ⇒ Materialien nicht geeignet als Wicklungen supraleitender Magneten.
In Typ-II-Supraleiter beginnt das Magnetfeld bei Bc,1 zu durchdringen, jedoch bleibt das Material bis Bc,2
supraleitend, Materialien sind Legierungen oder Metalle, die im normalleitenden Zustand einen großen
Widerstand besitzen ⇒ Materialien geeignet als Wicklungen supraleitender Magneten.
Die Flußquantisierung
Betrachtung eines stromdurchflossenen supraleitenden Ring mit Fläche A ⇒ Strom im Ring erzeugt
einen magnetischen Fluß Φ mag = Bn A; Flußänderung ⇒ Spannung induziert ⇒ beim Supraleiter ist
der elektrische Widerstand gleich null ⇒ die induzierte Spannung würde einen unendlichen Fluß
bewirken ⇒ tatsächlich ist im Supraleiter Φ mag "eingefroren"
h
mit n = 1,2,3,...
2e
h
=
= 2.0678 × 10 −15 T m2
2e
quantenmechanische Behandlung ⇒ Φ mag = n
kleinste Einheit: Flußquant oder Fluxon Φ mag,0
Universität Salzburg
Seite 25
29.04.2007