Klausur mit Lösung 2015

MW-E Mathematikwettbewerb der Einführungsphase
11. Februar 2015
MW-E
Mathematikwettbewerb der Einführungsphase
Hinweis: Von jeder Schülerin bzw. jedem Schüler werden fünf Aufgaben gewertet. Werden mehr als fünf
Aufgaben bearbeitet, so werden nur die mit den höchsten Punktzahlen berücksichtigt.
Der Lösungsweg muss jeweils klar erkennbar sein.
Zugelassene Hilfsmittel sind Taschenrechner, Formelsammlung und Zeichengeräte.
y
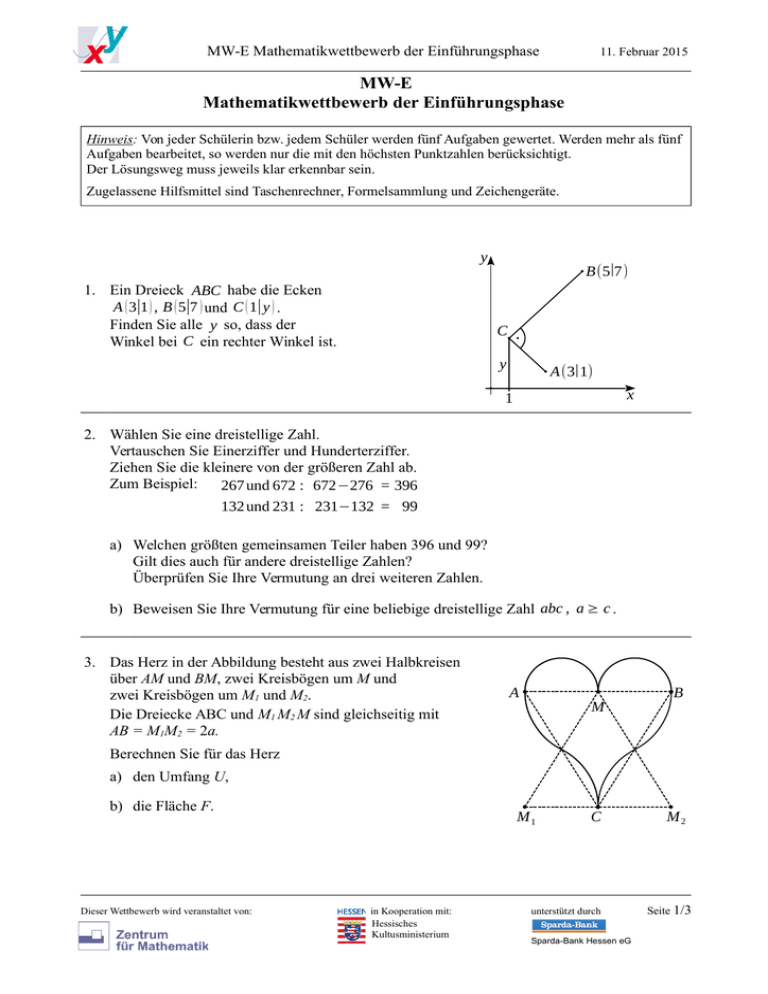
1. Ein Dreieck ABC habe die Ecken
A ( 3|1 ) , B ( 5|7 ) und C ( 1| y ) .
Finden Sie alle y so, dass der
Winkel bei C ein rechter Winkel ist.
B(5|7)
C
y
A(3|1)
x
1
2. Wählen Sie eine dreistellige Zahl.
Vertauschen Sie Einerziffer und Hunderterziffer.
Ziehen Sie die kleinere von der größeren Zahl ab.
Zum Beispiel:
267 und 672 : 672−276 = 396
132 und 231 : 231−132 = 99
a) Welchen größten gemeinsamen Teiler haben 396 und 99?
Gilt dies auch für andere dreistellige Zahlen?
Überprüfen Sie Ihre Vermutung an drei weiteren Zahlen.
b) Beweisen Sie Ihre Vermutung für eine beliebige dreistellige Zahl abc , a ≥ c .
3. Das Herz in der Abbildung besteht aus zwei Halbkreisen
über AM und BM, zwei Kreisbögen um M und
zwei Kreisbögen um M1 und M2.
Die Dreiecke ABC und M1 M2 M sind gleichseitig mit
AB = M1M2 = 2a.
A
M
B
Berechnen Sie für das Herz
a) den Umfang U,
b) die Fläche F.
Dieser Wettbewerb wird veranstaltet von:
M1
in Kooperation mit:
Hessisches
Kultusministerium
C
unterstützt durch
Sparda-Bank Hessen eG
M2
Seite 1/3
MW-E Mathematikwettbewerb der Einführungsphase
11. Februar 2015
4. In einem Halbkreis über AB mit Radius 1 liegt ein Rechteck so,
dass zwei Ecken auf AB liegen und die beiden anderen
auf dem Halbkreis.
Wie muss die halbe Rechteckseite x gewählt werden,
damit die Rechteckfläche F(x) möglichst groß wird?
A
F(x)
⏟
x
B
5. Ein Würfel und ein Oktaeder durchdringen sich so, dass die Kantenmitten
zusammenfallen (siehe Abbildung).
a) Der Würfel habe die Kantenlänge a.
Welche Kantenlänge s hat das Oktaeder?
b) Welche Oberfläche O hat das Oktaeder?
c) Welche Oberfläche hat die Vereinigung von Würfel und
Oktaeder, d. h. die Fläche aller sichtbaren Dreiecke?
6. a) Zeichnen Sie im 1. Quadranten die beiden Parabeln y = x 2 und y 2 = 2 x .
Berechnen Sie die Koordinaten des Schnittpunktes P( a|b) .
b) Zeichnen Sie im x,y-Koordinatensystem die Funktion
f ( x) =
für x > 3
{ 1−|20x−5| fürfür 2x ≤< 2x und
≤3
Dieser Wettbewerb wird veranstaltet von:
in Kooperation mit:
Hessisches
Kultusministerium
unterstützt durch
Sparda-Bank Hessen eG
Seite 2/3
MW-E Mathematikwettbewerb der Einführungsphase
7. Die Konstruktion des
Baumdiagramms erfolgt
nach der Regel
1
1
1
2
a
b
2
1
„Eltern“
1
3
a
a+ b
11. Februar 2015
a+ b
b
„Kinder“
1
4
2
3
3
2
4
3
3
5
5
2
2
5
3
1
5
3
3
4
4
1
Jeder Bruch hat zwei Kinder. Das linke Kind ist ein Bruch kleiner 1, das rechte größer 1.
5
3
2
Zum Beispiel haben die Kinder und die Eltern .
2
2
5
a) Berechnen Sie die 16 Brüche in der nächsten Reihe.
b) Welche Kinder hat
1
?
5
c) Welche Eltern hat
7
?
13
7
d) Welches sind die Großeltern von 13 ?
Das abgebildete Mobile ist nicht im Gleichgewicht,
8. da Kreis, Quadrat und Dreieck unterschiedliche
Gewichte sind.
Aus
+
<
<
<
(links),
(rechts) und
+
(insgesamt)
folgt
<
<
.
Welche Ungleichung für die unterschiedlich
geformten Gewichte folgt aus dem
abgebildeten Mobile?
Dieser Wettbewerb wird veranstaltet von:
in Kooperation mit:
Hessisches
Kultusministerium
unterstützt durch
Sparda-Bank Hessen eG
Seite 3/3
MW- E Mathematikwettbewerb der Einführungsphase
Lösungen
Lösungen zum
Mathematikwettbewerb der Einführungsphase 2015
1. 1. Lösung:
Die Steigungen von AC und BC sind −
Wegen AC ⊥ BC gilt −
y −1
7− y
bzw.
.
2
4
y −1 7− y
⋅
= −1.
2
4
Aus ( y−1)(7− y ) = 8 folgt y 2−8 y +15 = 0 und somit
2
0 = y −8 y +15 = ( y−3)( y −5) ,
also y = 3 oder y = 5.
12P.
2. Lösung:
2
2
2
Es gilt AB = (5−3) +(7−1) = 40 und
2
2
2
2
2
2
2
2
AB = AC + BC = 2 +( y −1) +4 +(7− y ) = 2 y −16 y +70 .
2
Aus 2 y 2−16 y +70 = 40 folgt 0 = y −8 y +15 = ( y−3)( y −5)
und somit y = 3 oder y = 5.
2. a)
981 - 189 = 792 = 8⋅99
693 - 396 = 297 = 3⋅99
801 - 108 = 693 = 7⋅99
6P.
Vermutung: Die Differenz ist immer durch 99 teilbar.
b) abc−cba = 100 a+10 b+ c−(100 c +10 b+a) = 99⋅( a−c).
3. a)
π⋅2 a 7
U = π a+ 4⋅
= πa
6
3
b)
a 2 ( 2 a)
F= π
+
⋅√3 = a2
2
4
()
2
Dieser Wettbewerb wird veranstaltet von:
6P.
6P.
π
6P.
( √3+ 4 )
in Kooperation mit:
Hessisches
Kultusministerium
unterstützt durch
Sparda-Bank Hessen eG
Seite 1/3
MW- E Mathematikwettbewerb der Einführungsphase
Lösungen
4. 1. Lösung:
√
1
1 2
− x 2− .
4
2
1
F ( x) wird maximal für x =
.
2
F (x) = 2 x √ 1−x 2 = 2
(
)
√
12P.
2. Lösung:
F ( x) = 2 x √ 1−x 2 = 2 √ x 2−x 4.
2
2 x (1−2 x )
'
= 0 folgt x = 1 .
Aus F ( x ) =
2
4
2
√ x −x
√
√
1
Da F (0) = F (1) = 0 und F ( x) > 0 für 0 < x < 1, ist x =
ein Maximum.
2
5. a)
4P.
Die Kantenlänge des Oktaeders ist s = a √ 2.
b) Die Oberfläche besteht aus 8 gleichseitigen Dreiecken mit der Seitenlänge s.
s2
Also ist O = 8⋅ √ 3 = 4 a2 √ 3.
4
c)
Die Oberfläche besteht aus 6⋅4 gleichseitigen Dreiecken mit Seitenlänge
und 8⋅3 gleichschenklig rechtwinkligen Dreiecken mit Kathetenlänge
(
a
(
√ 2)
Also ist die gesamte Oberfläche 24⋅
6. a)
4
2
√3+
a
.
2
4P.
a
√2
4P.
( ) )= 3 a ( √ 3+1).
1 a
2 2
2
2
y
Aus b 2 = 2 a und b = a2
folgt a 3 = 2 und b3 = 4,
also P ( √3 2|√3 4 ) .
2
1
Die gesuchte Kantenlänge ist √3 2.
6P.
P(a|b )
1
2
x
f ( x)
b) Für 2 < x ≤ 2,5 ist f ( x) = 1+ (2 x−5) = 2 x−4 .
Für 2,5 < x < 3 ist f ( x) = 1−(2 x −5) = −2 x+6 .
6P.
1
1
Dieser Wettbewerb wird veranstaltet von:
in Kooperation mit:
Hessisches
Kultusministerium
2
3
4
unterstützt durch
Sparda-Bank Hessen eG
x
Seite 2/3
MW- E Mathematikwettbewerb der Einführungsphase
7.
1
4
a)
1
5
8.
4
3
5
4
b)
1
6
und
6
5
c)
Aus
d)
Aus
4
7
5
2
3
5
7
3
3
8
8
5
5
7
2
5
7
2
2
7
5
3
7
5
5
8
Lösungen
3
4
8
3
3
7
4
1
7
4
4
5
3P.
5
1
3P.
7
a
a 7
folgen die Eltern = .
=
13 a+b
b 6
3P.
7 a+ b
a 1
folgen die Eltern = .
=
6
b
b 6
7
1
Also hat
die Großeltern .
13
6
Aus
< 3
+
+
<
+
Aus 4
+
+
< 3
<
Also
<
< 2
(links) folgt
Aus 2
folgt
3P.
(rechts) folgt
+2
+
2
<
12P.
(insgesamt)
<
Dieser Wettbewerb wird veranstaltet von:
in Kooperation mit:
Hessisches
Kultusministerium
unterstützt durch
Sparda-Bank Hessen eG
Seite 3/3