1.3. Beträge, Gleichungen und Ungleichungen

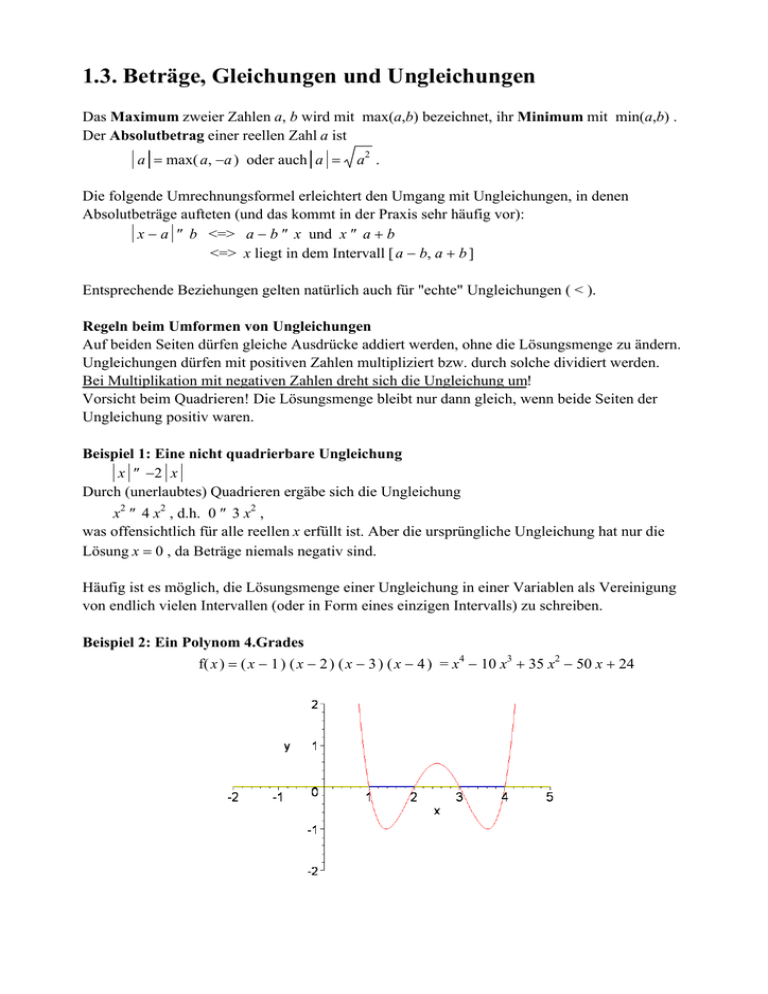
1.3. Beträge, Gleichungen und Ungleichungen
Das Maximum zweier Zahlen a, b wird mit max(a,b) bezeichnet, ihr Minimum mit min(a,b) .
Der Absolutbetrag einer reellen Zahl a ist
a = max( a, −a ) oder auch a =
a2 .
Die folgende Umrechnungsformel erleichtert den Umgang mit Ungleichungen, in denen
Absolutbeträge aufteten (und das kommt in der Praxis sehr häufig vor):
x − a ≤ b <=> a − b ≤ x und x ≤ a + b
<=> x liegt in dem Intervall [ a − b, a + b ]
Entsprechende Beziehungen gelten natürlich auch für "echte" Ungleichungen ( < ).
Regeln beim Umformen von Ungleichungen
Auf beiden Seiten dürfen gleiche Ausdrücke addiert werden, ohne die Lösungsmenge zu ändern.
Ungleichungen dürfen mit positiven Zahlen multipliziert bzw. durch solche dividiert werden.
Bei Multiplikation mit negativen Zahlen dreht sich die Ungleichung um!
Vorsicht beim Quadrieren! Die Lösungsmenge bleibt nur dann gleich, wenn beide Seiten der
Ungleichung positiv waren.
Beispiel 1: Eine nicht quadrierbare Ungleichung
x ≤ −2 x
Durch (unerlaubtes) Quadrieren ergäbe sich die Ungleichung
x2 ≤ 4 x2 , d.h. 0 ≤ 3 x2 ,
was offensichtlich für alle reellen x erfüllt ist. Aber die ursprüngliche Ungleichung hat nur die
Lösung x = 0 , da Beträge niemals negativ sind.
Häufig ist es möglich, die Lösungsmenge einer Ungleichung in einer Variablen als Vereinigung
von endlich vielen Intervallen (oder in Form eines einzigen Intervalls) zu schreiben.
Beispiel 2: Ein Polynom 4.Grades
f( x ) = ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) = x4 − 10 x3 + 35 x2 − 50 x + 24
Die Lösungsmenge der Ungleichung f( x ) ≤ 0 ist die Vereinigung der Intervalle [1,2] und [3,4]
(blau);
denn im Intervall [1,2] ist x − 1 positiv und jeder der drei anderen Faktoren x − 2, x − 3 und x − 4
negativ, während im Intervall [3,4] die ersten drei Faktoren positiv und nur der letzte negativ ist.
Die Lösungsmenge der Ungleichung f( x ) > 0 ist die Komplementärmenge, also die Vereinigung
der Intervalle ]−∞,1[ , ]2,3[ und ]4,∞[ (gelb).
(Achtung: Das Gegenteil von f( x ) > 0 ist nicht f( x ) < 0 , sondern f( x ) ≤ 0.)
Lösungsmengen mehrerer Gleichungen:
Ist A die Menge der Lösungen einer Gleichung f = 0
und B die Menge der Lösungen einer Gleichung g = 0,
so ist die Vereinigung von A und B die Lösungsmenge der Gleichung f g = 0
und der Durchschnitt von A und B die Lösungsmenge der Gleichung f2 + g2 = 0.
Beispiel 3: Vereinigung und Schnitt zweier Kreise
Die allgemeine Koordinatendarstellung zweier Kreise lautet:
( x − a )2 + ( y − b )2 = r2
(Mittelpunkt (a,b), Radius r)
(x − c) + (y − d) = s
(Mittelpunkt (c,d), Radius s)
2
2
2
Durch Subtraktion der zweiten Gleichung von der ersten erhält man die Gleichung der Polaren,
der Geraden durch die beiden Schnittpunkte:
2 ( c − a ) x + 2 ( d − b ) y = r2 − a2 − b2 − s2 + c2 + d2
Auflösen nach x oder y und anschließendes Einsetzen in eine der Kreisgleichungen liefert die
Koordinaten der Schnittpunkte.
Spezialfall: a = 0, b = 0, r = 1, c = 1, d = 1, s = 1.
x2 + y2 = 1
( x − 1 )2 + ( y − 1 )2 = 1
Gleichung der Polaren:
x+y=1
Schnittpunkte:
(1,0) und (0,1).
Die Lösungsmenge der Gleichung
( x2 + y2 − 1 ) ( ( x − 1 )2 + ( y − 1 )2 − 1 ) = 0
ist die Vereinigung der beiden Kreise, während die Lösungsmenge der Gleichung
2
2
( x2 + y2 − 1 ) + ( ( x − 1 )2 + ( y − 1 )2 − 1 ) = 0
nur die beiden Punkte (1,0) und (0,1) enthält.
Durch die Ungleichungen
( x − a )2 + ( y − b )2 ≤ r2
( x − c )2 + ( y − d )2 ≤ s2
werden die gesamten Kreisscheiben (Inneres samt Rand) beschrieben,
während die echten Ungleichungen
( x − a )2 + ( y − b )2 < r2
( x − c )2 + ( y − d )2 < s2
nur das jeweilige Innere der Kreisscheiben (ohne Rand) beschreiben.
Vereinigung:
Durchschnitt:
In den folgenden Beispielen macht man sich zunutze, dass Flächen, die durch Ungleichungen
beschrieben werden, in denen nur die Beträge der Koordinaten x und y vorkommen, symmetrisch
zu beiden Koordinatenachsen sind. Man braucht die Figur also nur in einem Quadranten zu
kennen, die anderen drei Teile entstehen durch Spiegelung an den Achsen.
Beispiel 4: Das Rote Kreuz
Wir beschreiben es durch die Ungleichungen
( x ≤ 1 und y ≤ 3) oder ( x ≤ 3 und y ≤ 1)
Beispiel 5: Rauten
Am einfachsten beschreibt man eine Raute der Breite 2a und der Höhe 2b mit Hilfe der
Ungleichung
x
y
+
≤1.
a
b
Aufgelöst nach y:

x 

x 
 ≤ y und y ≤ b  1 −

b  −1 +

a 

a 
a = 1, b = 1
a = 1, b = 2
a = 1.5, b = 1
Beispiel 6: Ein Weihnachtsstern
( x ≤ 1 und y − x ≤ 1) oder ( y ≤ 1 und x − y ≤ 1)
Die zweite der vier Ungleichungen aufgelöst nach y :
−1 − x ≤ y und y ≤ x + 1
Damit sieht die "erste Hälfte" der Lösungsmenge folgendermaßen aus:
Die "zweite Hälfte" ensteht offenbar durch Vertauschen von x und y . Die zweidimensionale
Darstellung dieser Fläche ist mit Maple etwas kompliziert. Deshalb benutzen wir das 3D-Paket,
mit dem sich das Bild sehr einfach erstellen und außerdem noch im Raum drehen läßt.
Beispiel 7: Das Andreaskreuz
x − y ≤ 1 und x + y ≤ 3
Auflösen des äußeren Absolutbetrages in der ersten Gleichung liefert
y − x ≤ 1 und x − y ≤ 1, also
− x − 1 ≤ y und y ≤ x + 1
sowie die Alternative
y ≤ 1 − x oder (!) x − 1 ≤ y .
Die zweite Ungleichung ergibt die zusätzlichen Bedingungen
x − 3 ≤ y und y ≤ 3 − x .
Damit können wir zwei (sich überlappende) Teile des Andreaskreuzes wie folgt beschreiben:
max( − x − 1, x − 3 ) ≤ y und y ≤ min( x + 1, 3 − x , 1 − x )
max( − x − 1, x − 3, x − 1 ) ≤ y und y ≤ min( x + 1, 3 − x )
Und das gesamte Andreaskreuz sieht dann so aus:
Beispiel 8: BMW
Als nächstes zeichnen wir die Lösungsmenge des Ungleichungssystems
x2 + y2 ≤ 1 , x y < 0 .
Die zweite Bedingung bedeutet, dass entweder x positiv und y negativ ist, oder umgekehrt.
Soviel zu den Bayerischen Motorenwerken. Gehen wir zur Konkurrenz und betrachten
abschließend
Beispiel 9: Der Mercedes-Stern
Die drei Spitzen dieses dreizackigen Sterns um den Mittelpunkt m = ( 0, 0 ) lassen sich wie folgt
beschreiben:
 7π
 7 π 
  11 π 
 11 π  
, sin
  , a3 =  cos
, sin
 
a1 = ( 0, 1 ) , a2 =  cos
  6 
 6 
  6 
 6 
Hinzu kommen die drei "inneren" Ecken (mit Abstand r vom Mittelpunkt):

π
 π 

5π
 5 π 
, r sin
  .
i1 = ( 0, −r ) , i2 =  r cos , r sin   , i3 =  r cos

6
 6 

 6 
 6 
Wir verbinden je drei dieser Punkte mit dem Mittelpunkt, ergänzen sie durch zwei Seiten zu je
einem (nicht konvexen) Viereck und setzen diese Vierecke zusammen. Schließlich bauen wir
außen herum noch einen Ring.