Übung zu Strahlensätzen 2 Abbildung 1: Die Strahlensätze 1. Die

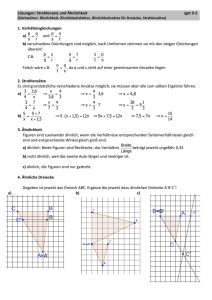
Übung zu Strahlensätzen 2
Abbildung 1: Die Strahlensätze
1. Die Anwendung der Strahlensätze kann etwas komplizierter werden, wenn man
mit Hilfe der parallelen Strecken (in der Abbildung 1 sind dies e und f ) Strecken
auf den Strahlen bestimmen will. Nehmen wir als Beispiel e = 5 cm, f = 10 cm und
d = 8 cm. Gesucht wird damit c. Wir stellen den Strahlensatz auf:
c
=
c+8
5
10
Die Variable c, nach der wir suchen, kommt zwei Mal in der Gleichung vor. Wie
gehen wir vor? In den ersten Schritten ist es klug, die Brüche zu beseitigen:
c
c+8
⇐⇒ 10 ∗
5
| ∗ 10
10
=
c
c+8
5| ∗ (c + 8)
=
⇐⇒ 10c
= 5 ∗ (c + 8)
⇐⇒ 10c
=
5c + 40
Nun sortieren wir die beiden Seiten der Gleichung: die Variablen kommen auf
eine Seite der Gleichung, die Zahlen auf die andere Seite und zum Schluss dividieren, so dass die Variable alleine steht:
⇐⇒ 10c = 5c + 40| − 5c
⇐⇒ 5c
=
⇐⇒ c
=
40| : 5
8
Bestimmen Sie die fehlenden Teile in der Tabelle. Die Bezeichnungen beziehen
sich auf die Abbildung 1.
Aufgabe
a)
b)
c)
d)
a
6 cm
b
10 cm
c
4 cm
6 cm
7 cm
5 cm
© Michael Dröttboom
1
2. Lösen Sie die folgenden Aufgaben:
d
8 cm
10 cm
e
8 cm
9 cm
10 cm
24 cm
f
10 cm
12 cm
12 cm
8 cm
LernWerkstatt-Selm.de
Übung zu Strahlensätzen 2
Abbildung 2: Aufgaben zu Strahlensätzen
© Michael Dröttboom
2
LernWerkstatt-Selm.de
Übung zu Strahlensätzen 2
1. Es gilt
Aufgabe
a)
b)
c)
d)
a
6 cm
30 cm
7 cm
2,5 cm
b
1,5 cm
10 cm
1,4 cm
5 cm
c
4 cm
6 cm
40 cm
5 cm
d
1 cm
2 cm
8 cm
10 cm
e
8 cm
9 cm
10 cm
24 cm
f
10 cm
12 cm
12 cm
8 cm
2. Aufgabe 5a) Der Baum ist ungefähr 22 Meter hoch, siehe b)
Aufgabe 5b) Bei einem Winkel von 45° ist das Dreieck ein gleichschenkliges (der
Winkel oben rechts in der Ecke ist auch 45°, somit sind auch die beiden Seiten
gegenüber diesen Winkeln gleich groß) . Somit sind auch in dem großen Dreieck,
das den Baum enthält, die Entfernung zum Baum und die Höhe des Baums gleich.
Dazu muss noch 1 Meter addiert werden (Blickhöhe)
←−−
Aufgabe 6) Es gilt AD = AB + BD. Nach dem ersten Strahlensatz ist vorne zu
hinten wie vorne zu hinten:
⇐⇒
AB
BD
AB
10
AC
CE
63
=
| ∗ 10
14
63
= 10 ∗
14
=
45
=
⇐⇒ AB
⇐⇒ AB
Die Seite AD ist damit 55 Meter lang.
Aufgabe 7) Nach dem zweiten Strahlensatz (die Parallelen werden genutzt, wir
müssen vom Zentrum P ausgehen) gilt
x
x+a
x
⇐⇒
x + 20
⇐⇒ 28x
d
b
20
=
| ∗ (x + 20)| ∗ 28
28
= 20 ∗ (x + 20)
=
⇐⇒ 28x
=
⇐⇒ 8x
=
⇐⇒ x
=
20x + 400| − 20x
400| : 8
50
Aufgabe 8) Nach dem zweiten Strahlensatz gilt - ähnlich wie in Aufgabe 7 -
© Michael Dröttboom
3
LernWerkstatt-Selm.de
Übung zu Strahlensätzen 2
⇐⇒
AB
EF
AB
66
=
=
⇐⇒ AB
=
⇐⇒ AB
=
P E + EA
EA
154
| ∗ 66
96
154
∗ 66
96
105, 875
Aufgabe 9) Auch hier wird der 2. Strahlensatz verwendet, da wir mit den Parallelen arbeiten:
CT
CT + RC
CT
⇐⇒
CT + 40
⇐⇒ 36 ∗ CT
CD
RS
24
=
| ∗ 36| ∗ (CT + 40)
36
= 24 ∗ (CT + 40)
⇐⇒ 36 ∗ CT
=
⇐⇒ 12 ∗ CT
=
⇐⇒ CT
=
=
24 ∗ CT + 960| − 24 ∗ CT
960| : 12
80
Damit ist die gesuchte Länge 120 Meter.
© Michael Dröttboom
4
LernWerkstatt-Selm.de