11-L5-vor-Matrizen-I..

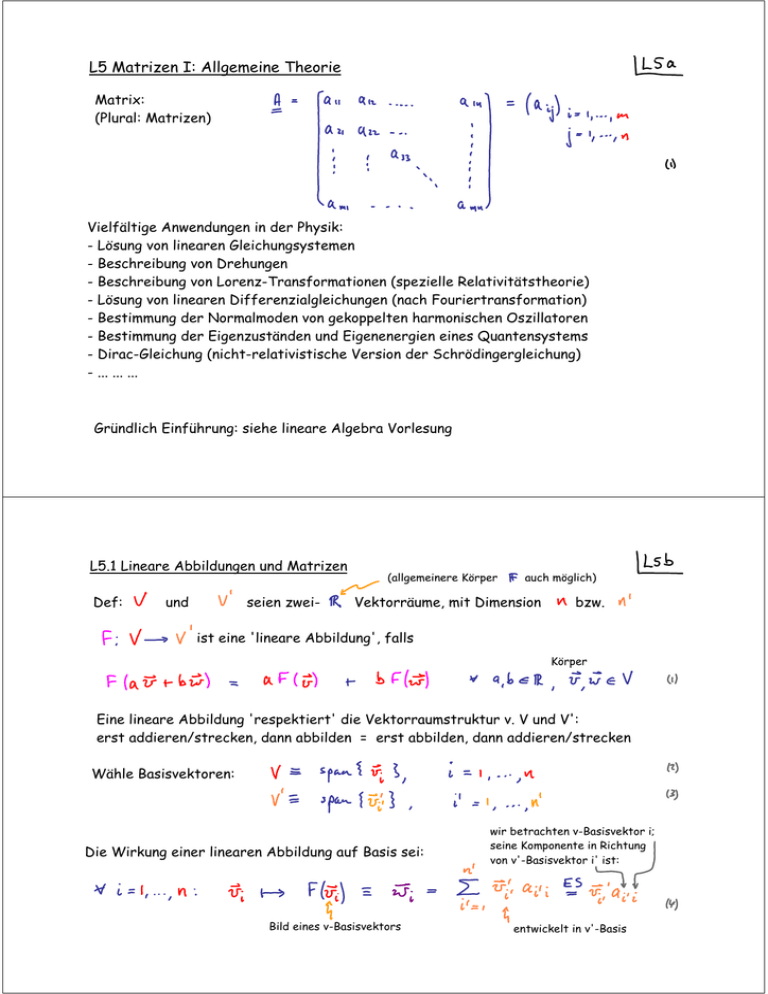
L5 Matrizen I: Allgemeine Theorie
Matrix:
(Plural: Matrizen)
Vielfältige Anwendungen in der Physik:
- Lösung von linearen Gleichungsystemen
- Beschreibung von Drehungen
- Beschreibung von Lorenz-Transformationen (spezielle Relativitätstheorie)
- Lösung von linearen Differenzialgleichungen (nach Fouriertransformation)
- Bestimmung der Normalmoden von gekoppelten harmonischen Oszillatoren
- Bestimmung der Eigenzuständen und Eigenenergien eines Quantensystems
- Dirac-Gleichung (nicht-relativistische Version der Schrödingergleichung)
- ... ... ...
Gründlich Einführung: siehe lineare Algebra Vorlesung
L5.1 Lineare Abbildungen und Matrizen
Def:
und
seien zwei-
(allgemeinere Körper
auch möglich)
Vektorräume, mit Dimension
bzw.
ist eine 'lineare Abbildung', falls
Körper
Eine lineare Abbildung 'respektiert' die Vektorraumstruktur v. V und V':
erst addieren/strecken, dann abbilden = erst abbilden, dann addieren/strecken
Wähle Basisvektoren:
Die Wirkung einer linearen Abbildung auf Basis sei:
Bild eines v-Basisvektors
wir betrachten v-Basisvektor i;
seine Komponente in Richtung
von v'-Basisvektor i' ist:
entwickelt in v'-Basis
Beispiel:
Laut
Skizze:
Können wir hieraus die Wirkung v. F auf einen anderen Vektor,
Wir werden zeigen, dass allgemein gilt:
bestimmen? Ja!
mit
Allgemein:
F ist linear:
Wirkung v. F auf
v-Basisvektoren ist
bekannt:
Umstellung der
Doppelsumme:
Kurzversion
mittels ES:
Koeffizient bezüglich v'Basis
(u. Klammern weglassen)
Fazit: Lineare Abbildung ist vollständig durch die Koeffizienten
(es gibt
von ihnen) festgelegt, die die Wirkung v. F auf Basisvektoren beschreiben!
Dasselbe ausgedrückt durch die Koordinatenvektoren:
(siehe L2.4a.3)
implizit:
(2) bedeutet
mehr explizit:
Definition v. neuer Art v. 'Multiplikation:
Matrix mal Vektor'
Def: Matrix (Plural: Matrizen)
'm x n Matrix'
ist rechteckiges Zahlenschema mit m Zeilen und n Spalten,
und 'Matrixelementen'
n Spalten
m x n Matrix:
m Zeilen
'Quadratische Matrix'
falls
Notationskonventionen für Matrizen:
Menge der reellen m x n Matrizen:
Matrixelemente
Multiplikation: Matrix mal Spaltenvektor
Spaltenvektor mit n Komponenten
ist nx1 Matrix.
per Definition
Beispiele:
[vergleiche (c.4)]
Einschub: Matrizen bilden einen Vektorraum
ist Vektorraum, mit folgenden Def. für Addition, Skalarmult.:
(i) Matrixaddition:
(elementenweise Addition)
Explizit:
(m = n = 2)
Beispiel:
Neutrales Element der Matrixaddition: "Nullmatrix" :
(bestehend aus lauter Nulleinträgen)
Negatives Element ( = inverses Element der Addition):
Lösung
Matrix bestehend aus den negativen Matrixelementen
Matrixaddition ist assoziativ:
und kommutativ:
(ii) Skalarmultiplikation:
(elementenweise Multiplikation)
Explizit:
(m = n = 2)
Beispiel:
mit Matrixaddition und skalarer Multiplikation gestattet, ist ein
-dimensionaler (reeller) Vektorraum [äquivalent zu
]
Lineare Abbildungen zwischen Standardvektorräumen
Sei
mit Standardbasis
und
mit Standardbasis
dann liefert (b.4):
Bild eines Standard-Basisvektors
entwickelt in Standard-Basis
Position i:
Spalte i der Matrix
Fazit: lineare Abbildung
Spalte i der Matrix
wird dargestellt durch
, ist Bild des Basisvektors
unter Abbildung F.
Matrixmultiplikation
(entspricht d. Verknüpfung v. zwei
linearen Abbildungen)
implizit:
implizit:
Kompaktfassung: Verknüpfung v. B mit A liefert:
Fazit: Koeffizienten der Matrix
C sind gegeben durch:
Kurznotation für (3):
(3) ist die definierende Gleichung für 'Matrix-Multiplikation' !
Matrixmultiplikation:
(zusätzliche Struktur zu der des Vektorraums)
Skalarprodukt von "i-tem Zeilenvektor v. B" und "k-tem Spaltenvektor v. A"
Nur definiert falls (# Zeilen v. B) = (# Spalten v. A).
Explizit:
n Zeilen und k Spalten:
n Zeilen und m Spalten:
i-ter Zeilenvektor v. B
Beispiel:
m Zeilen und l Spalten:
k-ter Spaltenvektor v. A
m = 3, n = 2, p = 2
Eigenschaften der Matrixmultiplikation:
1) nicht kommutativ:
(sogar gar nicht definiert,
falls Dimensionen nicht passen!)
Beispiel: (für m = n = p = 2)
verschieden !
verschieden !
2) assoziativ
(falls definiert)
Beweis:
denn skalare Addition
ist assoziativ
Beispiel: (m = n = p = 2)
Assoziativität gnadenlos explizit, für m = n = p = 2:
genau die gleichen Terme kommen vor (nur in unterschiedlicher Reihenfolge)
3. distributiv
Beweis:
ebenso:
4.
Beweis:
5. Falls
Quadratische Matrizen sind "abgeschlossen" unter Matrixmultiplikation.
"Einheitsmatrix (engl: identity)":
(für m = n)
(Einser auf der Diagonalen, Nullen sonst)
6. Neutrales Element der Matrixmultiplikation:
denn:
Explizit:
(n=3)
Quadratische Matrizen bilden eine "Algebra", das ist ein Vektorraum mit
zusätzlicher Multiplikation mit Verträglichkeitsbedingungen (assoziativ, distributiv),
und Einselement.