Kurzreferat „Einfache Maschinenmodelle“ Seite 1/9 Arne M

Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Seite 1/9
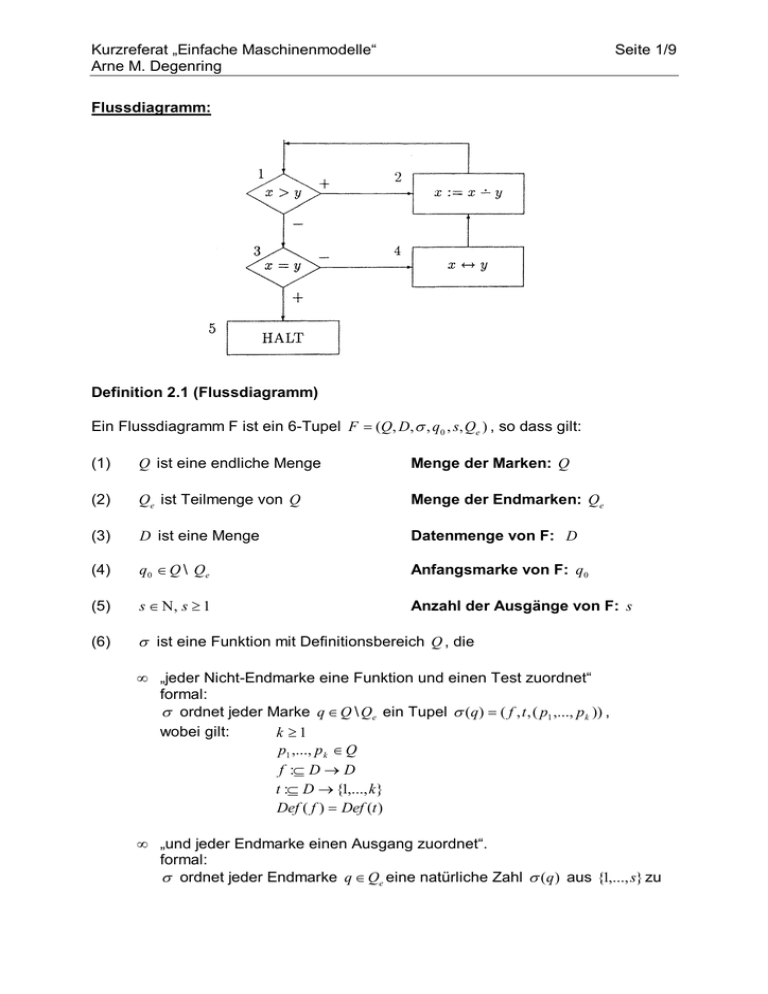
Flussdiagramm:
Definition 2.1 (Flussdiagramm)
Ein Flussdiagramm F ist ein 6-Tupel F = (Q, D, σ , q0 , s, Qe ) , so dass gilt:
(1)
Q ist eine endliche Menge
Menge der Marken: Q
(2)
Qe ist Teilmenge von Q
Menge der Endmarken: Qe
(3)
D ist eine Menge
Datenmenge von F: D
(4)
q0 ∈ Q \ Qe
Anfangsmarke von F: q0
(5)
s ∈ Ν, s ≥ 1
Anzahl der Ausgänge von F: s
(6)
σ ist eine Funktion mit Definitionsbereich Q , die
•
„jeder Nicht-Endmarke eine Funktion und einen Test zuordnet“
formal:
σ ordnet jeder Marke q ∈ Q \ Qe ein Tupel σ (q) = ( f , t , ( p1 ,..., p k )) ,
wobei gilt:
k ≥1
p1 ,..., p k ∈ Q
f :⊆ D → D
t :⊆ D → {1,..., k}
Def ( f ) = Def (t )
•
„und jeder Endmarke einen Ausgang zuordnet“.
formal:
σ ordnet jeder Endmarke q ∈ Qe eine natürliche Zahl σ (q ) aus {1,..., s} zu
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Definition 2.2 (Semantik eines Flussdiagramms)
Seite 2/9
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Seite 3/9
Maschine
M = ( F , X , Y , EC , AC )
Maschine:
Flussdiagramm F (mit Datenmenge D )
mit
Eingabemenge X und Eingabecodierung EC : X → D
und Ausgabemenge Y sowie Ausgabecodierung AC : D → Y
Semantik von M:
( f M , tM )
F habe s Ausgänge.
Von M berechnete Funktion:
Von M berechneter Test:
f M :⊆ X → Y definiert durch f M := AC o f F o EC
t M :⊆ X → {1,...s} definiert durch t M := t F o EC
Registermaschine
Datenmenge:
d (0) d (1) d (2) ...
R0
Operationen:
R1
R2
Ri := Ri + 1
Ri := Ri − 1
Ri = 0
Definition 3.1 (Registermaschine)
...
Addiere 1
Subtrahiere 1
Teste ob 0
(arithmetische Differenz!)
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Definition 3.2 (Berechenbare Zahlenfunktion)
„Register-berechenbar“:
Beweisverfahren für Behauptung: „ f :⊆ Ν k → Ν ist berechenbar “:
•
•
Flussdiagramm einer Registermaschine angeben
Beweisen, dass für zugehörige Maschine f = f M
(Entsprechendes gilt für Tests.)
Definition 3.3 (verallgemeinerte Registermaschine)
Es werden
Befehle der Art
und zweiwertige Tests der Art
Rn := g ( Ri1 ,..., Rim )
t ( Ri1 ,..., Rim )
zugelassen für beliebige g und t (sogar partielle).
Formale Definition:
Seite 4/9
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Seite 5/9
Berechenbarkeitsnachweise können nun wie folgt geführt werden:
•
Konstruktion einer verallgemeinerten Registermaschine M, und Beweis,
dass M die gesuchte Funktion bzw. Test berechnet
•
Nachweis, dass jede im Flussdiagramm von M verwendete Funktion
berechenbar ist
Dadurch gelingt der Nachweis der Berechenbarkeit vieler bekannter Funktionen, z.B.
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Seite 6/9
Verfeinerung / Einsetzung
Satz 4.1 (Umbenennung von Marken)
Marken können beliebig umbenannt werden, ohne dass sich die Semantik verändert
=> Marken müssen bei grafischen Darstellungen nicht angegeben werden
Einsetzung / Verfeinerung
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Seite 7/9
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Seite 8/9
Satz 4.3 (Verfeinerung)
Semantik ändert sich nicht, wenn ein Befehl ersetzt wird durch ein Flussdiagramm
gleicher Semantik.
Simulation:
Datenmengen können durch andere Darstellung simuliert werden.
Z.B. Natürliche Zahlen als String speichern
Kurzreferat „Einfache Maschinenmodelle“
Arne M. Degenring
Lemma 4.6 (Simulation von Maschinen)
Zusätzlich Eingabeanpassung und Ausgabeanpassung
Seite 9/9