ir v xY - Physik in Jena
Werbung

TuBonprlscHE MpcHarutN
(Sommersemester 2010)
Thema 4: Bewegung im Zentralkraftfeld. Das Kopt pR-Problem
Aufgabe 1; Der Amboß des Hostoo
Dem griecirischen Dichter HBsio» zufolge erreicht ei,n metalli,scher Ambofi, der neun Tage
und Nrichte lang uom Himmel herabftillt, 1...1 di.e Erde am zehnten Tag.
Während wir heute eher meinen, der Hirnmel sei unendlich weit weg, war der Kosmos nach
den damaligen Weitvorstellungen in neun Sphären eingeteilt und damit endlich. Es war
aiso delkbar, daß die Götter die Himmelspforte öffneten und einen Amboß aus großer,
aber endlicher Entfernung auf die Erde fallen ließen.
Es seien .R cler Erdradius und h die über der Erdoberfläche gemessene Höhe. Leiten
Sie aus dem NnwroNschen Gravitationsgesetz das Fallgesetz für den radialen, auf
den Erdmittelpunkt gerichteten freien Fall her. Wie ändert sich die Schwerebeschleu, nigung rnit clei Höhe? Zeigen Sie, daß für h <.R das Galtlctsche Fallgesetz itt: -g
mit g als der schwerebeschleunigung an der Erdoberfläche richtig folgt.
a)
b) Benutzen Sie den Energieerhaltungssatz, um für
den freien Fall aus großer Höhe ä6
Auftreffgeschwindigkeit up und die
die
Anfangsgeschwindigkeit
mit verschwindender
Fallzeii tp bis zur Brdoberfläche zu bestimmen.
Hinweis: Sei X:a,r*b,Y:
fr*S
und
A:bf -
f ,,1lY : sgn(X)
r* A sgn(o)
v xY =i.r
;ä
J Xd,
ag. Dann gilt für a.f
<0
arctan
Dabei bedeutet das Symbol ,,sgn" das Vorzeichen der jeweiligen Größe.
Sie ausgehend von Ihrem Resultat nach, daß sich unter den Gültigkeitsbedingungen des GaltLBlschen Fallgesetzes die Fallzeit auf den bekannten Ausdruck
c) Weisen
17
to:
d)
\12|f,
reduziert.
Gervinnen Sie für h,s ) -R eine Näherungsformel zur Berechnung der Fallzeit
überprüfen Sie damit die Vorstellungen des Hnstoo wie folgt:
tp
uncl
o Da die Griechen aile Planeten bis zum Saturn kannten, ist
'
die Annahme sinnvoll,
der
des
befindet. Berechnen
Himmelspforte.jenseits
Sphäre
Saturn
daß sich die
Sie die Fallzeit des Amboß', wenn er aus dem Abstand des den Griechen nicht
bekannten Planeten tlranus Iällen geiassen und allein von der Erde angezogen
rrird.
o Wie ändert sich die Falizeit bis zur Erde, wenn der Arnboß von cler Sonne
angezogen und die Erdanziehung vernachlässigt wird?
e) Bestätigen Sie für die Auftreffgeschwindigkeit das Galti,Elsche Resultat up : JSia
für hs (( ß. Wetches interessante Ergebnis erhalten Sie für die Ariftreffgeschwindigkeit beim Fa1l ,,aus dern Unendlichen"?
bitte wenden
Aufgabe 2: Die dritte
J<osrnische Geschwindigkeit
Die dritte kosrnische Geschwindiglceit ist die Antwort auf die Frage, welche mi,nimale Geschwindigkeit ein Projektii haben muß, damit es aus dem Abstand Sonne - Erde und von
der Erdoberfläche aus das Sonnensystem verlassen kann.
Berechnen Sie diese Geschwindigkeit in zwei Schritten:
a)
Skizzieren Sie die Überlagerung der NswtoNschen Potentiale von Sonne und Erde und ermittein Sie zunächst - analog zur zweiten kosmischen Geschwindigkeit -'
für dieses Potential die radiale Fluchtgeschwindigkeit von der Erdoberfläche. Außer
Sonne und Erde sollen keine u,eiteren Himmelskörper einbezogen werden.
b) Berücksichtigen Sie nun die Bewegurrg der Erde auf ihrer
als kreisförmig angenomrienen Bahn, iedoch nicht ihre Eigenrotation, und wählen Sie eine günstige Abschußrichtung für das Projektil.
Aufgabe 3: Die Periheldrehulg der Planet,en
Nach der Allgemeinen Relativitälstheorie muß das NnwtoNsche Potential für clie Bervegung del Planeten im Zentralhraftfeld der Sonne um einen Zusatzterm erweitert werden:
(Jb\:
*; - pß
(r) : *1
nrir. a
nrll
o:: GlVlm
GMm und
ur
{J
:3
G2AI2-
,2
Der Zusatzterm ist ein Störterm, denn es gilt mit P als Drehimpulsbetrag
'
.
# U,
a) Überführen
Sie rnit cler Substitution s - | den Energie-Erhaltungssatz für das effektive Potential Li"6 in eine Differentialgleichung vom Typ einer iniromogenen Schwin-
gungsgleichung uncl lösen Sie diese.
b) Während bei cler Bewegung im NpwroNschen Potential der,,entartete" Fall vr-irliegt,
daß der Planet nach Überstreichen des Winkels 2zr wieder zu seinern Ausga,ngspunkt
(Perihel) zurückkehrt, muß er in dem korrigierten Potential einen zusätzlichen Winkel
Arp zurückiegen) um wieder das Perihel zu erreichen. Lesen Sie aus lhrer Lösung diese
Periheldrehung Ag ab und skizzieren Sie die Bahn, die sich - wenn auch wenig * von
einer Ellipse urrtersciieidet
.
c)
Beschreiben Sie die Periheldrehung statt durch den Drehimpuls P clurch große Halbachse o rind Exzentrizität e der ungestörten Bahneilipse. Unter weichen Bedingungen
lassen sich,,große" Perihelverschiebungen erwarten?
d)
Berechnen Sie die Perihelverschiebung für den Merkur uncl geben Sie cliese in Bogensekunden pro Jahrhundert an.
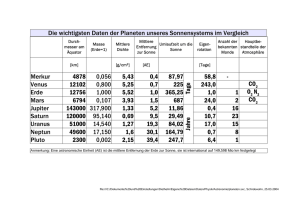
Hinweis für alle Aufgaben:
Entnehmen Sie für numerische Berechnungen die Daten
Tafehverk"
ftir
Sonne und Planeten einem