Abbildungen mit Sammellinsen
Werbung

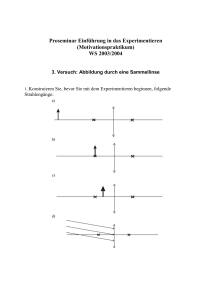
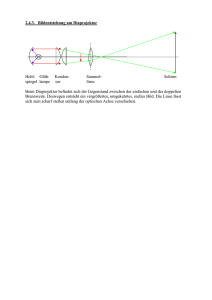
Abbildungen mit Sammellinsen Konstruktion des Bildes einer Sammellinse: Einen Bildpunkt einer Abbildung einer Linse kann man mit einem Lichtstrahl, der parallel zur optischen Achse verläuft, und einem Lichtstrahl, der durch den Mittelpunkt der Linse läuft, konstruieren. Dort wo sich die beiden Strahlen kreuzen, ist der Bildpunkt der Abbildung. Lichtstrahlen, die von einem Gegenstand ausgehen, dessen Gegenstandsweite g größer ist als die Brennweite f der Linse, werden an einer Sammellinse so gebrochen, dass sie sich wieder in einem Punkt scheiden. Von einem Gegenstand der Höhe G, der sich in der Gegenstandsweite g > f vor einer Sammellinse der Brennweite f befindet, entsteht in der Bildweite b ein optisches Bild der B b Höhe B. Dabei beträgt der Abbildungsmaßstab A= = . Außerdem gilt die G g 1 1 1 = . Linsengleichung f g b Dabei beschreibt der Abbildungsmaßstab das Verhältnis von Bildghöhe und Gegenstandshöhe. So ist bei einem Abbildungsmaßstab von drei das Bild drei mal so groß wie der Gegenstand. Ein Gegenstand der Größe 4cm erzeugt bei einem Abbildungsmaßstab von drei also ein 12 cm großes Bild. Die Linsengleichung dagegen beschreibt, wo eine Linse ein scharfes Bild eines Gegenstandes erzeugt. Bei einer Linse mit der Brennweite f = 3 cm entsteht ein Bild eines Gegenstandes, der 10 cm vor der Linse steht (Gegenstandsweite g = 9cm), in einer Entfernung von 4,5cm (Bildweite b=4,5cm). Mittelebene einer Linse G Gegenstandshöhe F optische Achse Mittelpunktstrahl g Gegenstandsweite b Bildweite B Bildhöhe Brennweite f Lichtstrahl parallel zur optischen Achse