Binomialkoeffizient, Binomialverteilung

Binomialkoeffizient, Binomialverteilung
1. Eine Laplace-Münze wird n-mal geworfen, Kopf“ ist ein Treffer, Zahl“ eine Niete.
”
”
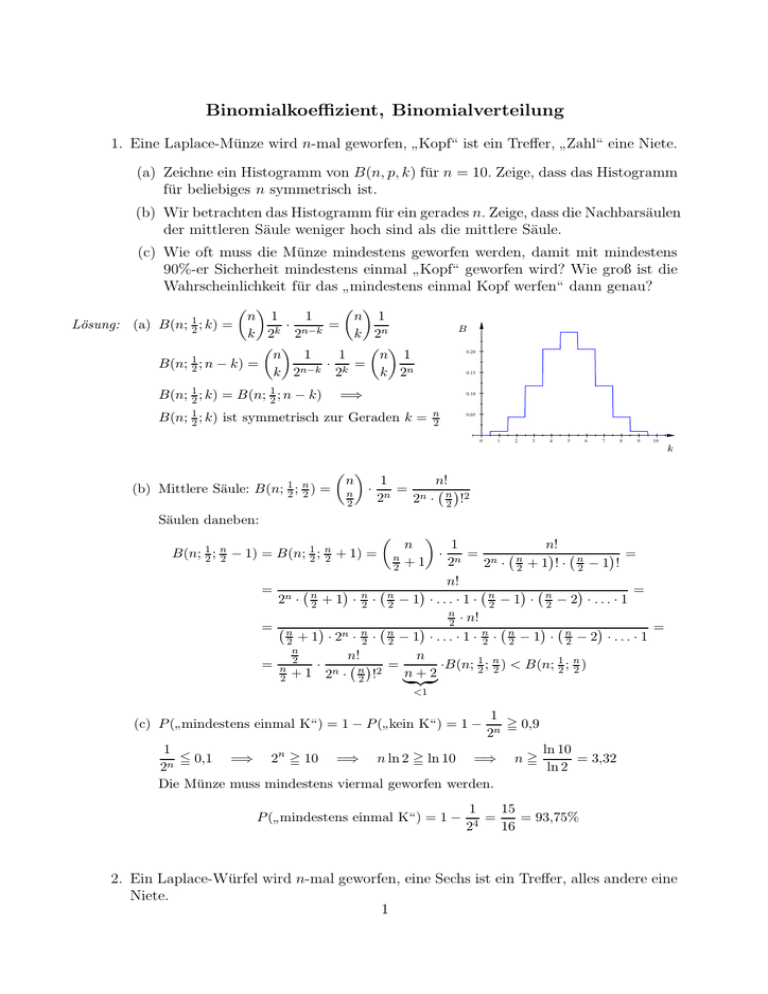
(a) Zeichne ein Histogramm von B(n, p, k) für n = 10. Zeige, dass das Histogramm
für beliebiges n symmetrisch ist.
(b) Wir betrachten das Histogramm für ein gerades n. Zeige, dass die Nachbarsäulen
der mittleren Säule weniger hoch sind als die mittlere Säule.
(c) Wie oft muss die Münze mindestens geworfen werden, damit mit mindestens
90%-er Sicherheit mindestens einmal Kopf“ geworfen wird? Wie groß ist die
”
Wahrscheinlichkeit für das mindestens einmal Kopf werfen“ dann genau?
”
n 1
n 1
1
Lösung: (a) B(n;
=
· n−k =
k
k 2 2
k 2n
n
1
n 1
1
·
=
B(n; 21 ; n − k) =
k 2n−k 2k
k 2n
1
2 ; k)
B(n; 21 ; k) = B(n; 21 ; n − k)
B
0.20
0.15
=⇒
0.10
B(n; 21 ; k) ist symmetrisch zur Geraden k =
n
2
0.05
0
1
2
3
4
5
6
7
8
9
10
k
(b) Mittlere Säule: B(n;
1 n
2; 2 )
=
n
n
2
n!
1
= n n 2
n
2
2 · 2 !
·
Säulen daneben:
B(n;
1 n
2; 2
− 1) = B(n;
=
=
=
2n ·
1 n
2; 2
+ 1) =
+1 ·
n
2
n
2 +1
n
2
·
n
+
1
2
n
2
·
· 2n · n2 ·
n!
n
2 · n2 !2
n
n!
1
=
· n = n n
n
2
+
1
2 · 2 + 1 ! · n2 − 1 !
2
n!
n
=
n
n
2 − 1 · ... · 1 · 2 − 1 · 2 − 2 · ... · 1
n
2 · n!
n
=
n
n
n
2 − 1 · ... · 1 · 2 · 2 − 1 · 2 − 2 · ... · 1
n
·B(n; 21 ; n2 ) < B(n; 12 ; n2 )
=
n
+
2
| {z }
<1
1
(c) P ( mindestens einmal K“) = 1 − P ( kein K“) = 1 − n ≧ 0,9
”
”
2
ln 10
1
= 3,32
≦ 0,1 =⇒ 2n ≧ 10 =⇒ n ln 2 ≧ ln 10 =⇒ n ≧
n
2
ln 2
Die Münze muss mindestens viermal geworfen werden.
1
15
P ( mindestens einmal K“) = 1 − 4 =
= 93,75%
”
2
16
2. Ein Laplace-Würfel wird n-mal geworfen, eine Sechs ist ein Treffer, alles andere eine
Niete.
1
(a) Zeichne ein Histogramm von B(n, p, k) für n = 10.
(b) Wie oft muss der Würfel mindestens geworfen werden, damit mit mindestens
90%-er Sicherheit mindestens ein Treffer erzielt wird? Wie groß ist die Wahrscheinlichkeit für mindestens ein Treffer“ dann genau?
”
Lösung: (a)
k
0
1
2
3
4
5
6
7
8
9
10
B(10, 16 , k)
16,15%
32,30%
29,07%
15,50%
5,43%
1,30%
0,22%
0,025%
1,86 · 10−3 %
8,27 · 10−5 %
1,65 · 10−6 %
B
0.3
0.2
0.1
0
1
2
3
4
5
6
7
8
9
10
k
1
5
(b) p = , q = 1 − p =
6
6
P ( mindestens einmal 6“) = 1 − P ( keine 6“) = 1 − q n ≧ 0,9
”
”
ln 0,1
n
= 12,6
q ≦ 0,1 =⇒ n ≧
ln 56
Der Würfel muss mindestens 13-mal geworfen werden.
13
5
P ( mindestens einmal 6“) = 1 −
= 90,65%
”
6
3. Magdalena hat beim Stehendschießen die Trefferwahrscheinlichkeit p = 80%.
(a) Magdalena schießt zwanzigmal. Wie groß ist die Wahrscheinlichkeit p1 , dass sie
folgende Serie schießt: 10011 11011 10111 01111?
(b) Wie groß ist die Wahrscheinlichkeit p2 , dass sie bei zwanzig Schüssen genau 15
Treffer landet?
(c) Eine Serie besteht aus fünf Schüssen, eine Topserie aus fünf Treffern. Mit welcher Wahrscheinlichkeit pT schießt Lena eine Topserie? Wie viele Serien muss
Magdalena mindestens schießen, damit mit mindestens 95%-iger Wahrscheinlichkeit mindestens eine Topserie dabei ist?
1
415
4
= 0,8, q = 1 − p = = 0,2, p1 = p15 q 5 = 20 = 1,126 · 10−5
5 5
5
20 15 5
20 15 5 15504 · 415
(b) p2 =
p q =
p q =
= 17,46%
15
5
520
| {z }
Lösung: (a) p =
15504
45
1024
= 0,32768 = 32,768%
3125
2101
= 0,67232 = 67,232%
q T = 1 − pT =
3125
2
(c) pT = p5 =
55
=
n
n
P ( kein Treffer“) = qT
, P ( mindestens ein Treffer“) = 1 − qT
”
”
ln 0,05
n
n
= 7,55
1 − qT
≧ 0,95 =⇒ qT
≦ 0,05 =⇒ n ≧
ln qT
Lena muss mindestens acht Serien schießen.
4. An wie vielen Ziehungen muss man beim Lotto 6 aus 49“ mit jeweils einem Tipp
”
mindestens teilnehmen, um mit mindestens 90%-iger Wahrscheinlichkeit mindestens
einmal sechs Richtige zu haben?
Lösung: p =
n≧
1
49
6
=
13983815
1
= 7,151 · 10−8 , q = 1 − p =
= 0,9999999285
13983816
13983816
ln 0,1
= 32 198 925,11, also mindestens 32 198 926-mal.
ln q
5. Beim genetischen Fingerabdruck werden mehrere Abschnitte der DNA vervielfältigt
und auf ihre Länge hin untersucht. Nehmen wir an, dass zehn Abschnitte untersucht
werden und jeder Abschnitt zufällig verteilt fünf verschiedene Längen haben kann
(die Realität ist komplizierter).
(a) An einem Tatort werden DNA-Spuren des Täters gesichert. Wie groß ist die
Wahrscheinlichkeit p, dass der genetische Fingerabdruck einer beliebigen Person mit dem des Täters übereinstimmt?
(b) Wie groß ist die Wahrscheinlichkeit, dass bei 10 000 Verurteilungen auf Grund
des genetischen Fingerabdrucks mindestens ein Unschuldiger dabei ist?
(c) Ab wie vielen Verurteilungen auf Grund des genetischen Fingerabdrucks ist mit
einer mindestens 50%-igen Wahrscheinlichkeit mindestens ein Unschuldiger ins
Gefängnis gewandert?
Lösung: (a) Es gibt z = 510 = 9 765 625 verschiedene Möglichkeiten, also ist
p=
(b) q = 1 − p =
1
= 1,024 · 10−7
9 765 625
9 765 624
765 625 = 0,999 999 8976
9
=⇒
p1 = 1 − q 10000 = 1,0235 · 10−3 = 0,10235%
(c) 1 − q n ≧ 0,5
=⇒
q n ≦ 0,5
=⇒
n≧
ln 0,5
= 6 769 015,09
ln q
6. Aus einem Kartenspiel mit 32 Blatt wird mit Zurücklegen immer eine Karte gezogen.
Ein Treffer (mit 1 bezeichnet) liegt vor, wenn die gezogene Karte ein Ass ist, sonst
eine Niete (mit 0 bezeichnet).
3
(a) Der Versuch wird zehnmal ausgeführt. Mit welcher Wahrscheinlichkeit tritt das
Ergebnis 0001001001 ein?
(b) Mit welcher Wahrscheinlichkeit sind beim zehnmaligen Kartenziehen genau
drei Treffer dabei?
(c) Mit welcher Wahrscheinlichkeit ist beim zehnmaligen Kartenziehen mindestens
ein Treffer dabei?
(d) Mit welcher Wahrscheinlichkeit sind beim zehnmaligen Kartenziehen mindestens drei Treffer dabei?
(e) Wie viele Karten muss man mindestens ziehen, um mit mindestens 90%-iger
Sicherheit mindestens einen Treffer zu landen?
(f) Wie viele Karten muss man mindestens ziehen, um mit mindestens 90%-iger
Sicherheit mindestens zwei Treffer zu landen?
(g) Eine Casino bietet das zehnmalige Kartenziehen mit Zurücklegen als Spiel an.
Der Spieler gewinnt, wenn er ein Trefferpaar (zwei Treffer hintereinander) und
sonst nur Nieten zieht. In diesem Fall erhält der Spieler den zwanzigfachen
Einsatz zurück, sonst ist der Einsatz verloren. Welche Rendite (Gewinn pro
Einsatz) wirft dieses Spiel für die Bank ab?
1
7
Lösung: Trefferwahrscheinlichkeit: p = , q = 1 − p =
8
8
3 7
−4
(a) p1 = p q = 7,67 · 10
10 3 7
(b) p2 = B(10; 18 ; 3) =
p q = 0,0920 = 9,20%
3
10 0 10
1
p q = 1 − q 10 = 0,7369 = 73,69%
(c) p3 = 1 − B(10; 8 ; 0) = 1 −
0
(d) P ( mindestens 3 Treffer“) = 1 − P ( höchstens 2 Treffer“ =⇒
”
”
p4 = B(10; 81 ; 3) + B(10; 81 ; 4) + . . . + B(10; 18 ; 10) =
= 1 − B(10; 18 ; 0) − B(10; 81 ; 1) − B(10; 18 ; 2) =
10 1 9
10 2 8
10
= 1−q −
p q −
p q = 0,1195 = 11,95%
1
2
ln 0,1
= 17,24, also mindestens 18-mal.
(e) 1 − q n ≧ 0,9 =⇒ q n ≦ 0,1 =⇒ n ≧
ln q
n 1 n−1
(f) 1 − q n −
p q
≧ 0,9 =⇒ q n + npq n−1 ≦ 0,1
|
{z
}
1
f (n)
Diese Gleichung ist für uns nur durch Probieren lösbar:
f (29) = 0,107 und f (30) = 0,0962 =⇒ mindestens 30 Karten
(g) Es gibt 9 Möglichkeiten für die Lage des Trefferpaars. Die Gewinnwahrscheinlichkeit
des Spielers ist also
pg = 9p2 q 8 = 0,04832 = 4,832%
E sei der Einsatz pro Spiel. Von N Spielen gewinnt die Bank (1 − pg )N Spiele und
nimmt somit (1 − pg )N E ein. Andererseits verliert die Bank pg N Spiele und zahlt
damit 20pg N E aus. Die Rendite der Bank ist also
(1 − pg )N E − 20pg N E
= 1 − 21pg = −1,47%
NE 4
Die Bank dürfte nur das 19-fache des Einsatzes auszahlen, dann wäre die Rendite
1 − 20pg = 3,36%
7. Ein Laplacewürfel wird n-mal geworfen.
(a) Wie groß muss n mindestens sein, damit mit mindestens 99,99%-iger Wahrscheinlichkeit mindestens ein Sechser dabei ist?
Jetzt wird der Würfel 500-mal geworfen. Wir betrachten die Ereignisse
E1 : höchstens 70 Sechser“
E3 : mindestens 78 und höchstens 93 Sechser“
”
”
E2 : mindestens 90 Sechser“ E4 : mindestens 78 und höchstens m Sechser“
”
”
(b) Die Abbildung zeigt den Grafen von b(k) = B(500, 61 , k). Veranschauliche im
Grafen die Wahrscheinlichkeiten p1 = P (E1 ) und p2 = P (E2 ) und schätze in
nachvollziehbarer Weise ihre Werte ab.
b
0,04
0,03
0,02
0,01
0,00
60
70
80
90
100
110
k
(c) Die Abbildung zeigt den Grafen von f (k) = F 1500 (k). Drücke p3 = P (E3 ) durch
6
f aus, zeichne p3 in den Grafen ein und gib den ungefähren Wert von p3 an.
Ermittle ebenfalls mit dem Grafen das kleinste m mit p4 = P (E4 ) ≧ 50%.
5
f
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,0
Lösung: (a) p =
1
6
70
=⇒
80
5
q =1−p= ,
6
n ln q ≦ −4 ln 10
(b) p1 =
70
X
k=0
p2 =
1
B 500, , k
6
500
X
k=90
1
B 500, , k
6
≈
≈
1 − q n ≧ 0,9999
=⇒
100
90
n≧
k
q n ≦ 10−4
=⇒
−4 ln 10
= 50,52
ln q
=⇒
n ≧ 51
1
· 9 · 0,0135 ≈ 6%
2
1
· 13 · 0,034 ≈ 22%
2
b
0,04
0,03
0,02
p2
0,01
p1
0,00
(c) p3 =
93
X
k=78
60
1
B 500, , k
6
70
90
80
100
110
= F 1500 (93) − F 1500 (77) = f (93) − f (77) ≈ 64%
6
6
6
k
p4 = f (m) − f (77) ≧ 0,5
=⇒
f (m) ≧ f (77) + 0,5 ≈ 0,75
=⇒
m = 89
f
0,9
0,8
0,7
0,6
p3
0,5
p4
0,5
0,4
0,3
0,2
0,1
0,0
70
80
7
90
100
k