Ziel: Berechnung krummlinig begrenzter Flächen, z

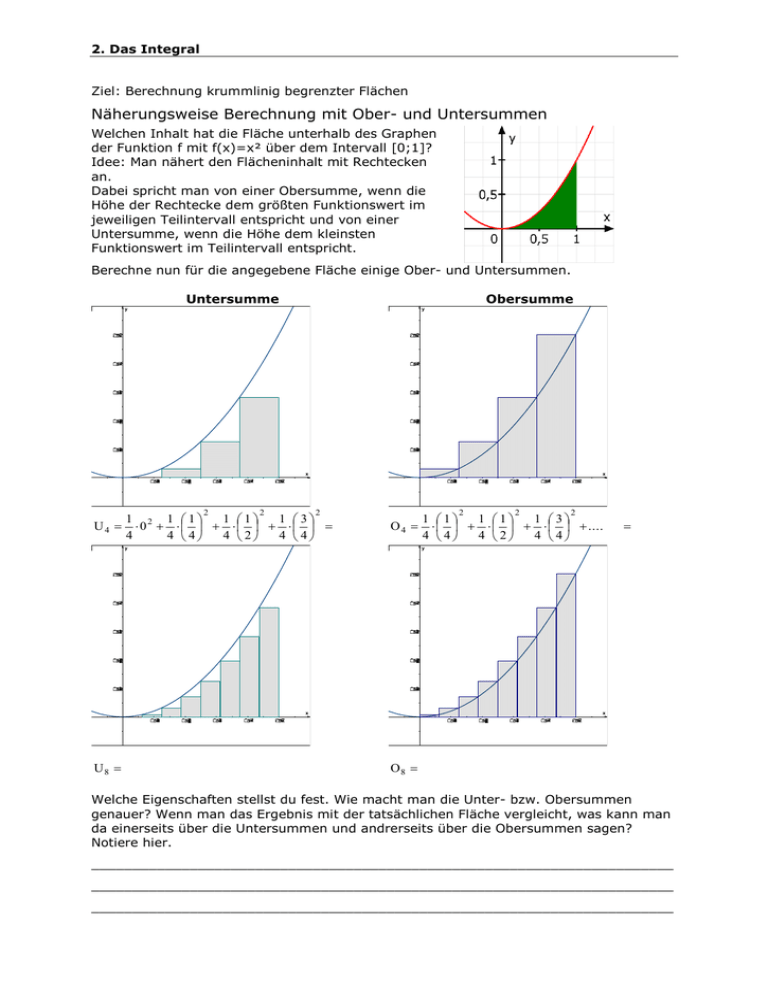
2. Das Integral
Ziel: Berechnung krummlinig begrenzter Flächen
Näherungsweise Berechnung mit Ober- und Untersummen
Welchen Inhalt hat die Fläche unterhalb des Graphen
der Funktion f mit f(x)=x² über dem Intervall [0;1]?
Idee: Man nähert den Flächeninhalt mit Rechtecken
an.
Dabei spricht man von einer Obersumme, wenn die
Höhe der Rechtecke dem größten Funktionswert im
jeweiligen Teilintervall entspricht und von einer
Untersumme, wenn die Höhe dem kleinsten
Funktionswert im Teilintervall entspricht.
Berechne nun für die angegebene Fläche einige Ober- und Untersummen.
Untersumme
Obersumme
y
y






















x








2
U4 
x





2
2
1 2 1 1
1 1
1 3
0          
4
4 4
4 2
4 4


2
O4 
y




2



2
1 1
1 1
1 3
            ....
4 4
4 2
4 4
y






















x


U8 







x














O8 
Welche Eigenschaften stellst du fest. Wie macht man die Unter- bzw. Obersummen
genauer? Wenn man das Ergebnis mit der tatsächlichen Fläche vergleicht, was kann man
da einerseits über die Untersummen und andrerseits über die Obersummen sagen?
Notiere hier.
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
2. Das Integral
Bei noch mehr Rechtecken wird es lästig das von Hand auszurechnen, also GTR:
Betrachten wir doch noch einmal U8:
2
2
2
3


1 0
1 1
1 7
1 7 2
1
U 8          ...        0 2  12  ... 7 2 
k
8 8
8 8
8 8
512 k 0
8
Mit dem GTR kann man das dann so
berechnen (die erste Eingabe mit dem seq
ist nicht notwendig, sie soll nur
verdeutlichen, was der Befehl tut, nämlich
die Folge der Quadratzahlen von 0 bis 7
auswerfen (siehe oben).
Tastenfolge für seq: 2nd stat > 5
Tastenfolge für sum: 2nd stat > > 5
In der im GTR eingegeben Formel hängen
zwei Zahlen von der 8 ab, nämlich
512=_____ und 7= ______
Wenn N=8 wäre könnte man auch
schreiben: 512=_____ und 7= ______
Oder mit GTR: siehe rechts.
Vorteil: durch Einfaches Abändern
von n kann eine neue Untersumme
berechnet werden:
2nd enter
Aufgaben
1.
Fasse alle bisherigen Ergebnisse zusammen und berechne die noch fehlenden.
n
Untersumme
4
8
16
0,273
0,303
32
Obersumme
2.
Berechne mithilfe von Unter- und Obersummen einen möglichst guten Wert für
die Fläche, welche der Graph der Funktion f mit f(x)=x³ über dem Intervall [0;1]
mit der x-Achse einschließt.
2. Das Integral
Definition des Integrals
Der gesuchte Flächeninhalt wird umso genauer berechnet, je schmäler man die
Rechtecke wählt, d. h. je größer die Anzahl der Rechtecke ist.
Dabei ist es egal, ob man Unter- oder Obersummen nimmt, man kann sogar einen ganz
beliebigen Funktionswert innerhalb des Intervalls als Höhe des Rechtecks wählen.
Deshalb definiert man:
b
lim U n  lim O n   f x dx (lies: Integral der Funktion f zwischen den Grenzen a und b)
n 
n 
a
Der Wert des Integrals entspricht also der Fläche, welche der Graph von f über dem
betrachteten Intervall mit der x-Achse einschließt. Allerdings nicht ganz: Flächen
unterhalb der x-Achse werden mit negativ bewertet. Zum Beispiel:
1
2
 x dx 
0
1
  x dx   3
1
1
3
2
0

 sinx dx  0

Der GTR kann Integrale auf zwei unterschiedliche Arten berechen: im Grafikmodus und
im Rechenfenster.
Im Grafikmodus: Aufruf des CALC-Menüs, dort Nr. 7
Im Rechenfenster: MATH-Menü, dort Nr. 9
Betrachte hierzu auch die Screenshots auf S. 92 im Buch.
Aufgaben
3.
Berechne die oben angegeben Integrale mit dem GTR auf beide möglichen Arten.
4.
Berechne auch
5.
mit den Unter- und Obersummen aus Aufgabe 1 und 2.
Aufgaben aus dem Buch: S. 93/3, 2, 4, 6, 7, 8, 9, 10, 13
1
x
1
3
dx und vergleiche dieses Ergebnis und das Ergebnis für
0
x
0
2
dx