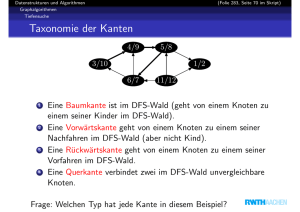
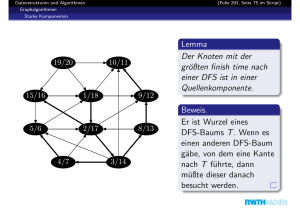
Kürzeste Wege
Werbung

Kürzeste Wege
Algorithmus von Dijkstra:
1. Es sei S die Menge der entdeckten Knoten
2. Invariante: Merke optimale Lösung für S:
Für alle v∈S sei d[v] = δ(s,v) die Länge des kürzesten
Weges von s nach v
3. Zu Beginn: S={s} und d[s]=0
4. while V≠S do
5. Wähle Knoten v∈V \ S mit mindestens einer Kante
aus S und für den d‘[v] = min d[u] + w(u,v) so klein wie
(u,v)∈E
möglich ist
6. Füge v zu S hinzu und setze d[v] ← d‘[v]
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
1
Kürzeste Wege
Wie kann man Pfade berechnen?
• Wie bei BFS/DFS über Feld π
• Wenn (u,v) die Kante ist für die das Minimum in Zeile 5
erreicht wird, dann setze π[v] ← u
• Kürzester s-u-Weg P(u) ist implizit gespeichert:
• Für u=s haben wir den leeren Weg als kürzesten Weg
von s nach s
• Für u≠s gilt:
P(u) besteht aus Weg P(π(u)) gefolgt von Kante (π[u],u)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
2
Kürzeste Wege
Satz 14.14 (Korrektheit):
(Invariante) Für jedes u∈S ist zu jedem Zeitpunkt der
Ausführung des Algorithmus der Weg P(u) ein kürzester
s-u-Weg.
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
3
Kürzeste Wege
Wie kann man Dijkstras Algorithmus effizient
implementieren?
• Naiver Ansatz: Überprüfe für jeden Knoten aus V-S alle
Kanten (Laufzeit O(|V|⋅|E|) in jedem Durchlauf)
Besser:
• Halte d‘[v] Werte für alle v∈V-S aufrecht
• Speichere alle Knoten aus V-S in Prioritätenschlange ab
mit Schlüssel d‘[v]
• Problem: Was ist, wenn sich Schlüssel verändern
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
4
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
5
Decrease-Key(A,i,newkey)
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
SS 2008
9
11
12
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
15
5
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
5
Decrease-Key(A,i,newkey)
9
11
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
15
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
6
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
5
Decrease-Key(A,i,newkey)
9
11
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
3 i
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
7
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
5
Decrease-Key(A,i,newkey)
9
11
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
3 i
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
8
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
5
Decrease-Key(A,i,newkey)
9
3
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
11 i
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
9
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
5
Decrease-Key(A,i,newkey)
9
3 i
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
11
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
10
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
5
Decrease-Key(A,i,newkey)
9
3 i
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
11
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
11
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
3
Decrease-Key(A,i,newkey)
9
5 i
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
11
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
12
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
3
i
Decrease-Key(A,i,newkey)
9
5
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
11
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
13
Kürzeste Wege
Heaps mit Decrease-Key:
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
3
i
Decrease-Key(A,i,newkey)
9
5
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
11
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
14
Kürzeste Wege
Heaps mit Decrease-Key:
Laufzeit: O(log n)
• Datenstruktur Min-Heap A
• Neue Funktion DecreaseKey(A, i, newkey):
Wir bekommen Index i des Elements des Heaps, dessen
Wert (Schlüssel) auf den Wert newkey
• newkey ist kleiner als der alte Schlüssel
3
i
Decrease-Key(A,i,newkey)
9
5
1. A[i] ← newkey
2. while i>1 and A[parent[i]]>A[i] do
11
12
3. A[parent[i]] ↔ A[i]
4. i ← parent[i]
DecreaseKey(A,5,3)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
15
Kürzeste Wege
Wie kann man Dijkstras Algorithmus effizient
implementieren?
• Halte d‘[v] Werte für alle v∈V-S aufrecht
• Speichere alle Knoten aus V-S in Prioritätenschlange ab
mit Schlüssel d‘[v]
• Für jeden Knoten v speichere Zeiger auf sein
Vorkommen im Heap
• d‘[v] Werte vergrößern sich nie
• Benutze Decrease-Key, wenn sich Wert d‘[v] verringert
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
16
Kürzeste Wege
Dijkstra(G,w,s)
1. for each vertex v∈V do d[v]←∞; d‘[v]←∞; π[v]←nil
2. d‘[s]←0; S←∅; Q←V
3. while Q≠∅ do
4. u←Extract-Min(Q)
5. d[u]←d‘[u]; S←S∪{u}
6. for each vertex v∈Adj[u] do
7.
if d‘[v]>d[u]+w(u,v) then d‘[v]←d[u]+w(u,v); π[v]←u
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
17
Kürzeste Wege
Dijkstra(G,w,s)
1. for each vertex v∈V do d[v]←∞; π[v]←nil
2. d[s]←0; S←∅; Q←V
Beobachtung:
3. while Q≠∅ do
Wir können Felder d und d‘ durch
4. u←Extract-Min(Q)
ein Feld d ersetzen, weil d nur für
Knoten aus S benutzt wird und d‘ nur
5. S←S∪{u}
für Knoten aus V-S.
6. for each vertex v∈Adj[u] do
7.
if d[v]>d[u]+w(u,v) then d[v]←d[u]+w(u,v); π[v]←u
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
18
Kürzeste Wege
Dijkstra(G,w,s)
1. for each vertex v∈V do d[v]←∞; π[v]←nil
2. d[s]←0; S←∅; Q←V
Hier muß zusätzlich noch eine
3. while Q≠∅ do
Decrease-Key Operation
4. u←Extract-Min(Q)
durchgeführt werden, da Q ein
Min-Heap mit den d-Werten der
5. S←S∪{u}
Knoten als Schlüssel ist.
6. for each vertex v∈Adj[u] do
7.
if d[v]>d[u]+w(u,v) then d[v]←d[u]+w(u,v); π[v]←u
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
19
Kürzeste Wege
2
a
2 4
s
7
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
c
2
1
b
6 8
d
5
20
Kürzeste Wege
2
a
2 4
s
∞
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
∞
7
c
∞
2
1
5
∞
b
6 8
d
∞
21
Kürzeste Wege
2
s
s
Q:
a
c
SS 2008
b
a
∞
2 4
0
7
c
∞
2
1
5
∞
b
6 8
d
∞
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
22
Kürzeste Wege
2
s
s
Q:
a
c
SS 2008
b
a
∞
2 4
0
7
c
∞
2
1
5
∞
b
6 8
d
∞
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
23
Kürzeste Wege
2
s
d
Q:
a
b
a
∞
2 4
0
7
c
∞
2
1
5
∞
b
6 8
d
∞
c
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
24
Kürzeste Wege
2
s
d
Q:
a
b
a
∞
2 4
0
7
c
∞
2
1
5
∞
b
6 8
d
∞
c
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
25
Kürzeste Wege
2
s
d
Q:
a
b
a
∞
2 4
0
7
c
∞
2
1
5
∞
b
6 8
d
∞
c
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
26
Kürzeste Wege
2
s
a
Q:
d
b
a
2
2 4
0
7
c
∞
2
1
5
∞
b
6 8
d
∞
c
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
27
Kürzeste Wege
2
s
a
Q:
d
b
a
2
2 4
0
7
c
∞
2
1
5
∞
b
6 8
d
∞
c
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
28
Kürzeste Wege
2
s
a
Q:
c
b
a
2
2 4
0
7
c
7
2
1
5
∞
b
6 8
d
∞
d
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
29
Kürzeste Wege
2
s
a
Q:
c
b
a
2
2 4
0
7
c
7
2
1
5
∞
b
6 8
d
∞
d
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
30
Kürzeste Wege
2
s
c
Q:
d
SS 2008
b
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
7
2
1
5
∞
b
6 8
d
∞
31
Kürzeste Wege
2
s
c
Q:
d
SS 2008
b
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
7
2
1
5
∞
b
6 8
d
∞
32
Kürzeste Wege
2
s
b
Q:
d
SS 2008
c
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
7
2
1
5
4
b
6 8
d
∞
33
Kürzeste Wege
2
s
b
Q:
d
SS 2008
c
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
7
2
1
5
4
b
6 8
d
∞
34
Kürzeste Wege
2
s
b
Q:
d
SS 2008
c
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
35
Kürzeste Wege
2
s
b
Q:
d
SS 2008
c
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
36
Kürzeste Wege
2
s
c
Q:
d
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
37
Kürzeste Wege
2
s
c
Q:
d
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
38
Kürzeste Wege
2
s
c
Q:
d
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
39
Kürzeste Wege
2
s
c
Q:
d
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
40
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
41
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
42
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
43
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
44
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
45
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
46
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
d
∞
47
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
9
48
d
Kürzeste Wege
2
s
Q:
SS 2008
d
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
9
49
d
Kürzeste Wege
2
s
Q:
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
9
50
d
Kürzeste Wege
2
s
Q:
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
9
51
d
Kürzeste Wege
2
s
Q:
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
9
52
d
Kürzeste Wege
2
s
Q:
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
a
2
2 4
0
7
c
4
2
1
5
4
b
6 8
9
53
d
Kürzeste Wege
Dijkstra(G,w,s)
1. for each vertex v∈V do d[v]←∞; π[v]←nil
4
2
2
2. d[s]←0; S←∅; Q←V
a
b
2
3. while Q≠∅ do
1
2
4
s
6 8
4. u←Extract-Min(Q)
0
7
5. S←S∪{u}
d
c
5
9
4
6. for each vertex v∈Adj[u] do
7.
if d[v]>d[u]+w(u,v) then d[v]←d[u]+w(u,v); π[v]←u
Laufzeit: O((|V| + |E|) log |V|)
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
54
Kürzeste Wege
Dijkstras Algorithmus
• Kürzeste Wege von einem Knoten und mit positiven
Kantengewichten
• Laufzeit O((|V|+|E|) log |V|)
• Bessere Laufzeit von O(|V| log |V| + |E|) möglich mit
besseren Prioritätenschlangen
Fragen:
• Was passiert bei negativen Kantengewichten?
• Wie kann man das kürzeste Wege Problem für alle
Paare von Knoten effizient lösen?
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
55
Kürzeste Wege
Das transitive Hülle Problem:
• Gegeben sei ein gerichteter, ungewichteter Graph G=(V,E)
• Gesucht: Die transitive Hülle G*=(V,E*) von G, wobei
E*={(u,v): es gibt Weg von u nach v in G}
G
SS 2008
G*
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
56
Kürzeste Wege
Transitive Hülle:
• In O(|V|²+|V| |E|) Zeit mit Breiten- oder Tiefensuche von
jedem Knoten
• Geht das auch schneller?
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
57
Kürzeste Wege
Graphen und Matrixmultiplikation:
• Sei A die n×n-Adjazenzmatrix von Graph G mit
Knotenmenge {1,…,n}
• Was ist A⋅A?
Behauptung 14.15:
Sei Z= A⋅A. Dann gilt zij >0, g.d.w. es in G einen Pfad der
Länge 2 von Knoten i zu Knoten j gibt.
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
58
Kürzeste Wege
Behauptung 14.16:
Sei Z‘= A⋅A + A. Dann gilt, dass z‘ij >0, g.d.w. es einen Weg
der Länge 1 oder 2 von Knoten i zu Knoten j gibt.
Konstruiere Matrix B mit:
• bij =1 ⇔ z‘ij >0
Behauptung 14.17:
Matrix B hat einen Weg von Knoten i nach j, g.d.w. Matrix A
einen solchen Weg hat.
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
59
Kürzeste Wege
Behauptung 14.18:
Sei P ein Weg der Länge k>1 in G. Dann hat P maximal
Länge 2/3 k in dem von Matrix B beschriebenen Graph G‘.
Konsquenz aus Beh. 14.17 und 14.18:
• Wenn wir die Berechnung von B log 3/2 n mal iterieren,
haben wir die transitive Hülle berechnet
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
60
Kürzeste Wege
TransitiveHülle(A)
1. for i←1 to log3/2n do
2. Z‘ ← A A+A
3. for i←1 to n do
4.
for j←1 to n do
5.
if z‘ij >0 then bij ←1 else bij ←0
6. A←B
7. return A
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
61
Kürzeste Wege
Satz 14.19:
Der Algorithmus TransitiveHülle berechnet die transitive
Hülle eines Graphen G in
O(M(n) log n) Zeit, wobei M(n) die Laufzeit zur
Matrixmultiplikation bezeichnet.
SS 2008
Datenstrukturen und Algorithmen
14. Elementare Graphalgorithmen
62