LB 2 - meinelt

LB 2: Gebrochen rationale Funktionen - Lösungen
1
1+ x
a) Definitionsbereich: D f = R \ {−1}
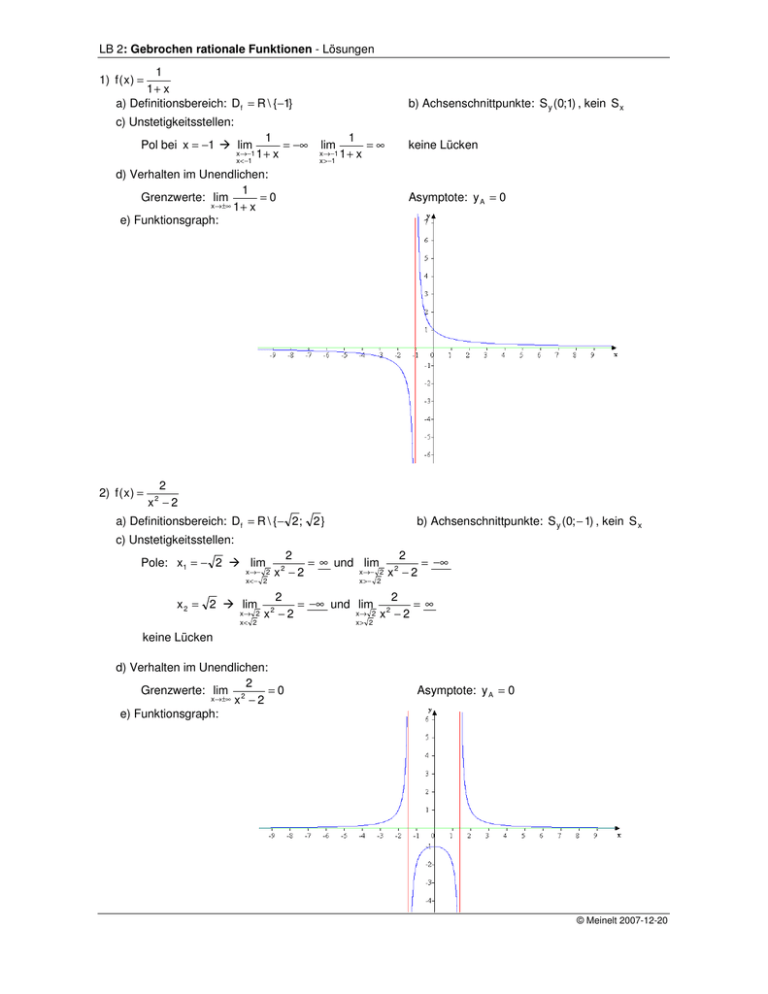
1) f ( x ) =
b) Achsenschnittpunkte: S y (0;1) , kein S x
c) Unstetigkeitsstellen:
Pol bei x = −1 lim
x → −1
x < −1
1
= −∞
1+ x
lim
x → −1
x > −1
1
=∞
1+ x
d) Verhalten im Unendlichen:
1
Grenzwerte: lim
=0
x → ±∞ 1 + x
e) Funktionsgraph:
2) f ( x ) =
keine Lücken
Asymptote: y A = 0
2
x2 − 2
b) Achsenschnittpunkte: S y (0; − 1) , kein S x
a) Definitionsbereich: D f = R \ {− 2 ; 2 }
c) Unstetigkeitsstellen:
Pole: x1 = − 2 lim
x →− 2
x< − 2
2
2
= ∞ und lim 2
= −∞
x →− 2 x − 2
x2 − 2
x >− 2
2
2
= −∞ und lim 2
= ∞
x 2 = 2 lim 2
x→ 2 x − 2
x→ 2 x − 2
x< 2
x> 2
keine Lücken
d) Verhalten im Unendlichen:
2
Grenzwerte: lim 2
=0
x →±∞ x − 2
e) Funktionsgraph:
Asymptote: y A = 0
© Meinelt 2007-12-20
LB 2: Gebrochen rationale Funktionen - Lösungen
x+3
x−3
a) Definitionsbereich: Df = R \ {3}
3) f ( x ) =
b) Achsenschnittpunkte: S y (0; − 1) , S x ( −3; 0)
c) Unstetigkeitsstellen:
Pol bei x = 3 lim
x →3
x <3
x+3
x+3
= −∞ lim
=∞
x →3 x − 3
x−3
x >3
d) Verhalten im Unendlichen:
x+3
Grenzwerte: lim
=1
x → ±∞ x − 3
e) Funktionsgraph:
keine Lücken
Asymptote: y A = 1
x−4
x−4
=
x 2 − 3 x − 4 (x − 4) ⋅ (x + 1)
a) Definitionsbereich: Df = R \ {−1; 4}
4) f ( x ) =
b) Achsenschnittpunkte: S y (0;1) , kein S x
c) Unstetigkeitsstellen:
Pol: x = −1 lim
x → −1
x < −1
1
= −∞
x +1
d) Verhalten im Unendlichen:
1
Grenzwerte: lim
=0
x → ±∞ x + 1
e) Funktionsgraph:
lim
x → −1
x > −1
1
=∞
x +1
Lücke: x = 4 lim
x→4
1
= 0,2
x +1
Asymptote: y A = 0
© Meinelt 2007-12-20
LB 2: Gebrochen rationale Funktionen - Lösungen
5) f ( x ) =
2x 2 − 1
x2 − 2
a) Definitionsbereich: D f = R \ { − 2 ; 2 }
b) Achsenschnittpunkte: S y (0; 21 ) , S x1( −
1 ; 0) ,
2
S x1(
1
; 0)
2
c) Unstetigkeitsstellen:
- Pole: x1 = − 2 x 2 = 2
lim
3 x 2 − 12
3 x 2 − 12
3 x 2 − 12
3 x 2 − 12
= ∞ und lim
= −∞ bzw. lim
= −∞ und lim
=∞
2
2
2
2
2 2x − 4
x →− 2 2 x − 4
x→ 2 2x − 4
x→ 2 2x − 4
x →−
x< − 2
x>− 2
x< 2
x> 2
- keine Lücken
d) Verhalten im Unendlichen:
2x 2 − 1
Grenzwerte: lim 2
=2
x → ±∞ x − 2
e) Funktionsgraph:
Asymptote: y A = 2
2
x 2 − 2 x + 1 (x − 1)
= 2
x2 + 1
x +1
a) Definitionsbereich: D f = R
6) f ( x ) =
c) Unstetigkeitsstellen: keine
d) Verhalten im Unendlichen:
x 2 − 2x + 1
Grenzwerte: lim
=1
x→ ±∞
x2 + 1
e) Funktionsgraph:
b) Achsenschnittpunkte: S y (0;1) , S x (1; 0 )
Asymptote: y A = 1
© Meinelt 2007-12-20
LB 2: Gebrochen rationale Funktionen - Lösungen
(x + 2) ⋅ (x − 2)
x2 − 4
=
x + x − 2 (x + 2) ⋅ (x − 1)
a) Definitionsbereich: D f = R \ { −2; 1}
7) f ( x ) =
2
b) Achsenschnittpunkte: S y (0; 2) , S x (2; 0)
c) Unstetigkeitsstellen:
x−2
x−2
Pol: x = 1 lim
= ∞ lim
= −∞
x→1 x − 1
x →1 x − 1
x<1
x >1
Lücke: x = −2 lim
d) Verhalten im Unendlichen:
x−2
Grenzwerte: lim
=1
x → ±∞ x − 1
e) Funktionsgraph:
Asymptote: y A = 1
x → −2
x−2 4
=
x −1 3
2
8) f ( x ) =
(x − 2) ⋅ (x + 1)
x 3 − 3x 2 + 4
=
(x − 2) ⋅ (2x − 1) ⋅ x 2 + 1 (x − 2) ⋅ (2x − 1) ⋅ x 2 + 1
(
)
(
1
2
a) Definitionsbereich: D f = R \ { ; 2}
)
b) Achsenschnittpunkte: S y (0; 2) , S x ( −1; 0)
c) Unstetigkeitsstellen:
Pol: x =
1
2
(x − 2) ⋅ (x + 1) = ∞ lim (x − 2) ⋅ (x + 1) = −∞
x→0,5 (2 x − 1) ⋅ (x 2 + 1)
(2x − 1) ⋅ (x 2 + 1)
x >0,5
(
x − 2) ⋅ (x + 1)
lim
=0
x→−2 (2 x − 1) ⋅ (x 2 + 1)
lim
x→0,5
x<0,5
Lücke: x = 2 d) Verhalten im Unendlichen:
x 3 − 3x 2 + 4
Grenzwerte: lim
=0
x →±∞ 2 x 4 − 5 x 3 + 4 x 2 − 5 x + 2
e) Funktionsgraph:
Asymptote: y A = 0
© Meinelt 2007-12-20
LB 2: Gebrochen rationale Funktionen - Lösungen
9) f ( x ) =
(x
2
)(
) (
(
)(
)
− 1 ⋅ x2 − 3
x2 − 1 ⋅ x2 − 3
=
2
x − x − x +1
x 2 − 1 ⋅ (x − 1)
3
a) Definitionsbereich: D f = R \ {−1; 1}
c) Unstetigkeitsstellen:
x2 − 3
=∞
Pol: x = 1 lim
x →1 x − 1
x <1
)
b) Achsenschnittpunkte: S y (0; 3) , S x1( − 3 ; 0 ) , S x 2 ( 3 ; 0)
x2 − 3
= −∞
x →1 x − 1
x >1
lim
x2 − 3
=1
x −1
d) Verhalten im Unendlichen:
x2 − 3
Grenzwerte: lim
= ±∞
x → ±∞ x − 1
e) Funktionsgraph:
Lücke: x = −1 lim
x → −1
Asymptote: ( x 2 − 3) : ( x − 1) = x + 1 −
2
yA = x + 1
x −1
© Meinelt 2007-12-20
LB 2: Gebrochen rationale Funktionen - Lösungen
(
)
x 4 − 5 x 3 + 2x 2 − 10 x x ⋅ (x − 5 ) ⋅ x 2 − 4
=
x 4 − 5x 2 + 4
x2 − 1 ⋅ x2 − 4
a) DB: D f = R \ { −2; − 1; 1; 2}
b) Achsenschnittpunkte: S y (0; 0) , S x1(0; 0 ) , S x 2 (5; 0)
10) f ( x ) =
(
)(
)
c) Unstetigkeitsstellen:
x ⋅ (x − 5 )
x ⋅ (x − 5 )
= ∞ lim
= −∞
x→−1 (x − 1) ⋅ (x + 1)
(x − 1) ⋅ (x + 1)
x > −1
x ⋅ (x − 5 )
x ⋅ (x − 5 )
= ∞ lim
= −∞
x 2 = 1 lim
x →1 (x − 1) ⋅ (x + 1)
x →1 (x − 1) ⋅ (x + 1)
x <1
x >1
x ⋅ (x − 5 ) 14
=
≈ 4,67
Lücken: x = −2 lim
Pole:
x1 = −1 lim
x→ −1
x< −1
1
x → −2
(x
2
)
−1
3
x ⋅ (x − 5 )
= −2
x1 = 2 lim
x →2
x2 − 1
d) Verhalten im Unendlichen:
x 4 − 5 x 3 + 2x 2 − 10 x
Grenzwerte: lim
=1
x→ ±∞
x 4 + 2x 2 − 3
e) Funktionsgraph:
(
)
Asymptote: y A = 1
© Meinelt 2007-12-20