LU 6 Theorie Koordinaten, Kongruenzabbildungen

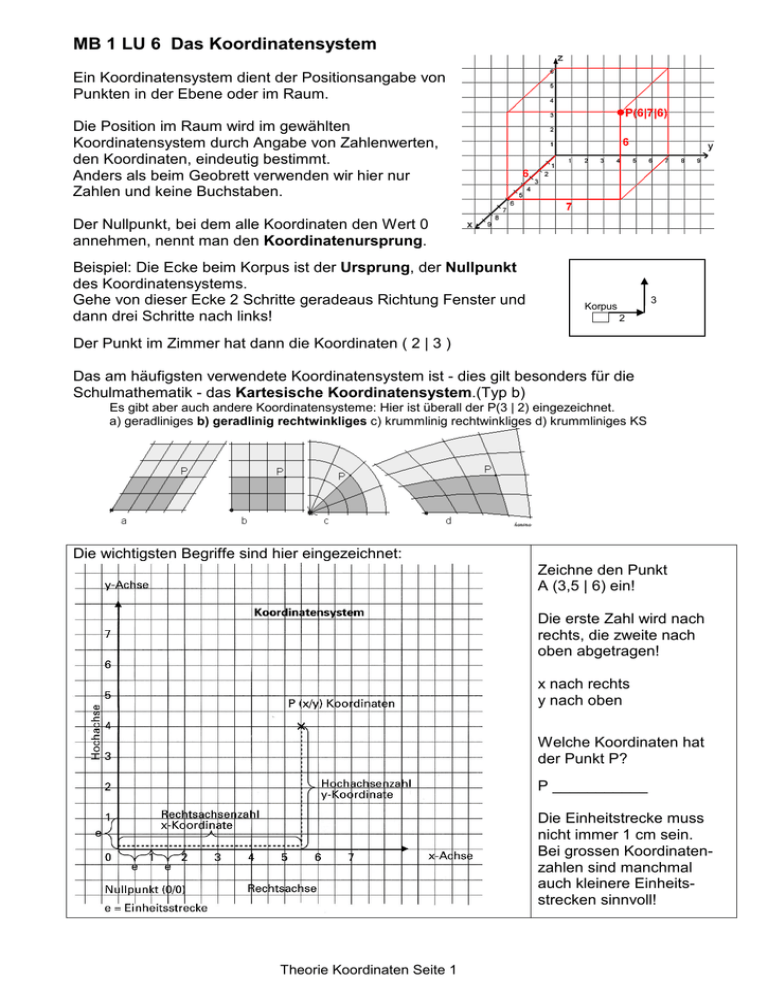
MB 1 LU 6 Das Koordinatensystem
Ein Koordinatensystem dient der Positionsangabe von
Punkten in der Ebene oder im Raum.
Die Position im Raum wird im gewählten
Koordinatensystem durch Angabe von Zahlenwerten,
den Koordinaten, eindeutig bestimmt.
Anders als beim Geobrett verwenden wir hier nur
Zahlen und keine Buchstaben.
Der Nullpunkt, bei dem alle Koordinaten den Wert 0
annehmen, nennt man den Koordinatenursprung.
Beispiel: Die Ecke beim Korpus ist der Ursprung, der Nullpunkt
des Koordinatensystems.
Gehe von dieser Ecke 2 Schritte geradeaus Richtung Fenster und
dann drei Schritte nach links!
3
Korpus
2
Der Punkt im Zimmer hat dann die Koordinaten ( 2 | 3 )
Das am häufigsten verwendete Koordinatensystem ist - dies gilt besonders für die
Schulmathematik - das Kartesische Koordinatensystem.(Typ b)
Es gibt aber auch andere Koordinatensysteme: Hier ist überall der P(3 | 2) eingezeichnet.
a) geradliniges b) geradlinig rechtwinkliges c) krummlinig rechtwinkliges d) krummliniges KS
Die wichtigsten Begriffe sind hier eingezeichnet:
Zeichne den Punkt
A (3,5 | 6) ein!
Die erste Zahl wird nach
rechts, die zweite nach
oben abgetragen!
x nach rechts
y nach oben
Welche Koordinaten hat
der Punkt P?
P ___________
Die Einheitstrecke muss
nicht immer 1 cm sein.
Bei grossen Koordinatenzahlen sind manchmal
auch kleinere Einheitsstrecken sinnvoll!
Theorie Koordinaten Seite 1
Trage die Punkte richtig ein!
A (4 | 3), B (2,5 | 5), C (5 | 5), D (5,5 | 4,5) E (6,5 | 4,5), F (6,5 | 6), G (7,5 | 6), H (8 | 7),
I (8,5 | 7), K (8 | 6), L (9 | 6), M (9 | 4,5), N (11,5 | (4,5), O (10,5 | 3)
Das Koordinatensystem funktioniert natürlich auch mit negativen Zahlen:
1. Kongruenzabbildungen
(Kongruent heisst Deckungsgleich, Form und Grösse der Figur bleibt gleich)
a) Verschiebung
Trage die folgenden Punkte ein und verbinde sie: A (-5 | -3), B (-2 | -1), C (-4 | -1), D (-5 | 1)
Abbildungsvorschrift: Addiere zu den x-Koordinaten 6 und zu den y-Koordinaten 2 !
Theorie Koordinaten Seite 2
b) Achsenspiegelung
Trage die Punkte ein und verbinde sie: A (-4 | -1), B (-2 | 0), C (-1 | 2), D (-4 | 3)
Abbildungsvorschrift: Spiegle die Figur an der Spiegelachse!
Spiegelachse
Was passiert mit den Koordinaten? _________________________________________
c) Punktspiegelung
Trage die Punkte ein und verbinde sie: A (-5 | 2), B (-2 | 1), C (-1 | 3), D (-3 | 3) , E (-3 | 2)
Abbildungsvorschrift: Spiegle die Punkte am Ursprung!
Was passiert mit den Koordinaten? _________________________________________
Theorie Koordinaten Seite 3
d) Drehung
Trage die Punkte ein und verbinde sie: A (-5 | 1), B (-3 | 1), C (-3 | 2), D (-2 | 2) , E (-4 | 4)
Abbildungsvorschrift: Drehe die Figur um 90° gegen den Uhrzeiger!
Was passiert mit den Koordinaten? _________________________________________
2. Ähnlichkeitsabbildung (Form bleibt gleich, Grösse ändert sich)
Streckung
Trage die Punkte ein und verbinde sie: A (-2 | -1), B (1 | 0), C (2 | -2), D (2 | 1) , E (-1 | 1)
Abbildungsvorschrift: Verdreifache alle Koordinaten!
Theorie Koordinaten Seite 4
Entwürfe
Theorie Koordinaten Seite 5
Theorie Koordinaten Seite 6