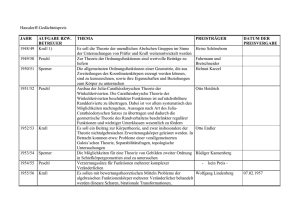
Eine objektorientierte Programmierumgebung für

1
Eine objektorientierte Programmierumgebung
für differentialgeometrische Berechnungen in
MuPAD
Studienarbeit von
WOLFGANG G LOBKE
Betreuer:
Dipl. Inf. Marcus Hausdorf
Dr. Werner Seiler
Institut für Algorithmen und kognitive Systeme
Lehrstuhl Prof. Dr. Jacques Calmet
Universität Karlsruhe
2
Ziele der Arbeit
Entwicklung von Datenstrukturen für
differentialgeometrische Berechnungen in MuPAD.
Anpassen dieser Datenstrukturen an die
detools-Bibliothek.
Datenstrukturen für Jetbündel.
3
Übersicht
1
Objektorientierung in MuPAD
2
Mannigfaltigkeiten
3
Vektorfelder und Differentialformen
4
Differentialgleichungen
5
Beispiel: Die Monge-Ampère-Gleichung
4
Gliederung
1
Objektorientierung in MuPAD
2
Mannigfaltigkeiten
3
Vektorfelder und Differentialformen
4
Differentialgleichungen
5
Beispiel: Die Monge-Ampère-Gleichung
5
Kategorien und Domänen in MuPAD
Zwei wesentliche Konzepte zur OO-Programmierung in
MuPAD:
Kategorien
Grobe Entsprechung der mathematischen Kategorien.
Abstrakte Schnittstellen (≈ Interface in Java).
Ein Objekt kann zu mehreren Kategorien gehören.
Domänen
Stellen konkrete Datentypen bzw. mathematische
Strukturen dar.
Instanzen können erzeugt werden (≈ Class in Java).
Ein Objekt gehört zu höchstens einer Domäne, aber
einfache Vererbung möglich.
6
Kategorien und Domänen in MuPAD
Zwei wesentliche Konzepte zur OO-Programmierung in
MuPAD:
Kategorien
Grobe Entsprechung der mathematischen Kategorien.
Abstrakte Schnittstellen (≈ Interface in Java).
Ein Objekt kann zu mehreren Kategorien gehören.
Domänen
Stellen konkrete Datentypen bzw. mathematische
Strukturen dar.
Instanzen können erzeugt werden (≈ Class in Java).
Ein Objekt gehört zu höchstens einer Domäne, aber
einfache Vererbung möglich.
7
Kategorien und Domänen in MuPAD
Zwei wesentliche Konzepte zur OO-Programmierung in
MuPAD:
Kategorien
Grobe Entsprechung der mathematischen Kategorien.
Abstrakte Schnittstellen (≈ Interface in Java).
Ein Objekt kann zu mehreren Kategorien gehören.
Domänen
Stellen konkrete Datentypen bzw. mathematische
Strukturen dar.
Instanzen können erzeugt werden (≈ Class in Java).
Ein Objekt gehört zu höchstens einer Domäne, aber
einfache Vererbung möglich.
8
Gliederung
1
Objektorientierung in MuPAD
2
Mannigfaltigkeiten
3
Vektorfelder und Differentialformen
4
Differentialgleichungen
5
Beispiel: Die Monge-Ampère-Gleichung
9
Mannigfaltigkeiten: Rechnen in Koordinaten
M
p
ξ
x = ξ(p)
n
Rechnen auf Mannigfaltigkeiten: Lokal über Karten in
offenen Teilmenge des n abbilden und dort rechnen.
R
Identifiziere p ∈ M mit seinen Koordinaten x ∈
werden nur noch Koordinaten angegeben.
Rn ; es
10
Mannigfaltigkeiten in MuPAD
C
D
o
m
:
:
M
a
n
i
f
o
l
d
a
t
:
:
M
a
n
i
f
o
l
d
D
o
m
:
:
S
u
b
M
a
n
i
f
o
l
d
Cat::Manifold: Nur Schnittstelle, keine
Implementierung.
Dom::Manifold: Liste von Koordinaten; Methoden für
Jetbündel.
Dom::SubManifold: Implizite Untermannigfaltigkeiten;
Methoden für Tangentialräume.
11
Abbildungen zwischen Mannigfaltigkeiten
C
D
a
o
t
m
:
:
:
M
:
a
M
n
a
i
n
f
o
i
f
l
o
d
M
l
d
a
M
p
a
p
Cat::ManifoldMap(M1,M2,R): Abbildungen zwischen
Mannigfaltigkeiten F : M1 → M2 mit Koeffizienten aus R.
Implementiert bereits die meisten mathematischen
Methoden.
Dom::ManifoldMap(M1,M2,R): Stellt einige
administrative Methoden bereit.
12
Abbildungen zwischen Mannigfaltigkeiten
Eigenschaften von Cat::ManifoldMap(M1,M2,R):
R gehört zur Kategorie Cat::DifferentialRing.
Wahl von R ermöglicht Ausnutzen von spezieller Arithmetik.
Differentiale dF berechnen.
Pullbacks F ∗ von Abbildungen, Vektorfeldern und
Differentialformen berechnen.
Immersierte und eingebettete Untermannigfaltigkeiten
durch Abbildungen darstellen.
13
Abbildungen zwischen Mannigfaltigkeiten
Eigenschaften von Cat::ManifoldMap(M1,M2,R):
R gehört zur Kategorie Cat::DifferentialRing.
Wahl von R ermöglicht Ausnutzen von spezieller Arithmetik.
Differentiale dF berechnen.
Pullbacks F ∗ von Abbildungen, Vektorfeldern und
Differentialformen berechnen.
Immersierte und eingebettete Untermannigfaltigkeiten
durch Abbildungen darstellen.
14
Abbildungen zwischen Mannigfaltigkeiten
Eigenschaften von Cat::ManifoldMap(M1,M2,R):
R gehört zur Kategorie Cat::DifferentialRing.
Wahl von R ermöglicht Ausnutzen von spezieller Arithmetik.
Differentiale dF berechnen.
Pullbacks F ∗ von Abbildungen, Vektorfeldern und
Differentialformen berechnen.
Immersierte und eingebettete Untermannigfaltigkeiten
durch Abbildungen darstellen.
15
Abbildungen zwischen Mannigfaltigkeiten
Eigenschaften von Cat::ManifoldMap(M1,M2,R):
R gehört zur Kategorie Cat::DifferentialRing.
Wahl von R ermöglicht Ausnutzen von spezieller Arithmetik.
Differentiale dF berechnen.
Pullbacks F ∗ von Abbildungen, Vektorfeldern und
Differentialformen berechnen.
Immersierte und eingebettete Untermannigfaltigkeiten
durch Abbildungen darstellen.
16
Abbildungen zwischen Mannigfaltigkeiten
Eigenschaften von Cat::ManifoldMap(M1,M2,R):
R gehört zur Kategorie Cat::DifferentialRing.
Wahl von R ermöglicht Ausnutzen von spezieller Arithmetik.
Differentiale dF berechnen.
Pullbacks F ∗ von Abbildungen, Vektorfeldern und
Differentialformen berechnen.
Immersierte und eingebettete Untermannigfaltigkeiten
durch Abbildungen darstellen.
17
Abbildungen zwischen Mannigfaltigkeiten
Eigenschaften von Cat::ManifoldMap(M1,M2,R):
R gehört zur Kategorie Cat::DifferentialRing.
Wahl von R ermöglicht Ausnutzen von spezieller Arithmetik.
Differentiale dF berechnen.
Pullbacks F ∗ von Abbildungen, Vektorfeldern und
Differentialformen berechnen.
Immersierte und eingebettete Untermannigfaltigkeiten
durch Abbildungen darstellen.
18
Gliederung
1
Objektorientierung in MuPAD
2
Mannigfaltigkeiten
3
Vektorfelder und Differentialformen
4
Differentialgleichungen
5
Beispiel: Die Monge-Ampère-Gleichung
19
Vektorfelder und Differentialformen
Bereits im detools-Paket vorhanden:
D
D
D
o
o
m
m
:
:
:
J
:
V
e
e
t
c
V
t
e
o
c
r
t
F
o
i
r
e
F
l
i
o
m
:
:
F
r
e
e
M
o
d
u
l
e
O
l
d
d
e
D
l
d
D
o
o
m
m
:
:
:
:
E
D
x
i
f
t
e
r
f
e
r
i
e
o
r
n
A
t
l
i
a
g
e
l
F
b
o
r
r
a
m
Dom::VectorField: Vektorfelder auf Mannigfaltigkeiten.
Dom::JetVectorField: Vektorfelder auf Jetbündel;
stellt Methoden zur Symmetrieanalyse bereit.
Dom::DifferentialForm: Differentialformen auf
Mannigfaltigkeiten.
20
Vektorfelder und Differentialformen
Details zu Vektorfeldern und Differentialformen:
Wahl des Koeffizientenrings erlaubt spezielle Arithmetik.
Datenstrukturen angepasst an Dom::Manifold.
Geometrische Operationen:
Innere Ableitung X yω.
Äußeres Differential dω.
Kommutator [X , Y ] und Lie-Ableitung LX (ω), LX (Y ).
21
Vektorfelder und Differentialformen
Details zu Vektorfeldern und Differentialformen:
Wahl des Koeffizientenrings erlaubt spezielle Arithmetik.
Datenstrukturen angepasst an Dom::Manifold.
Geometrische Operationen:
Innere Ableitung X yω.
Äußeres Differential dω.
Kommutator [X , Y ] und Lie-Ableitung LX (ω), LX (Y ).
22
Vektorfelder und Differentialformen
Details zu Vektorfeldern und Differentialformen:
Wahl des Koeffizientenrings erlaubt spezielle Arithmetik.
Datenstrukturen angepasst an Dom::Manifold.
Geometrische Operationen:
Innere Ableitung X yω.
Äußeres Differential dω.
Kommutator [X , Y ] und Lie-Ableitung LX (ω), LX (Y ).
23
Vektorfelder und Differentialformen
Details zu Vektorfeldern und Differentialformen:
Wahl des Koeffizientenrings erlaubt spezielle Arithmetik.
Datenstrukturen angepasst an Dom::Manifold.
Geometrische Operationen:
Innere Ableitung X yω.
Äußeres Differential dω.
Kommutator [X , Y ] und Lie-Ableitung LX (ω), LX (Y ).
24
Gliederung
1
Objektorientierung in MuPAD
2
Mannigfaltigkeiten
3
Vektorfelder und Differentialformen
4
Differentialgleichungen
5
Beispiel: Die Monge-Ampère-Gleichung
25
Differentialgleichungen
System S von Differentialgleichungen:
Fk (x, u (q) ) = 0,
k = 1, . . . , s.
Unabhängige Variablen x ∈ X .
Abhängige Variablen u (q) ∈ U (q) mit partiellen Ableitungen
bis zur Ordnung q.
Lösung hat die Form u = f (x).
26
Jetbündel
Fasse abhängige Variablen als freie Parameter auf:
Das Jetbündel der Ordnung q über X und U ist
Jq (X , U) = X × U (q) .
Für f : X → U ist die q-te Prolongation
jq f : X → Jq (X , U),
x 7→ (x, f (x ), . . . ∂µf (x) . . .).
Fasse S als implizite Untermannigfaltigkeit von Jq (X , U) auf:
S = {(x , u (q) ) | Fk (x, u (q) ) = 0, k = 1, . . . , s}.
27
Kontakt(ko)distribution
Nicht jede Abbildung ϕ : X → Jq (X , U) ist eine Prolongation.
Dafür müssen gewisse Relationen gelten.
Die Kontaktdistribution Cq wird erzeugt von
Ci := ∂x i +
m
X
X
j
uµ+e
∂ j ,
i u
für i = 1, . . . , n,
µ
j=1 1≤|µ|<q
j
Cµ
:= ∂u j ,
für |µ| = q.
µ
Die Kontaktkodistribution C0q wird erzeugt von
j
ωµ
:=
j
duµ
n
X
j
−
uµ+ei dx i ,
i=1
für i = 1, . . . , m und 1 ≤ |µ| < q.
28
Kontakt(ko)distribution
C0q ist der Annullator von Cq .
Es ist ϕ = jq f für ein f : X → U genau dann, wenn für
ι : ϕ(X ) ֒→ Jq (X , U) gilt
j
ι∗ ωµ
= 0,
j = 1, . . . , m.
Also ist ϕ(X ) eine Integralmannigfaltigkeit von Cq .
29
Vessiot-Distribution
Eine Lösung f von S muss erfüllen:
jq f (X ) ⊆ S, d.h. Tjq f (X ) ⊆ TS.
jq f (X ) ist Integralmannigfaltigkeit von Cq , d.h. Tjq f (X ) ⊆ Cq .
Die Vessiot-Distribution ist definiert durch
dι(V(S)) := dι(TS) ∩ Cq ,
mit ι : S ֒→ Jq (X , U).
Es gilt ebenfalls
V(S) = (ι∗ C0q )0 .
Elemente von V(S) sind „infinitesimale Lösungen“ von S.
30
Implementierung
Aus einer Instanz von Dom::Manifold kann das q-te
Jetbündel erzeugt werden.
Methoden zur Berechnung von
Kontaktdistribution
Kontaktkodistribution
Vessiot-Distribution
sind in Dom::Manifold und Dom::SubManifold enthalten.
31
Gliederung
1
Objektorientierung in MuPAD
2
Mannigfaltigkeiten
3
Vektorfelder und Differentialformen
4
Differentialgleichungen
5
Beispiel: Die Monge-Ampère-Gleichung
32
Die Monge-Ampère-Gleichung
Die Monge-Ampère-Gleichung lautet
2
uxx uyy − uxy
= 0.
Unabhängige Variablen x, y. Abhängige Variable u.
Betrachte Jetbündel J2 (X , U).
Gleichung entspricht der impliziten Untermannigfaltigkeit
2
{(x, y, u, ux , uy , uxx , uxy , uyy ) ∈ J2 (X , U) | uxx uyy −uxy
= 0}.
33
Datenstrukturen für die Monge-Ampère-Gleichung
DV := Dom::DifferentialVariable([x,y], [u]);
DE := Dom::DifferentialExpression( DV );
MNF := Dom::Manifold;
SUB := Dom::SubManifold;
34
Datenstrukturen für die Kontaktdistribution
Erzeuge X und J2 (X , U):
X := MNF( [DV(x),DV(y)] );
Jet := MNF::jetBundle(X,2);
35
Kontaktdistribution
Berechne Kontaktdistribution von J2 (X , U):
MNF::contactDistribution( Jet );
∂x + ux ∂u + uxx ∂ux + uxy ∂uy
∂y + uy ∂u + uxy ∂ux + uyy ∂uy
∂uxx
∂uxy
∂uyy
36
Kontaktkodistribution
Berechne Kontaktkodistribution von J2 (X , U):
MNF::contactCodistribution( Jet );
du − ux dx − uy dy
dux − uxx dx − uxy dy
duy − uxy dx − uyy dy
37
Vessiot-Distribution der Monge-Ampère-Gleichung
Definiere die Differentialgleichung:
equation :=
DV(u([x,x]))*DV(u([y,y]))-DV(u([x,y]))ˆ2 = 0;
S := SUB(Jet, equation);
Berechne Vessiot-Distribution von S:
SUB::vessiotDistribution( S );
∂x + ux ∂u + uxx ∂ux + uxy ∂uy
∂y + uy ∂u + uxy ∂ux + uyy ∂uy
uxy
∂u
∂uxy + 2
uyy xx
uxx
∂u
∂uyy −
uyy xx
38
Zusammenfassung
Datenstrukturen für Mannigfaltigkeiten und Vektorfelder.
Methoden zur formalen Behandlung von
Differentialgleichungen.
In Zukunft:
Methoden weiter ausbauen.
Methoden für Distributionen.
Vorhandenes Symmetriepaket besser integrieren.
39
Zusammenfassung
Datenstrukturen für Mannigfaltigkeiten und Vektorfelder.
Methoden zur formalen Behandlung von
Differentialgleichungen.
In Zukunft:
Methoden weiter ausbauen.
Methoden für Distributionen.
Vorhandenes Symmetriepaket besser integrieren.
40
Zusammenfassung
Datenstrukturen für Mannigfaltigkeiten und Vektorfelder.
Methoden zur formalen Behandlung von
Differentialgleichungen.
In Zukunft:
Methoden weiter ausbauen.
Methoden für Distributionen.
Vorhandenes Symmetriepaket besser integrieren.
41
Zusammenfassung
Datenstrukturen für Mannigfaltigkeiten und Vektorfelder.
Methoden zur formalen Behandlung von
Differentialgleichungen.
In Zukunft:
Methoden weiter ausbauen.
Methoden für Distributionen.
Vorhandenes Symmetriepaket besser integrieren.