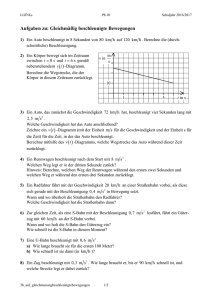
Gleichmäßige BESCHLEUNIGUNG - Freier Fall 1 von 2 PTS

Gleichmäßige BESCHLEUNIGUNG - Freier Fall
1. Eine Rakete beschleunigt nach dem Start konstant mit 40m/s². Welche Zeit würde die
Rakete theoretisch benötigen, um eine Geschwindigkeit zu erreichen, die der
Lichtgeschwindigkeit im Vakuum entspricht
v 3.108
1
t 
 7,5.10 6 s : 3600 : 24  86,8Tage  Jahr
a
40
4
2. Die Startbahn eines Flugplatzes ist 2,25km lang. Ein Verkehrsflugzeug benötigt zum
Abheben von der Startbahn die Geschwindigkeit v = 324km/h. Durch die Triebwerke
erhält das Flugzeug eine konstante Beschleunigung von 1,9m/s². Reicht die Länge der
Startbahn?
v
v2
km
m
1
1 v 2 1 v 2 1.90 2
t   t2  2
324
 90
s  a.t 2  a 2 

 2131,5
a
h
s
2
2 a
2 a
2.1,9
a
3. Ein 48m langer Eisenbahnzug hält in einer Station. Anschließend fährt er mit einer
Beschleunigung von 0,9 m/s²an
a) Berechne die Endgeschwindigkeit v, die der Zug nach einer Zeitspanne von 10s erreicht
hat.
b) Vor dem Anfahren hielt die Zugspitze an der vorderen Bahnsteigkante. Hat der Zug
nach 10s den Bahnsteig vollständig verlassen?
a
0,9
v=a.t= 0,9.10= 9 m/s
s  t2 
100  45m ; Nein
2
2
4. Eine Rakete wird vom Start mit a= 40 m/s² gleichmäßig beschleunigt, bis sie in eine
kreisförmige Umlaufbahn um die Erde eintritt. Sie hat nun eine Endgeschwindigkeit von
8 km/s erreicht.
a) Wie lange dauert diese Beschleunigungsphase
b) Welchen Weg legt die Rakete in dieser Zeit zurück.
v 8000
1
40.200 2
t 
 200s  3 min 20s
s  at 2 
 800 000m  800km
a
40
2
2
5. Ein Auto beschleunigt von 0 auf 100 km/h (gleichmäßig) in 15s. Berechne
a) die Beschleunigung b) den zurückgelegten Weg.
v
100 m
m
a.t 2 1,85.15 2
a

 1,85 2
s

 208,3m
t 3,6.15 s
2
2
s
6. Ein Fahrzeug wird aus dem Stillstand mit 0,8 m/s² gleichmäßig beschleunigt. Wie lange
braucht es um eine Geschwindigkeit von 72 km/h zu erreichen. Welchen Weg legt es bis
dorthin zurück?
72 m
m
v 20
1
0,8 2
v
 20
t 
 25s
s  at 2 
.25  250m
3,6 s
s
a 0,8
2
2
PTS-Nlb
Techn. Sem, Fachrechnen
1 von 2
Gleichmäßige BESCHLEUNIGUNG - Freier Fall
2 von 2
7. Mit zwei Motorrädern wird ein Beschleunigungstest gemacht. Motorrad Nr. 1 erreicht
nach 10 s die Geschwindigkeit v = 100 km/h. Motorrad Nr. 2 braucht eine
Beschleunigungsstrecke von 100 m um auf die Endgeschwindigkeit von 100 km/h zu
kommen. Welches Motorrad erreicht die größten Beschleunigungswerte ?
8. Zeige: v 
s
2s
t
b) Ist dies nicht ein Widerspruch zu v 
1 2
2s
at  a  2
2
t
v  a.t 
2s
2s
.t 
2
t
t
s
?
t
b) Nein! Verschiedene Bewegungsformen
9. Zwei Sportwagen beschleunigen von 0 auf 100km/h in A: 5 Sekunden
B: 7 Sekunden
a) Berechne den Abstand der beiden Sportwagen nach 4 Sekunden?
b) In welcher Zeit erreicht A bei gleichbleibender Beschleunigung 130km/h?
10.
Der freie Fall: Jeder Körper beschleunigt zur Erde mit ca. a=9,81m/s²
a=g=Erdbeschleunigung
(ohne Luftwiderstand !)
Berechne:
PTS-Nlb
a) Die Geschwindigkeit nach 12m
b) Die zurückgelegte Strecke nach 5 Sekunden
c) Die Geschwindigkeit nach 5 Sekunden
d) Nach wie viel Meter erreicht ein Körper 100 km/h
Techn. Sem, Fachrechnen