FRAGEN ZU KAPITEL 23 1 Abb. 23-19 zeigt drei - Wiley-VCH
Werbung
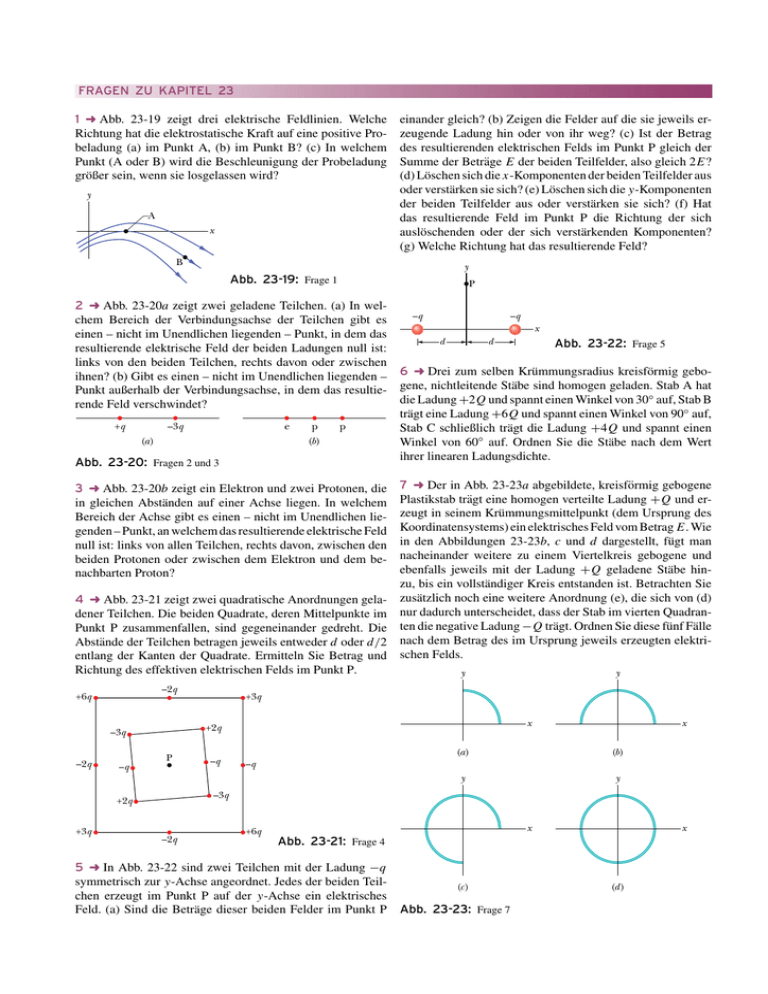
FRAGEN ZU KAPITEL 23 1 ➜ Abb. 23-19 zeigt drei elektrische Feldlinien. Welche Richtung hat die elektrostatische Kraft auf eine positive Probeladung (a) im Punkt A, (b) im Punkt B? (c) In welchem Punkt (A oder B) wird die Beschleunigung der Probeladung größer sein, wenn sie losgelassen wird? y A x B einander gleich? (b) Zeigen die Felder auf die sie jeweils erzeugende Ladung hin oder von ihr weg? (c) Ist der Betrag des resultierenden elektrischen Felds im Punkt P gleich der Summe der Beträge E der beiden Teilfelder, also gleich 2E? (d) Löschen sich die x-Komponenten der beiden Teilfelder aus oder verstärken sie sich? (e) Löschen sich die y-Komponenten der beiden Teilfelder aus oder verstärken sie sich? (f) Hat das resultierende Feld im Punkt P die Richtung der sich auslöschenden oder der sich verstärkenden Komponenten? (g) Welche Richtung hat das resultierende Feld? y Abb. 23-19: Frage 1 P 2 ➜ Abb. 23-20a zeigt zwei geladene Teilchen. (a) In wel–q –q chem Bereich der Verbindungsachse der Teilchen gibt es x einen – nicht im Unendlichen liegenden – Punkt, in dem das d d Abb. 23-22: Frage 5 resultierende elektrische Feld der beiden Ladungen null ist: links von den beiden Teilchen, rechts davon oder zwischen ihnen? (b) Gibt es einen – nicht im Unendlichen liegenden – 6 ➜ Drei zum selben Krümmungsradius kreisförmig geboPunkt außerhalb der Verbindungsachse, in dem das resultie- gene, nichtleitende Stäbe sind homogen geladen.◦ Stab A hat die Ladung +2Q und spannt einen Winkel von 30 auf, Stab B rende Feld verschwindet? trägt eine Ladung +6Q und spannt einen Winkel von 90◦ auf, +q –3q e p p Stab C schließlich trägt die Ladung +4Q und spannt einen (a) (b) Winkel von 60◦ auf. Ordnen Sie die Stäbe nach dem Wert ihrer linearen Ladungsdichte. Abb. 23-20: Fragen 2 und 3 7 ➜ Der in Abb. 23-23a abgebildete, kreisförmig gebogene Plastikstab trägt eine homogen verteilte Ladung +Q und erzeugt in seinem Krümmungsmittelpunkt (dem Ursprung des Koordinatensystems) ein elektrisches Feld vom Betrag E. Wie in den Abbildungen 23-23b, c und d dargestellt, fügt man nacheinander weitere zu einem Viertelkreis gebogene und ebenfalls jeweils mit der Ladung +Q geladene Stäbe hinzu, bis ein vollständiger Kreis entstanden ist. Betrachten Sie 4 ➜ Abb. 23-21 zeigt zwei quadratische Anordnungen gela- zusätzlich noch eine weitere Anordnung (e), die sich von (d) dener Teilchen. Die beiden Quadrate, deren Mittelpunkte im nur dadurch unterscheidet, dass der Stab im vierten QuadranPunkt P zusammenfallen, sind gegeneinander gedreht. Die ten die negative Ladung −Q trägt. Ordnen Sie diese fünf Fälle Abstände der Teilchen betragen jeweils entweder d oder d/2 nach dem Betrag des im Ursprung jeweils erzeugten elektrientlang der Kanten der Quadrate. Ermitteln Sie Betrag und schen Felds. Richtung des effektiven elektrischen Felds im Punkt P. y y 3 ➜ Abb. 23-20b zeigt ein Elektron und zwei Protonen, die in gleichen Abständen auf einer Achse liegen. In welchem Bereich der Achse gibt es einen – nicht im Unendlichen liegenden – Punkt, an welchem das resultierende elektrische Feld null ist: links von allen Teilchen, rechts davon, zwischen den beiden Protonen oder zwischen dem Elektron und dem benachbarten Proton? –2q +6q –q P –q x (a) (b) y y –q –3q +2q +3q x +2q –3q –2q +3q –2q +6q x x Abb. 23-21: Frage 4 5 ➜ In Abb. 23-22 sind zwei Teilchen mit der Ladung −q symmetrisch zur y-Achse angeordnet. Jedes der beiden Teil(c) chen erzeugt im Punkt P auf der y-Achse ein elektrisches Feld. (a) Sind die Beträge dieser beiden Felder im Punkt P Abb. 23-23: Frage 7 (d) Fragen zu Kapitel 23 8 ➜ Wie in Abb. 23-24 dargestellt bewegt sich ein Elektron e durch eine kleine Öffnung in der Platte A hindurch auf die Platte B zu. Ein homogenes elektrisches Feld im Raum zwischen den beiden Platten bremst das Elektron, ohne es abzulenken. (a) Welche Richtung hat das Feld? (b) Vier weitere Teilchen bewegen sich ebenfalls, wie in der Abbildung dargestellt, durch kleine Öffnungen der Platten in den Plattenzwischenraum hinein. Drei von ihnen tragen die Ladungen +q1 , +q2 und −q3 . Das vierte Teilchen, mit n bezeichnet, ist ein Neutron und verhält sich elektrisch neutral. Wie ändert sich die Teilchengeschwindigkeit in jedem dieser vier Fälle beim Eintritt in das elektrische Feld? e +q2 +q1 –q3 n A B Abb. 23-24: Frage 8 9 ➜ Abb. 23-25 zeigt die Flugbahn eines negativ geladenen Teilchens 1 durch einen rechteckigen Bereich, in dem ein homogenes elektrisches Feld herrscht: Das Teilchen wird in der Papierebene nach oben abgelenkt. (a) Ist das Feld nach oben, unten, links oder rechts gerichtet? (b) Drei weitere geladene Teilchen nähern sich wie dargestellt dem Feldbereich. Welche von ihnen werden nach oben, welche nach unten abgelenkt? 3 4 – + + – 2 1 Abb. 23-25: Frage 9 10 ➜ (a) Betrachten Sie noch einmal die Situation von Kontrollfrage 5: Ist die vom Feld am Dipol verrichtete Arbeit positiv, negativ oder null, wenn der Dipol von der Orientierung 1 in die Orientierung 2 gedreht wird? (b) Ist die vom Feld am Dipol verrichtete Arbeit größer, kleiner oder die gleiche wie in Frage (a), wenn man den Dipol aus der Orientierung 1 in die Orientierung 4 dreht? 11 ➜ Vier verschiedene Orientierungen eines elektrischen Dipols in einem elektrischen Feld haben die potenziellen Energien (1) −5U0 , (2) −7U0 , (3) 3U0 und (4) 5U0 , wobei U0 positiv sei. Ordnen Sie die vier Fälle nach (a) der Größe des Winkels zwischen dem Dipolmoment p und dem elektrischen Feld E, (b) dem Betrag des auf den Dipol wirkenden Drehmoments. 12 ➜ Läuft man an einem trockenen Tag über bestimmte Arten von Teppichen und greift dann nach einem metallenen Türgriff oder – um mehr Spaß zu haben – nach jemandes Nacken, so springt oft ein Funke über. Wie entsteht dieser Funke? (Man kann die Intensität – die Helligkeit und das Geräusch – der Entladung vergrößern, wenn man statt der Hand einen Finger oder einen scharfkantigen Metallgegenstand, beispielsweise einen Schlüssel, verwendet.)











