Planetenschleifen mit Geogebra
Werbung
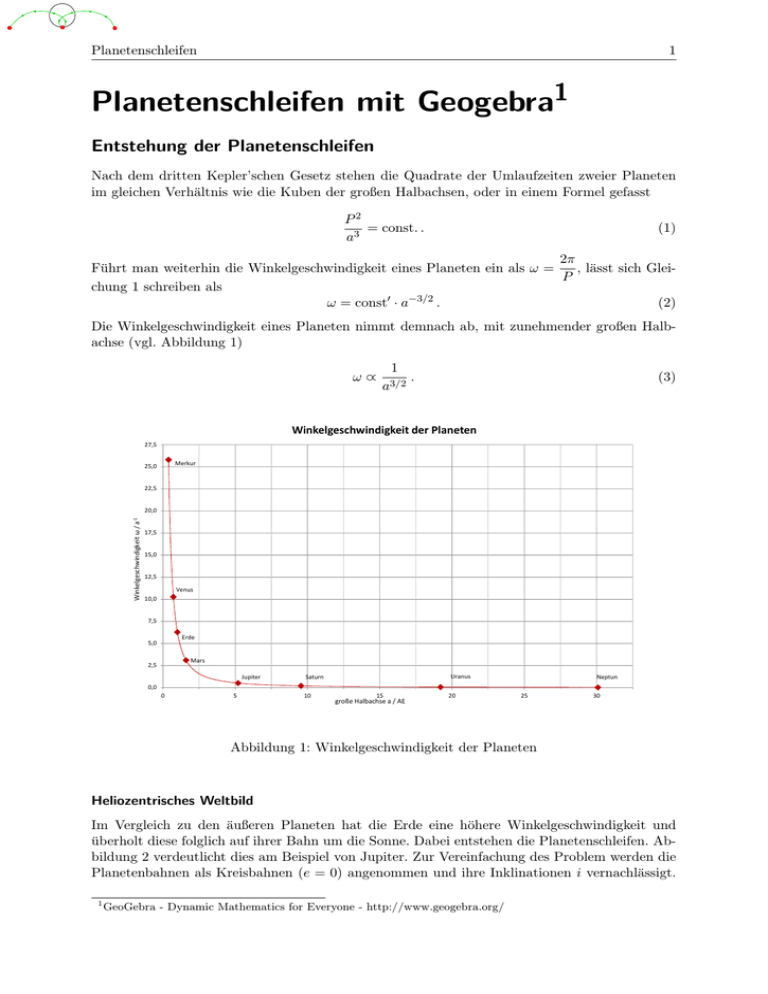
Planetenschleifen 1 Planetenschleifen mit Geogebra1 Entstehung der Planetenschleifen Nach dem dritten Kepler’schen Gesetz stehen die Quadrate der Umlaufzeiten zweier Planeten im gleichen Verhältnis wie die Kuben der großen Halbachsen, oder in einem Formel gefasst P2 = const. . a3 (1) 2π Führt man weiterhin die Winkelgeschwindigkeit eines Planeten ein als ω = , lässt sich GleiP chung 1 schreiben als ω = const0 · a−3/2 . (2) Die Winkelgeschwindigkeit eines Planeten nimmt demnach ab, mit zunehmender großen Halbachse (vgl. Abbildung 1) ω∝ 1 a3/2 . (3) Winkelgeschwindigkeit der Planeten 27,5 Merkur 25,0 22,5 Winkelgeschwindigkeit ω / a‐1 20,0 17,5 15,0 12,5 Venus 10,0 7,5 Erde 5,0 Mars 2,5 Jupiter Uranus Saturn Neptun 0,0 0 5 10 15 große Halbachse a / AE 20 25 30 Abbildung 1: Winkelgeschwindigkeit der Planeten Heliozentrisches Weltbild Im Vergleich zu den äußeren Planeten hat die Erde eine höhere Winkelgeschwindigkeit und überholt diese folglich auf ihrer Bahn um die Sonne. Dabei entstehen die Planetenschleifen. Abbildung 2 verdeutlicht dies am Beispiel von Jupiter. Zur Vereinfachung des Problem werden die Planetenbahnen als Kreisbahnen (e = 0) angenommen und ihre Inklinationen i vernachlässigt. 1 GeoGebra - Dynamic Mathematics for Everyone - http://www.geogebra.org/ Planetenschleifen 2 Am Himmel 6 5 7 4 13 13 7 3 6 12 12 8 5 11 4 9 10 3 9 11 2 10 1 2 1 Okt Jan 8 Jul Erdbahn Apr Jupiterbahn Abbildung 2: Entstehung der Planetenschleifen Weiterhin soll die Umlaufperiode P von Jupiter genau 12 Jahre betragen. Tabelle 1 zeigt die wahren Parameter der beiden Planeten. Die Abweichungen der vereinfachenden Annahmen sind nur gering und daher für den Einsatz im Unterricht annehmbar. Ein Jupiterumlauf dauert soa / AE P / Jahre e i /◦ Erde 1,00 1,00 0,017 0 Jupiter 5,20 11,86 0,048 1,31 Tabelle 1: Parameter Erde, Jupiter [1] mit 144 Monate. In Abbildung 2 sind sowohl auf der Erd-, als auch auf der Jupiterbahn die einzelnen Monate abgetragen. Im gezeigten Beispiel bewegt sich Jupiter in den Monaten Januar bis Juni (1-6) entgegen des Uhrzeigersinnes durch den Fixsternhimmel. In den Monaten 7-10 verläuft seine Bewegung gegenläufig, im Uhrzeigersinn. Die Monate 11-13 werden wieder im Gegenuhrzeigersinn durchlaufen. Diesen Verlauf bezeichnet man als Planetenschleife. Die beiden inneren Planeten Merkur und Venus haben hingegen höhere Winkelgeschwindigkeiten als die Erde. Sie überholen diese auf ihrer Bahn um die Sonne und erzeugen so ebenfalls Planetenschleifen mit der charakteristischen Phase der Rückläufigkeit des Planeten. Sowohl die Planetenschleifen der inneren, als auch der äußeren Planeten sind Projektionseffekte und im heliozentrischen Weltbild leicht durch die unterschiedlichen Winkelgeschwindigkeiten erklärbar. Planetenschleifen 3 Im geozentrischen Weltbild werden die Planetenschleifen dagegen durch die Überlagerung zweier Kreisbewegungen erklärt. Geozentrisches Weltbild Im geozentrischen Weltbild bewegt sich ein Planet auf einem Großkreis, dem sogenannten Deferenten um die Erde. Gleichzeitig bewegt sich der Planet auf einer zweiten Kreisbahn, dem Epizykel (vgl. Abbildung 3). Für die äußeren Planeten entspricht der Radius des Deferenten der REpi Deferent Epizykel RDef Erde Jupiter Abbildung 3: Planetenschleifen im geozentrischen Weltbild großen Halbachse des Planeten. Ein Umlauf des Epizykels dauert dabei gerade so lange wie die siderische Umlaufperiode des Planeten im heliozentrischen Weltbild. Der Radius des Epizykels entspricht der großen Halbachse der Erde und der Umlauf des Planeten auf dem Epizykel dauert ein Jahr. Bei inneren Planeten beträgt der Radius des Deferenten eine astronomische Einheit und die Umlaufzeit beträgt ein Jahr. Der Planet kreist dann auf dem Epizykel, dessen Radius der großen Halbachse des Planeten im heliozentrischen Weltbild entspricht. Die Umlaufdauer entspricht der siderischen Periode des Planeten. Tabelle 2 fasst die wichtigen Größen zusammen. Innere Planeten Äußere Planeten RDef 1 AE aP lanet PDef 1a Psid,P lanet REpi aP lanet 1 AE PEpi Psid,P lanet 1a Tabelle 2: Deferent und Epizykel im geozentrischen Weltbild [2] Planetenschleifen 4 Umsetzung in Geogebra Die Umsetzung wird hier am Beispiel von Jupiter beschrieben. Für alle anderen Planeten gelten die gleichen Formel. Die Umlaufzeiten und Radien der Bahnen müssen dann entsprechend angepasst werden. In Geogebra soll ein Skalenteil einer astronomischen Einheit entsprechen. Heliozentrisches Weltbild Die Erd- und Jupiterbahn sind konzentrische Kreise mit den Radien RE = 1 und RJup = 5, 2 um den gemeinsamen Mittelpunkt (0, 0) in welchem die Sonne sitzt. Der Fixsternhimmel wird als Kreis mit dem Radius RFix = 25, ebenfalls zentriert um die Sonne gewählt. Die Position der Erde wird durch den Vektor ~rE und die von Jupiter durch ~rJup beschrieben (vgl. Abbildung 4) Sic ht y/AE lin ie 5 4 Jupiter yJup,helio 3 2 rJup 1 Erde rE 1 2 3 4 5 x/AE xJup,helio Sonne Abbildung 4: Positionen der Planeten im heliozentrischen Weltbild ~rE = xE yE =1· cos(ϕE ) sin(ϕE ) , ~rJup = xJup yJup = 5, 2 · cos(ϕJup ) sin(ϕJup ) . (4) Die Winkel ϕE und ϕJup hängen von der Zeit ab und ergeben sich aus der Umlaufperiode der Planeten zu 2·π 2·π · M und ϕJup = ·M, (5) 12 144 M steht für die Anzahl der vergangenen Monate. Für die Erde ergibt sich ein voller Umlauf nach 12 Monaten und für Jupiter nach 144. Für die Anzahl der vergangenen Monate M wird ein Schieberegler im Bereich 0 ≤ M ≤ 144 hinzugefügt. Für die Projektion von Jupiter an den Fixsternhimmel fügt man einen Strahl durch zwei Punk” te“, beginnend im Punkt der Erde, weiter über den Punkt für Jupiter ein. Mit Hilfe des Werkzeugs Schneide zwei Objekte“ wird die Projektion, der Schnittpunkt zwischen Strahl und Fix” sternhimmel durch einen Punkt markiert. Zur Veranschaulichung wird in Geogebra eine Animation gestartet, welche die Anzahl der Monate in Schritten von 0,05 Monaten zwischen 0 Monaten und 144 Monaten variiert. Die Schleifenbewegung wird dann deutlich sichtbar. ϕE = Planetenschleifen 5 Geozentrisches Weltbild Im geozentrischen Weltbild setzt man zuerst einen Punkt für die Erde in den Koordinatenursprung, fügt einen Kreis für den Deferenten mit dem Radius RDef = RJup und einen mit dem Radius RFix = 25 hinzu; beide um den Mittelpunkt (0, 0). Der Mittelpunkt des Epizykelkreises läuft mit der siderischen Umlaufperiode von Jupiter auf dem Deferenten um. Dieser Punkt hat demnach dieselben Koordinaten wir Jupiter im heliozentrischen Weltbild. Man füge diesen Mittelpunkt und einen zugehörigen Kreis mit dem Radius REpi = 1 ein. Für den Planeten Jupiter fügt man nun einen Punkt auf dem Epizykel hinzu, dessen Koordinaten (xJup,geo , yJup,geo ) aus der Summe der beiden Kreisbewegungen bestehen 2·π 2·π xJup,geo = RDef · cos ·M + REpi · cos ·M 144 12 und ie 2·π 2·π yJup,geo = RDef · sin ·M + REpi · sin ·M . 144 12 yEpi Sic ht lin y/AE 5 yJup,geo 4 Jupiter Epizykel 3 yDef Deferent 2 1 1 2 3 4 xJup,geo Erde xDef 5 x/AE xEpi Abbildung 5: Positionen der Planeten im geozentrischen Weltbild Der Umlauf auf dem Epizykelkreis hat die Periodendauer PEpi = 12 Monate. Abschließend fügt man auch hier einen Strahl durch zwei Punkte zwischen Erde und Jupiter ein sowie den Schnittpunkt, welcher die Projektion an den Fixsternhimmel anzeigt. Nach Rechtsklick auf den Planeten kann die Eigenschaft Spur ein“ ausgewählt werden. ” Literatur [1] H. Karttunen: Astronomie - Eine Einführung; Springer-Verlag; 1990 [2] A. Unsöld, B. Baschek: Der neue Kosmos; 7. Auflage; Springer-Verlag; 2005