Aufgaben_Kreisbewegung_1

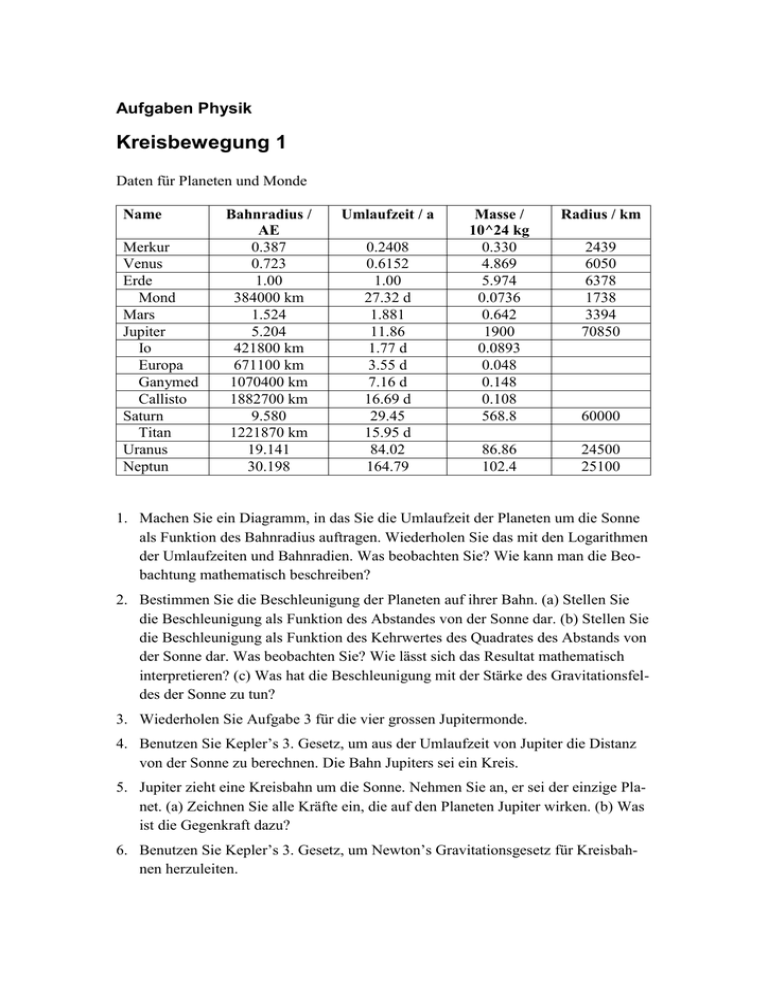
Aufgaben Physik
Kreisbewegung 1
Daten für Planeten und Monde
Name
Merkur
Venus
Erde
Mond
Mars
Jupiter
Io
Europa
Ganymed
Callisto
Saturn
Titan
Uranus
Neptun
Bahnradius /
AE
0.387
0.723
1.00
384000 km
1.524
5.204
421800 km
671100 km
1070400 km
1882700 km
9.580
1221870 km
19.141
30.198
Umlaufzeit / a
0.2408
0.6152
1.00
27.32 d
1.881
11.86
1.77 d
3.55 d
7.16 d
16.69 d
29.45
15.95 d
84.02
164.79
Masse /
10^24 kg
0.330
4.869
5.974
0.0736
0.642
1900
0.0893
0.048
0.148
0.108
568.8
Radius / km
86.86
102.4
24500
25100
2439
6050
6378
1738
3394
70850
60000
1. Machen Sie ein Diagramm, in das Sie die Umlaufzeit der Planeten um die Sonne
als Funktion des Bahnradius auftragen. Wiederholen Sie das mit den Logarithmen
der Umlaufzeiten und Bahnradien. Was beobachten Sie? Wie kann man die Beobachtung mathematisch beschreiben?
2. Bestimmen Sie die Beschleunigung der Planeten auf ihrer Bahn. (a) Stellen Sie
die Beschleunigung als Funktion des Abstandes von der Sonne dar. (b) Stellen Sie
die Beschleunigung als Funktion des Kehrwertes des Quadrates des Abstands von
der Sonne dar. Was beobachten Sie? Wie lässt sich das Resultat mathematisch
interpretieren? (c) Was hat die Beschleunigung mit der Stärke des Gravitationsfeldes der Sonne zu tun?
3. Wiederholen Sie Aufgabe 3 für die vier grossen Jupitermonde.
4. Benutzen Sie Kepler’s 3. Gesetz, um aus der Umlaufzeit von Jupiter die Distanz
von der Sonne zu berechnen. Die Bahn Jupiters sei ein Kreis.
5. Jupiter zieht eine Kreisbahn um die Sonne. Nehmen Sie an, er sei der einzige Planet. (a) Zeichnen Sie alle Kräfte ein, die auf den Planeten Jupiter wirken. (b) Was
ist die Gegenkraft dazu?
6. Benutzen Sie Kepler’s 3. Gesetz, um Newton’s Gravitationsgesetz für Kreisbahnen herzuleiten.
7. Wie gross ist die Masse der Sonne? Nehmen Sie die Bewegung der Erde um die
Sonne, um diesen Wert zu Berechnen.
8. Bestimmen Sie die Masse des Planeten Jupiter.
9. Vergleichen Sie die Gravitationskräfte, die die Sonne und der Mond auf die Erde
ausüben.
10. Bestimmen Sie die Gravitationsfeldstärke an der Oberfläche der Erde und des
Mondes.
Lösungen
1. Im log-log Diagramm gibt es eine Gerade. Die Beziehung zwischen Distanz und
Umlaufzeit ist eine Potenzfunktion. 2. (a) a = v^2/r = (2πr/T)^2/r = 4π^2·r/T^2 (b) Es
gibt eine Gerade. Die Beschleunigung ist umgekehrt proportional zum Abstand von
der Sonne. (c) Beschleunigung und Gravitationsfeldstärke müssen gleich sein. 5. (a)
Nur die (Gravitations)Kraft der Sonne auf Jupiter. (b) Die (Gravitations)Kraft von
Jupiter auf die Sonne; gleich und entgegengesetzt von (a). 7. m_Sonne = 2.0·10^30
kg. 9. FG_Sonne / FG_Mond = 178. (Warum ist dann die Gezeitenwirkung des
Mondes auf der Erde grösser als die der Sonne?)