C i - TU Ilmenau
Werbung
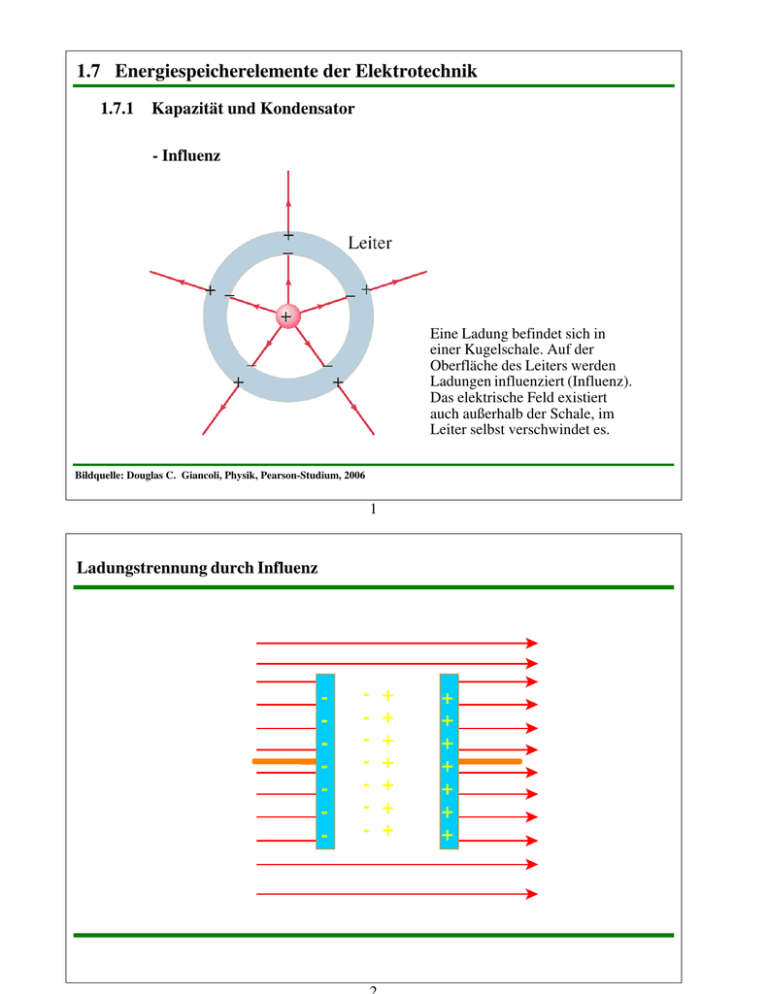
1.7 Energiespeicherelemente der Elektrotechnik 1.7.1 Kapazität und Kondensator - Influenz Eine Ladung befindet sich in einer Kugelschale. Auf der Oberfläche des Leiters werden Ladungen influenziert (Influenz). Das elektrische Feld existiert auch außerhalb der Schale, im Leiter selbst verschwindet es. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 1 Ladungstrennung durch Influenz - - + + + + + + + + + + + + + + Die elektrischen Feldlinien stehen senkrecht zur Leiteroberfläche. Warum ??? Hätte das elektrische Feld E an der Oberfläche eines Leiters eine parallel zur Oberfläche verlaufende Komponente, E||, so würde diese die Elektronen beschleunigen. Im statischen Fall (Ladungen ruhen), muss E|| null sein, also muss das elektrische Feld senkrecht zur Leiteroberfläche stehen. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 3 Die Abschirmwirkung geschlossener Leiterflächen: Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 Ein starkes elektrische Feld existiert in der Umgebung dieses „Faraday’schen Käfigs“. Es ist so stark, dass Elektronen aus den Atomen der Luft herausgeschlagen werden und Ladung zum (oder vom) Metallkäfig fließt. Doch die Person im Käfig ist davon nicht betroffen. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 5 Der “Ladungslöffel”: Ein geladener Leiter (Metallkugel) wird in eine isolierte Metalldose (guter Leiter) gesenkt, dessen Nettoladung null ist. Die geladene Kugel berührt die Dose und ihre gesamte Ladung fließt schnell zur Außenfläche der Dose. Wenn die Kugel anschließend wieder entfernt wird, stellt man fest, dass ihre Nettoladung null ist. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 van de Graff Generator Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 7 - Polarisation U + + + + + + + +Q + + + + + + + + + + + + + + ---- + + -----+ + ----- + + -----+ + ----- + + -- - -Q - - der ektrische Fluß Ψd Ψd Feld- bzw. Verschiebungslinien Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 9 - die ektrische Flußdichte D ∆Ψd, ∆Az Ψd Betrag und Einheit der elektrischen Flußdichte werden: [D] = 1As/m² Umgekehrt gilt: das elektrostatische Feld zweier ungleichnamig geladener Kugelelektroden 1 Daraus ergibt sich als Grundeigenschaft des elektrostatischen Feldes die Beobachtungstatsache: 0.5 0 -1 -0.5 0 0.5 1 1.5 2 11 Beispiel 1: ∫ D dA = Qumfaßt Der elektrische Fluss durch die Fläche A1 ist positiv. Der elektrische Fluss durch A2 ist negativ. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 ∫ D dA = Qumfaßt Beispiel 2: A Der Nettofluss durch die Fläche A ist gleich Null. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 13 Beispiel 3: ∫ D dA = Qumfaßt Der Nettofluss durch die Fläche A ist negativ. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 ∫ D dA = Qumfaßt Beispiel 4: Der elektrische Fluss durch die Fläche A1 ist positiv. Der elektrische Fluss durch A2 ist gleich Null. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 15 - der Zusammenhang zwischen elektrischer Flußdichte und Feldstärke für elektrisch lineare Werkstoffe gilt: D im Vakuum gilt die absolute Permittivität E ε 0 = 8,86 ⋅ 10−12 As Vm allgemein ist mit der relativen Permittivität: -Kapazität und Kondensator U Q +Q -Q U Dielektrikum Metallelektroden Q C U 17 die Proportionalitätskonstante wird als Kapazität bezeichnet. Bemessungsgleichung der Kapazität im homogenen Feld gilt: Q = Ψd = D A -Q +Q U = Ed A damit wird die Kapazität C= d Q DA εE A = = U Ed Ed U g - Permittivität 19 - Zusammenschaltung von Kondensatoren Reihenschaltung von Kondensatoren +Q C1 U1 C2 +Q +Q U2 Cn Q1 = Q2 = ⋯ = Qn = Q Un Uab CersR +Q Uab n Q 1 Q U ab = ∑ U i = ∑ = Q∑ = CersR i =1 i =1 Ci i = 1 Ci n n Parallelschaltung von Kondensatoren Uab Q1 Q2 Qn C1 C2 Cn U 1 = U 2 = ⋯ = U n = U ab n Q= n ∑Q = ∑U i i =1 n ab Ci =U ab ∑ Ci = U ab CersP i =1 i =1 CersP Uab 21 Der kapazitive Spannungsteiler U1 U2 Q Q 1 CersR C1 = 1 1 C2 + C1 + = C1 C2 C1 C2 C2 Uab Q = C1 U1 = C2 U 2 = CersR U ab CersR = C2 C1 C1 + C2 Technische Anwendungen - technische Kondensatoren Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 23 Kondensatoren mit fester Kapazität Plattenkondensator Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 Folienkondensator Kondensatoren mit variabler Kapazität Achse (isoliert) α Rotor Stator 25 Eine Taste einer Computertastatur. Beim Drücken der Taste verringert sich der Abstand der Kondensatorplatten, wodurch die Kapazität steigt. Dies wird von einem elektronischen Schaltkreis registriert. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 Koaxialkabel Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 27 Kondensatormikrofon Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 Energie im elektrostatischen Feld Q Q dWel=U dQ U U im linearen Fall ergibt sich Q = CU dQ = C dU 29 Kräfte auf Ladungen im elektrischen Feld Anwendungsbeispiele Beschleunigung von Elektronen (Kathodenstrahlröhre, Teilchenbeschleuniger) Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 Erzeugung gewollter Elektronenbahnen Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 31 Eine Kathodenstrahlröhre. Anstelle von elektrischen Ablenkplatten werden häufig magnetische Ablenkspulen verwendet. Die relative Lage der Bauteile wurde zur besseren Übersichtlichkeit übertrieben dargestellt. Bildquelle: Douglas C. Giancoli, Physik, Pearson-Studium, 2006 - der Verschiebungsstrom u(t) +Q(t) -Q(t) i(t) i(t) Ψd(t) Leitungsstrom im Nichtleiter gilt Q(t ) = C u( t ) 33 Zustandsänderungen an Kondensatoren ic(t) C uc(t) uc(t) t das Schaltgesetz: die Aufladung von Kondensatoren t=0 R i UQ Maschensatz: C U Q = R i + uC uC i= C duC dt lineare Differentialgleichung 1. Ordnung mit konstanten Koeffizienten UQ = R C duC + uC dt 35 t=0 R UQ = R C i UQ C duC + uC dt uC Abkürzung: RC = τ Lösungsmethode: -Trennung der Variablen UQ = τ duC + uC dt duC dt = − uC − U Q τ U Q dt = τ duC + uC dt − τ duC = uC dt − U Q dt duC dt = − ∫ uC − U Q ∫ τ t=0 R duC dt = − ∫ uC − U Q ∫ τ i UQ uC C ( ) ln uC − U Q = − t + ln K τ die allgemeine Lösung: uC = U Q + K e ln t − τ (u C )=− t − UQ τ K uC − U Q K = e − t τ 37 t=0 R i UQ uC = U Q + K e C − t τ uC − t τ uC = U Q (1 − e ) Anfangsbedingung: uC (0 − 0) = uC (0 + 0) = 0 = U Q + K e K = − UQ − 0 τ und für den Strom t UQ − t duC 1 − τ i= C = − U QC e (− ) = e τ dt τ R u(t) Kurvendiskussion: uC(t) t=0 R 0,7 UQ i 0,5 UQ UQ uC C t τ 1,2 0,7 i(t) − t uC = U Q (1 − e τ ) 0,5 UQ/R i= UQ R e − t 0,3 UQ/R τ i(t) t τ 1,2 0,7 39 - die Entladung von Kondensatoren t=0 uC i uC = U Q + K e R C uC = K e − − t τ t τ Anfangsbedingung: uC ( 0 − 0 ) = uC ( 0 + 0) = U 0 = K e K = U0 − 0 uC = U 0 e τ − t τ und für den Strom i = −C t duC 1 U −t − = − U 0C e τ ( − ) = 0 e τ dt τ R Kurvendiskussion: uC = U 0 e i= UQ R e − − t τ t τ i(t), uC(t) t τ 41