Exkurs Planetenbewegung
Werbung

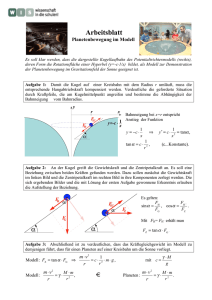
Exkurs F a M e F B1 Bahn e Kreis 0 Merkur 0,205 Venus 0,0067 Erde 0,017 Mars 0,094 Jupiter 0,049 Saturn 0,056 Uranus 0,046 Neptun 0,011 Pluto* 0,244 B2 *Pluto zählt seit August 2006 nicht mehr zu den Planeten. Planetenbewegung Die meisten Planeten unseres Sonnensystems bewegen sich auf Ellipsenbahnen, die kaum von einer Kreisbahn zu unterscheiden sind. Die Abweichung von einer Kreisbahn wird durch die numerische Exzentrizität e beschrieben; diese berechnet sich nach e = e/a, wobei e die Entfernung des Brennpunktes der Ellipse von ihrem Mittelpunkt und a ihre große Halbachse ist (O B1 ). Für die Bahn der Erde um die Sonne beträgt die numerische Exzentrizität 0,017, d. h., Brennpunkte und Mittelpunkt dieser Ellipse fallen fast zusammen. Nur bei Merkur und dem Kleinplaneten Pluto* hat man merkliche Ab­ weichungen von einer Kreisbahn (O B2 ). Die folgenden Berechnungen gehen von einer Kreisbahn aus. Die für die Bahn eines Planeten der Masse mP nötige Zentripetalkraft FZ wird von der wechselseitigen Gravitationskraft zwischen Planet und Sonne aufgebracht, d. h. die Kraft, die ein Planet durch die Masse der Sonne erfährt, zwingt ihn auf die Kreisbahn (O B3 ). 2 E FG = FZ FG B3 Aus der Bedingung, dass die Zentripetalkraft gleich der Gravitationskraft ist, ergibt sich: Dabei sind mP und mS die Massen von Planet und Sonne, z die Winkelgeschwindigkeit des Planeten, r der Radius der Kreisbahn und c die Gravitationskonstante. Aus dieser Gleichung kürzt sich die Planetenmasse heraus; ersetzt man die Winkelgeschwindigkeit durch 2 p/T, wobei T die Umlaufdauer des Planeten ist, so erhält man die Gleichung m 2 p 2 S _ ( _ T ) · r = c · r 2 und daraus durch Umformung Gravitationsfeld (2 p) 2 r m · m r 1 Das dritte Kepler’sche Gesetz lässt sich auf alle Systeme verallgemeinern, bei denen Körper bedingt durch die Gravitationskraft auf Bahnen um einen Zentralkörper kreisen. Beispielsweise wird die Erde als Zentralkörper vom Mond und inzwischen von einer Vielzahl künstlicher Satelliten umkreist (O B4 ). Für die Umlaufs­ dauer T und den Bahnradius r dieser Körper gilt in diesem System die Beziehung T _ __ 3 = c · m P S mP · z 2 · r = c · __ 2 B4 Fernseh-Satellit Da auf der rechten Seite nur Zahlen und Größen vorkommen, die unabhängig vom jeweiligen Planeten sind, ist dieser Ausdruck eine für alle Planeten gleiche Konstante. Ersetzt man den Bahnradius durch die große Halbachse a, so beschreibt diese Gleichung genau das dritte Kepler’sche Gesetz. Diese Konstante gilt allge­ mein für alle Objekte, die durch die von der Sonne ausgeübte Gravitationskraft auf eine Bahn um die Sonne gezwungen werden, wie z. B. auch die Asteroiden, das sind kleinere Himmelskörper, die sich hauptsächlich zwischen der Mars- und der Jupiterbahn be­wegen, oder auch die periodisch wiederkehrenden Kometen. 2 (2 p) 2 r S T = _ _ 3 c · m © Ernst Klett Verlag GmbH, Stuttgart, 2012 Diese Gleichung erhält man aus dem gleichen Ansatz wie für die Planetenbewegung um die Sonne; statt der Masse der Sonne steht jetzt die Masse der Erde mE in der Gleichung. Bestimmte Satelliten wie z. B. Fernseh- oder GPS-Satelliten (O B4 ) sollen sich immer über demselben Punkt der Erdoberfläche befinden. Ihre Umlaufsdauer muss dann genauso groß sein wie die Dauer einer Drehung der Erde um ihre Achse, nämlich ca. 24 h, das sind 86 400 Sekunden. (Tatsächlich beträgt die Dauer einer Erddrehung 23 h 56 min 4 s). Für einen solchen geostationären Satelliten ergibt sich dann eine Winkelgeschwindigkeit von 2 p z = ____ = 7,3 · 10 –5 _1s 86 400 s Aus der Gleichung 2 (2 p) 2 r E T _ __ 3 = c · m und der bekannten Masse der Erde (mE = 6,0 · 10 24 kg) kann dann der Bahnradius eines geostationären Satelliten errechnet werden. Man erhält r = 4,2 · 10 6 m = 42 000 km . Damit muss ein solcher Satellit in einer Höhe von etwa 36 000 km über der Erdoberfläche kreisen. Bildquellen: B4 dpa Picture-Alliance (UPI)