7.5 Kongruenzsatz Ssw

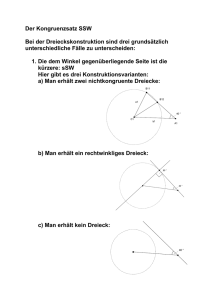
181
7.5 Kongruenzsatz Ssw
Interaktive Tafelbilder
7.5 Kongruenzsatz Ssw
■ Was haben die Dreiecke gemeinsam (Winkel, Seitenlängen)? Mit welchen drei Angaben
könnte man möglicherweise noch kongruente
Dreiecke konstruieren? ■
Blau markierter Winkel und zwei Seitenlängen, aber
nur jeweils zwei sind kongruent. Idee: Zwei Seitenlänge und ein nicht eingeschlossener Winkel, wenn er
der längeren Seite gegenüberliegt.
b
a
a
b
b
a
b
a
Einstieg:
Kongruenzsatz Ssw –
der Fall sSw:
Die Schülerinnen und
Schüler entdecken,
dass die Dreieckskonstruktion im Fall
sSw nicht eindeutig ist.
Ein Dreieck aus zwei Seiten und dem eingeschlossenen Winkel ist eindeutig konstruierbar
(Kongruenzsatz sws). Zu untersuchen ist, ob dasselbe gilt, wenn zu zwei Seiten ein anderer als
der eingeschlossene Winkel gegeben ist.
Beispiel 1: Konstruktion eines Dreiecks aus zwei Seiten und einem nicht eingeschlossenen Winkel
Von einem Dreieck ABC kennt man die Seitenlänge c = 4 cm und den Winkel α = 120°. Wie
lang muss die Seite a mindestens sein, damit überhaupt ein Dreieck entsteht? Untersuche
auch, ob diese Konstruktion eindeutig ist.
Lösung:
Erstelle eine Planfigur und kennzeichne die
gegebenen Größen farbig.
C
γ
b
Wenn du dynamische Geometrie-Software
verwendest, kannst du in kurzer Zeit viele
verschiedene Beispiele erzeugen.
Zeichne die Strecke c = 4 cm und beschrifte
die Eckpunkte mit A und B.
Trage den Winkel α = 120° in A ab, auf diesem freien Schenkel entsteht später die
Strecke b.
Zeichne um den Punkt B einen Kreis mit
beliebigem Radius. Auf diesem Kreis liegen
alle Punkte, die von B dieselbe Entfernung
a haben. Wähle den Radius so groß, dass
der Kreis den freien Schenkel schneidet.
Der Schnittpunkt ist C.
Ein Dreieck entsteht, wenn a größer als
4 cm ist, sonst entsteht kein Dreieck. Diese
Konstruktion ist eindeutig, da der Kreis den
freien Schenkel immer in genau einem
Punkt schneidet.
A
a
α
β
c
B
FunGeo
A
Strecke AB c=4
Winkel α=120°
α=120°
A c=4cm B
FunGeo
A
Strecke AB c=4
Winkel α=120°
A
B
Hinweis:
Es gibt ein zweites kongruentes Dreieck, das___
an der Spiegelachse AC
liegt.
FunGeo
A
Strecke AB c=4
Winkel α=120°
C
A
B
Aufgabe 1: Von einem Dreieck ABC kennt man die Seitenlänge a = 6 cm und den Winkel
β = 110°. Welche der folgenden Seitenlängen musst du wählen, damit ein Dreieck entsteht?
Konstruiere es mit 1 b = 4 cm; 2 b = 8 cm. Welches hat den üblichen Umlaufsinn? 8 cm