spannungs- und temperaturabhängige Widerstände
Werbung

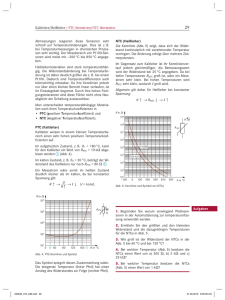
HSD Hochschule FB E I Düsseldorf Fachbereich Elektro- und Informationstechnik Bauelemente-Praktikum spannungs- und temperaturabhängige Widerstände VDR PTC Datum: NTC WS/SS 201.. Teilnehmer Name 1 2 U Gruppe: Matr.-Nr. T T 3 Testat Versuchsaufbau Nr.: verwendete Geräte: Von den Versuchsteilnehmern wird erwartet, daß sie sich vor dem Praktikumstermin mit der Versuchsthematik vertraut machen! Labor für elektronische Bauelemente und Schaltungen Prof. Dr. Lauffs · Dipl.-Ing. Hein Raum 5.2.46 · Tel.: 0211 / 4351-2320 Seite 1 Bauelemente-Praktikum, spannungs- und temperaturabhängige Widerstände 1. Grundlagen Elektrische Widerstände haben im Idealfall einen konstanten Wert R = const. und damit eine lineare Strom-Spannungs-Kennlinie I(U) = U/R mit konstanter Steigung ∆I/∆U = 1/R = const. Mitunter werden aber auch Widerstände benötigt, deren Wert mit der angelegten Spannung oder mit der Temperatur variiert. Der folgende Versuch behandelt drei dieser Widerstände: den spannungsabhängigen Widerstand, Kaltleiter sowie Heißleiter U 1.1 spannungsabhängiger Widerstand, Varistor, VDR (VoltageDependentResistor) Symbol: Eigentlich sind alle elektronischen Bauelemente mit nichtlinearer Strom-Spannungs-Kennlinie spannungsabhängige Widerstände – also z.B. auch Halbleiterdioden. Es ist jedoch üblich, als Varistor (abgekürzt: VDR) nur ein Bauelement zu bezeichnen, dessen progressiv ansteigende I(U)-Kennlinie punktsymmetrisch zum Ursprung verläuft - wie im folgenden Bild: I(U) Der Strom steigt ab einer bestimmten Ansprechspannung steil an. Sowohl der statische als auch der differentielle Widerstand sinken, wenn der Arbeitspunkt sich zu höheren Spannungen verschiebt. Im Bereich des steilen Stromanstieg läßt sich die Strom-Spannungs-Kennlinie recht gut durch die nebenstehende zugeschnittene Größengleichung annähern: Die Konstanten c und β sind den Datenblättern der Varistor-Hersteller zu entnehmen. (Mitunter sind sie allerdings anders bezeichnet.) 1 U / V = c ⋅ ( I / A )β mit c : Konstante 15 ...... 5000 U1 I1 = U2 I 2 β I• ∆I statischer Widerstand im Arbeitspunkt: β : Konstante 0,15 .... 0,4 U R• = • I• ∆U U• Daraus lassen sich die zugeschnittenen Größengleichungen für den statischen Widerstand R• sowie den differentiellen Widerstand r• in einem Arbeitspunkt der Kennlinie bei U• und I• herleiten: Aus Spannungs- und Strommessungen zweier Punkte im Steilanstieg der Kennlinie lassen sich außerdem die Konstanten c und β bestimmen. Mit den Meßwertpaaren U1 und I1 sowie U2 und I2 ergibt sich: differentieller Widerstand im Arbeitspunkt ∆U r• = ∆I U / V β I /A= c bzw. nach U aufgelöst : r• / Ω = R• / Ω = c⋅ U• / V = I• / A d ( I• / A ) = d c ⋅ ( I• / A )β = d ( I• / A ) ( I• / A )β = c ⋅ ( I• / A )β −1 I• / A β lg U1 I1 I1 U1 ⇒ lg = lg = β ⋅ lg g ⇒ β = I2 U2 I2 I2 lg I 1 d (U• / V ) U = c ⋅ β ⋅ ( I• / A )β −1 U 2 sowie c = U1 / V ( I1 / A ) β = U2 / V ( I 2 / A )β Die Herstellung von Varistoren ist einfach und erprobt: Siliziumkarbidkörnchen (ältere Typen) oder Zinkoxidkörnchen (typische Korngröße 20 µm) werden zu Keramikscheiben zusammengesintert, die mit Kontaktelektroden versehen werden. Die Korngrenzen bilden Potentialbarrieren, die bei ca. 3,5 V (für Zinkoxidkeramik) durchbrechen. Die Dicke der Varistorscheibe bestimmt die Anzahl der in Serie geschalteten Potentialbarrieren und damit die Ansprechspannung. Anwendungen sind Schutzschaltungen gegen hohe Spannungsspitzen, wie sie z. B. bei Blitzschlag oder Abschalten induktiver Lasten auftreten. Sie sind langsamer als die im nächsten Praktikumsversuch thematisierten Z-Dioden, können aber höhere Leistungen aufnehmen. Denn während in Z-Dioden die gesamte, in Wärme umgesetzte Verlustleistung in der sehr kleinen Sperrschicht anfällt, verteilt sich die Verlustleistung in Varistoren gleichmäßig auf das gesamte Volumen der Keramikscheibe. 1.2 temperaturabhängige Widerstände, Thermistoren Das Verständnis der Temperaturabhängigkeit des elektrischen Widerstandes erfordert zunächst die Wiederholung eines Kapitels der Werkstoffkunde-Vorlesung: Die elektrische Leitfähigkeit κ (kappa) eines Materials berechnet sich zu: κ = n·e·µn + p·e·µp Dabei ist n die Elektronendichte, p die Löcherdichte, µn bzw. µp sind die Beweglichkeiten der Elektronen bzw. Löcher und e ist die Elementarladung. In reinen Elektronenleitern (Metallen) entfällt der zweite Term der Gleichung. © Lauffs Seite 2 Bauelemente-Praktikum, spannungs- und temperaturabhängige Widerstände Grundsätzlich nimmt mit steigender Temperatur die Ladungsträgerbeweglichkeit µ ab weil zunehmende Gitterschwingungen die Ladungsträger in ihrer Beweglichkeit stärker behindern. Deshalb haben zunächst einmal alle Materialien einen positiven Temperaturkoeffizienten, d.h. ihr spezifischer Widerstand steigt mit der Temperatur. Dieser Effekt wird in undotierten oder nur schwach dotierten Halbleitern (Si, Ge, Metalloxid-Halbleiter-Keramiken) überdeckt durch eine exponentielle Zunahme der Ladungsträgerdichten n bzw. p mit steigender Temperatur, die so ausgeprägt ist, daß sie den zuerst beschriebenen Effekt vollständig überdecken kann. Durch die zusätzlichen freien Ladungsträger sinkt der Widerstand mit steigender Temperatur. Der Temperaturkoeffizient des Widerstandes wird negativ. Der Temperaturkoeffizient (TK oder auch α) des elektrischen Widerstandes ist definiert als TK = α = 1 dR ⋅ R dT [TK ] = [α ] = 1 K und meist nicht konstant sondern abhängig von der Temperatur, bei der er bestimmt wird. Nach dem Vorzeichen des Temperaturkoeffizienten unterscheidet man zwischen PTC (PositiveTemperatureCoefficient) und NTC (NegativeTemperatureCoefficient) Widerständen. PTC-Widerstände werden auch als Kaltleiter bezeichnet, weil sie im kalten Zustand besser leiten, NTC-Widerstände als Heißleiter, weil sie im heißen Zustand besser leiten. Zwei typische R(T)Kennlinien zeigt das folgende Diagramm: R(T) Ro 105 icient) PTC rature Coeff e p m e T e iv (Posit T Kaltleiter 104 103 NTC (Negative Temperatu re Coeffic ient) Heißleiter T 102 101 20 100 180 T/°C T 1.2.1 Kaltleiter, PTC (PositiveTemperatureCoefficient) Symbol: Der Heißwiderstand des Glühfadens einer normalen Glühbirne ist über zehnmal größer als der Kaltwiderstand. Man kann sich leicht davon überzeugen, wenn man mit einem Ohmmeter den Kaltwiderstand mißt und den Heißwiderstand aus der Betriebsspannung und der Leistung berechnet. Ein metallischer Glühfaden verhält sich also wie ein Kaltleiter und tatsächlich wurden glühende Eisendrahtwendel in einer Schutzgasatmosphäre (sog. Eisenwasserstoffwiderstände) früher als Kaltleiter verwendet. Heutige Kaltleiter sind allerdings fast ausschließlich polykristalline keramische Halbleiterbauelemente aus geeignet dotiertem Bariumtitanat oder Strontiumtitanat. Sie haben in einem engen Temperaturbereich einen deutlich steileren Anstieg des Widerstandes als metallische Kaltleiter. Auf den komplizierten Funktionseffekt soll hier nicht weiter eingegangen werden. Wenn die Temperatur eines Kaltleiters konstant gehalten wird, bleibt auch sein Widerstand konstant und er hat eine lineare I(U)-Kennlinie. Insofern ist es falsch, Kaltleiter grundsätzlich zu den nichtlinearen Bauelementen zu zählen. Wird an einen Kaltleiter aber ausreichend Spannung gelegt, erwärmt er sich infolge der ihm zugeführten Leistung P = U·I, sein Widerstand nimmt zu und trotz steigender Spannung kann der aufgenommene Strom wieder sinken (siehe dazu das Digramm auf der nächsten Seite). Dieser Effekt ist allerdings nur zu beobachten, wenn Spannung und Strom sich so langsam ändern, daß sich ein stationärer Zustand einstellt - d.h., daß sich die Kaltleiter-Temperatur auf einen konstanten Wert einpendelt. Für Spannungs- und Stromänderungen, die so schnell verlaufen, daß sich die Kaltleiter-Temperatur nicht ändern kann, zeigt sich eine dynamische, lineare I(U)-Kennlinie. Erst bei ausreichend langsamen U-I-Änderungen mißt man die sogenannte "stationäre", nichtlineare Kennlinie. Die dynamische Kennlinie kann nur mit schnellen Meßgeräten (z.B. einem Oszilloskop) gemessen werde. In diesem Praktikumsversuch soll die stationäre Kennlinie gemessen und aufgezeichnet werden. An den Meßpunkten der beispielhaften Kennlinie im folgenden Diagramm sind die aufgenommenen Leistungen sowie die Kaltleiter-Temperaturen notiert. Man beachte, daß Leistung und Temperatur mit der Spannung steigen, obwohl der Strom im rückläufigen Teil der Kennlinie fällt. © Lauffs Seite 3 Bauelemente-Praktikum, spannungs- und temperaturabhängige Widerstände I mA lineare dynamische Kennlinie (für TPTC = TU = const.) TU = 20°C lineare dynamische Kennlinie (für TPTC = 92°C = const.) 80°C 0,8 W 150 Umgebungstemperatur 92°C 0,96 W stationäre Kennlinie nichtlinear 100 98°C 1,04 W 50 0 101°C 1,08 W Kaltleiter 0 10 104°C TPTC = 110°C 1,12 W PPTC = 1,2 W 20 30 U/ V Weil die Leistung im rückläufigen Teil der Kennlinie näherungsweise konstant ist, zeigt dieser Teil mit I = P/U ~ 1/U angenähert den Verlauf einer Hyperbel. Interessant ist auch, daß der Kaltleiter im rückläufigen Teil seiner Kennlinie einen negativen differentiellen Widerstand haben muß, weil eine steigende Spannung hier einen sinkenden Strom zur Folge hat! Kaltleiter werden eingesetzt zur Temperaturmessung (wobei man hier meist metallische Kaltleiter z.B. aus Platin einsetzt), als thermischer Überlastungsschutz sowie zur Strombegrenzung. Ein in Serie zu einer Last geschalteter Kaltleiter verhält sich wie eine Sicherung, die den Strom allerdings nicht vollständig unterbricht, sondern auf einen Maximalwert begrenzt. Kaltleiter können zerstört werden, wenn ihnen ein großer Konstantstrom eingeprägt wird. Der Kaltleiter erwärmt sich, Widerstand, Spannung und Verlustleistung vergrößern sich, was eine noch stärkere Erwärmung zur Folge hat. Es kommt zu einer sog. thermischen Mitkopplung und der Kaltleiter wird durch Überhitzung zerstört. Bei Aufnahme der Meßwerte in diesem Praktikumsversuch darf der Kaltleiter deshalb nur mit eingeprägter Spannung betrieben werden. T 1.2.2 Heißleiter, NTC (NegativeTemperatureCoefficient) Symbol: Heißleiter sind Halbleiterbauelemente. Mit steigender Temperatur werden zusätzlichen freie Ladungsträger generiert, so daß die Leitfähigkeit des Halbleiters stark ansteigt und der Widerstand des Bauelementes sinkt. Im Prinzip ließen sich Heißleiter u.a. auch aus intrinsischem Silizium herstellen. Handelsübliche Heißleiter sind aber keramische, aus Metalloxiden gesinterte Bauelemente. Die Temperaturabhängigkeit des Heißleiterwiderstandes läßt sich recht gut durch folgende Formel annähern: R ( T ) = Ro ⋅ e 1 1 B⋅ − T To Ro = R ( T = To ) [T ] = [To ] = K [ B] = K Man beachte, daß die Temperatur hier unbedingt in der Einheit Kelvin einzusetzen ist! Die Parameter Ro, To sowie B können den Datenblättern der Hersteller entnommen werden. Ro ist der Bezugswiderstand bei der Bezugstemperatur To: meist 300 K bzw. ca. 25°C. B liegt bei handelsüblichen NTC-Widerständen zwischen 2500 K und 5000 K. Meßtechnisch ist B leicht aus zwei, bei T1 und T2 gemessenen Widerstandswerten R(T1) und R(T2) zu ermitteln: R ( T1 ) R ( T2 ) = e e 1 1 B⋅ − T1 To 1 1 B⋅ − T2 To =e 1 1 1 1 B⋅ − − B⋅ − T1 To T2 To B= Der Temperaturkoeffizient TK ist: 1 dR 1 d TK = ⋅ = ⋅ R dT R dT © Lauffs =e 1 1 B⋅ − T1 T2 ⇒ ln R ( T1 ) 1 1 = B⋅ − R ( T2 ) T1 T2 R ( T1 ) T1 ⋅ T2 R ( T1 ) 1 = ⋅ ln ⋅ ln 1 1 R ( T2 ) T2 − T1 R ( T2 ) − T1 T2 1 1 1 1 B⋅ − B⋅ − 1 B 1 B B T To T To = R ⋅ − 2 ⋅ Ro ⋅ e = R ⋅ − 2 ⋅ R = − 2 Ro ⋅ e T T T Seite 4 Bauelemente-Praktikum, spannungs- und temperaturabhängige Widerstände Wie die Berechnung zeigt, ist er immer negativ. I Für die I(U)-Kennlinie gelten ähnliche Überlegungen wie beim Kaltleiter: Solange die Temperatur eines Heißleiters konstant bleibt, hat er eine lineare I(U)-Kennlinie. Wird ihm (über eine einstellbare Stromquelle) ein ausreichend großer Strom zugeführt, erwärmt er sich, sein Widerstand sinkt und trotz steigenden Stroms kann die Spannung sinken. Im rückläufigen Teil seiner Kennlinie hat der Heißleiter einen negativen differentiellen Widerstand. Natürlich müssen - wie beim Kaltleiter - die I-U-Änderungen ausreichend langsam erfolgen, damit sich ein stationärer Zustand einstellen kann und man die stationäre Kennlinie aufzeichnen kann. Trägt man (wie in der Versuchsdurchführung) den Strom horizontal und die Spannung vertikal auf, ähnelt die stationäre Kennlinie der des Kaltleiters. stationäre Kennlinie Heißleiter Bei Betrachtung der stat. Kennlinie wird sofort klar, daß man an einen Heißleiter keine konstante Spannung anlegen darf, solange keine Maßnahme zur Strombegrenzung getroffen wurde: Es würde zu einer thermischen Mitkopplung kommen, der Strom würde auf sehr große Werte steigen und der Heißleiter würde durch Überhitzung zerstört. ie h Kennlin dynamisc U Ein in Serie zu einer elektrischen Last geschalteter Heißleiter begrenzt den Strom im Moment des Einschaltens durch seinen hohen Kaltwiderstand. Erst wenn er sich langsam erhitzt und seinen Widerstand reduziert hat, kann ein größerer Strom fließen. Heißleiter finden deshalb nicht nur Anwendung als Temperatursensoren, sondern auch zur Einschaltstrombegrenzung. 1.3 Literatur zu dem behandelten Themengebiet: K. Beuth: Elektronik 2 - Bauelemente, Vogel Buchverlag, Würzburg E. Böhmer: Elemente der angewandten Elektronik, Vieweg Verlag, Braunschweig/Wiesbaden F. Spickermann: Passive elektronische Bauelemente, J. Schlembach Fachverlag, Weil der Stadt M. Reisch: Elektronische Bauelemente, Springer-Verlag, Berlin, Heidelberg 2. Versuchsdurchführung Es sind die Kennlinien eines VDR sowie eines PTC- und eines NTC-Widerstandes aufzunehmen und graphisch darzustellen. Die Werte der I(U)-Kennlinie sind – stromrichtig – mit folgender Schaltung zu messen: stabilisiertes Netzgerät mit U einstellbarer Strombegrenzung R NTC PTC VDR Wiederholen Sie im Rahmen Ihrer Vorbereitung in diesem Zusammenhang, was unter strom- bzw. spannungsrichtiger Messung zu verstehen ist und wie sich die zugehörigen Meßschaltungen unterscheiden! Das stabilisierte Netzgerät verfügt über eine einstellbare Strombegrenzung für Ströme ≥ 10mA. Wenn die Strombegrenzung anspricht (rote LED leuchtet), arbeitet das Netzgerät als Konstantstromquelle. Dieser Konstantstrom-Modus ist hilfreich bei Messung der Ströme ≥ 10mA am VDR. Beim Heißleiter/NTC müssen Ströme ≥ 10mA im Konstantstrom-Modus eingeprägt werden, um eine Beschädigung des Heißleiters zu verhindern! Die Temperaturmessungen werden mit einem Thermoelement-Fühler durchgeführt. Fassen Sie den Fühler nicht direkt an der Meßspitze an, damit die Temperatur der Hand die Messung nicht verfälscht! Außerdem sollten Sie bei Temperaturmessungen in diesem Versuch immer eine Minute auf stabile Meßwerte warten, da der Versuchsaufbau thermisch träge ist und ausreichend Zeit benötigt, bis sich ein stationärer Zustand eingestellt hat. Die in die vorbereiteten Diagramme einzutragenden Meßpunkte sind unter Benutzung eines Kurvenlineals sauber miteinander zu verbinden, so daß ein geglätteter Kurvenverlauf sichtbar wird. Fehlerhafte Meßwerte (grobe Ausreißer) sind bei der Kurvenkonstruktion auszulassen. Gegebenenfalls interpolieren Sie ein geglättete Kurve, die sich den Meßwerten optimal annähert. © Lauffs Seite 5 Bauelemente-Praktikum, spannungs- und temperaturabhängige Widerstände 2.1 VDR – Spannungsabhängiger Widerstand: Messung der stationären I(U)-Kennlinie sowie der R(U)-Kennlinie U/V I/mA R/kΩ 8 Es sind die in der rechten Tabelle fehlenden Werte zu ermitteln. 0,01 Messen Sie vor allem bei den letzten Werten zügig, um die Erwärmung des VDR gering zu halten. Die statischen Widerstandswerte sollten erst nach Beendigung der Messungen ausgerechnet werden. 0,1 1 Im Rahmen der Versuchsausarbeitung sind die I(U)- sowie die R(U)-Kennlinie zu konstruieren. Zeichnen Sie dazu die gemessenen Punkte in die unten vorbereiteten Diagramme ein und legen Sie eine Kurve durch die Punkte. 5 10 25 I mA 25 20 15 10 5 0 8 10 12 14 16 18 20 22 U/V 24 8 10 12 14 16 18 20 22 U/V 24 10 M R Ω 1M 100 K 10 K 1K © Lauffs Seite 6 Bauelemente-Praktikum, spannungs- und temperaturabhängige Widerstände 2.2 PTC – Kaltleiter: Messung der stationären I(U)-Kennlinie sowie der R(T)-Kennlinie Stellen Sie die vorgegebenen Spannungen ein, warten Sie, bis sich die Stromanzeige stabilisiert hat und notieren Sie Ströme und Temperaturen. Ab dem zweiten Meßwert sollten Sie immer eine Minute auf eine stabile Anzeige warten. Im Rahmen der Versuchsausarbeitung ist die I(U)-Kennlinie zu konstruieren und an jedem zweiten Meßpunkt T sowie P zu notieren (wie im oberen Bild auf S.3). Schließlich ist noch die R(T)-Kennlinie zu konstruieren. U/V I/mA T/°C R/Ω P/mW U/V 1 9 3 10 5 12 6 14 7 16 8 20 I/mA T/°C R/Ω P/mW I 60 mA 50 40 30 20 10 0 R Ω 0 2 4 6 8 10 12 14 16 18 60 T/°C U/V 20 800 700 600 500 400 300 200 100 20 © Lauffs 30 40 50 70 Seite 7 Bauelemente-Praktikum, spannungs- und temperaturabhängige Widerstände 2.3 NTC – Heißleiter: Messung der stationären U(I)-Kennlinie sowie der R(T)-Kennlinie Stellen Sie die vorgegebenen Ströme ein, warten Sie, bis sich die Spannungsanzeige stabilisiert hat und notieren Sie Spannungen und Temperaturen. Ab dem zweiten Meßwert sollten Sie immer eine Minute auf eine stabile Anzeige warten. Im Rahmen der Versuchsausarbeitung ist die U(I)-Kennlinie zu konstruieren und an jedem zweiten Meßpunkt T sowie P zu notieren (wie im oberen Bild auf S.3). Schließlich ist noch die R(T)-Kennlinie zu konstruieren und der B-Parameter zu berechnen. I/mA Ab 10 mA ist das Netzgerät als Konstantstromquelle zu betreiben! U/V T/°C R/Ω P/mW I/mA 1 40 5 50 10 60 15 70 20 80 30 100 U V U/V T/°C R/Ω P/mW 12 10 8 6 4 2 0 0 10 20 30 40 50 60 70 80 90 I/mA 100 1000 R Ω 900 B =........... 800 Berechnung auf der Blattrückseite durchführen. Für R(T1) und R(T2) Anfangs- und Endwerte der Meßreihe wählen. 700 600 500 400 300 200 100 20 °C 293 K © Lauffs 30 °C 303 K 40 °C 313 K 50 °C 323 K 60 °C 333 K T 70 °C 343 K