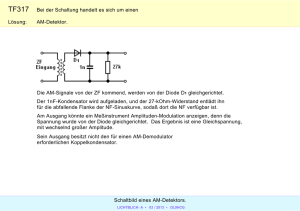
Reverse-Recovery-Verhalten bei verschiedenen Durchlassströmen

Technical Note PR-TN 2009/00487
Issued: 09/2009
Investigation and modelling of static and
dynamic behaviour if silicon-PSN- and
silicon-carbide-Schottky-diodes for low
currents
C. Neeb; P. Luerkens
Philips Research Europe
Unclassified

Koninklijke Philips Electronics N.V. 2009
PR-TN 2009/00487
Authors’ address
Unclassified
C. Neeb
[email protected]
P. Luerkens
[email protected]
© KONINKLIJKE PHILIPS ELECTRONICS NV 2009
All rights reserved. Reproduction or dissemination in whole or in part is prohibited without the
prior written consent of the copyright holder .
ii

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Title:
Investigation and modelling of static and dynamic behaviour if silicon-PSNand silicon-carbide-Schottky-diodes for low currents
Author(s):
C. Neeb; P. Luerkens
Reviewer(s):
IPS Facilities
Technical Note:
PR-TN 2009/00487
Additional
Numbers:
Subcategory:
Project:
Scalable Power Chain (2005-195)
Customer:
Keywords:
p-i-n diodes, power semiconductor diodes, Schottky barrier diodes, Schottky
diodes, behavioural modelling, silicon carbide, power diodes, device
modelling, high voltage diodes, high voltage generators, device simulation
Abstract:
High voltage generators for X-ray applications are moving to increasing
switching frequency. As a consequence switching losses, namely turn-on
losses, of high voltage diodes are becoming dominant. Data sheets of
preferred diodes do not contain relevant data in this respect, and simulation
models of common circuit simulators neglect these effects widely. In addition,
simulation speed of more detailed models is very poor. In this report,
commonly used diodes are investigated in their static and transient behaviour
and a time-efficient model is implemented in Orcad/Ppsice (transferrable to
LTSpice4, Simplorer under investigation) that allows the rapid simulation of
all relevant waveforms and losses with reasonable accuracy. A comparison of
the behaviour of silicon-PSN-diodes with upcoming silicon-carbide-Schottkydiodes in the 1-1.2kV range is given. (Report in German)
Conclusions:
Comparison of High-voltage Silicon-Carbide (SiC) Schottky diodes with high
voltage Silicon PSN diodes show an outstanding advantage in favor of the
SiC-diodes in high voltage rectifiers for x-ray systems, due to practical
absence of turn-on losses. A new mathematical model for calculation of
electrical behavior, both, for commonly used silicon diodes and also for
silicon carbide Schottky diodes allows quick design of high voltage circuits
and loss assessment by simulation.

Koninklijke Philips Electronics N.V. 2009
iii
Unclassified
PR-TN 2009/00487
Contents
Investigation and modelling of static and dynamic behaviour if
silicon-PSN- and silicon-carbide-Schottky-diodes for low currentsi
1.
Einleitung ..................................................................................................................9
2.
Theoretische Grundlagen ......................................................................................11
2.1. PN-Übergang...................................................................................................11
2.1.1. Struktur ................................................................................................11
2.1.2. Durchlassbelastung..............................................................................13
2.1.3. Sperrbelastung .....................................................................................15
2.1.4. Sperrfähigkeit ......................................................................................15
2.2. PSN-Anordnung ..............................................................................................16
2.2.1. Struktur ................................................................................................16
2.2.2. Durchlassbelastung..............................................................................16
2.2.3. Sperrbelastung .....................................................................................18
2.2.4. Sperrfähigkeit ......................................................................................19
2.3. Dynamisches Verhalten von Leistungsdioden ................................................20
2.3.1. Ausschaltvorgang ohne Sperrbelastung ..............................................20
2.3.2. Umschalten von Durchlass- auf Sperrbetrieb (Reverse-Recovery) ....20
2.3.3. Einschaltvorgang (Forward-Recovery) ...............................................22
3.
Diodenmodelle.........................................................................................................24
3.1. Grundlagen und Entwicklung der Modellbildung...........................................24
3.1.1. Makromodelle .....................................................................................24
3.1.2. Mikromodelle ......................................................................................25
3.2. Ausgewählte Ansätze ......................................................................................26
3.2.1. Methode der konzentrierten Ladungen ...............................................26
3.2.2. Charge-Control-Konzept .....................................................................30
3.2.3. Numerischer Ansatz von Vogler, Schröder.........................................32
3.2.4. Unified Diode Model ..........................................................................33
3.3. Schlussfolgerung .............................................................................................34
4.
Messschaltung .........................................................................................................35
4.1. Auswahl der Schaltung ...................................................................................35

Koninklijke Philips Electronics N.V. 2009
v
PR-TN 2009/00487
4.2.
4.3.
4.4.
4.5.
5.
Unclassified
4.1.1. Parametereinstellung ...........................................................................35
4.1.2. Stromsteilheit ......................................................................................36
4.1.3. Stabiles Leitverhalten ..........................................................................36
Messverfahren .................................................................................................36
Schaltungsentwurf ...........................................................................................37
4.3.1. Streuinduktivität ..................................................................................37
4.3.2. Strommessung .....................................................................................39
4.3.3. Anordnung der Messpunkte ................................................................39
Auswahl der Komponenten .............................................................................41
4.4.1. Induktivität ..........................................................................................41
4.4.2. MOSFET .............................................................................................41
Zwischenkreiskondensator ..............................................................................44
4.4.3. Shuntwiderstand ..................................................................................44
4.4.4. Platine ..................................................................................................44
Messtechnik ....................................................................................................44
4.5.1. Oszilloskop ..........................................................................................44
4.5.2. Tastköpfe .............................................................................................44
Messungen ...............................................................................................................46
5.1. Statische Messungen .......................................................................................47
5.2. Reverse-Recovery ...........................................................................................49
5.2.1. Variation des Durchlassstroms ............................................................49
5.2.2. Variation der Stromsteilheit ................................................................51
5.2.3. Variation der Temperatur ....................................................................53
5.3. Forward-Recovery...........................................................................................54
5.3.1. Variation des Durchlassstroms ............................................................54
5.3.2. Variation der Stromsteilheit ................................................................57
5.3.3. Variation der Temperatur ....................................................................57
5.4. Gesamtverluste ................................................................................................58
5.5. Sicherung der Messgenauigkeit ......................................................................59
5.5.1. Oszilloskop ..........................................................................................59
5.5.2. Einfluss der Schaltungsumgebung ......................................................61
6.
Simulationen ...........................................................................................................62
6.1. Modellansatz ...................................................................................................62
6.1.1. Modellierungstechnik ..........................................................................62
6.1.2. Grundstruktur ......................................................................................62
vi

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
6.2. Stationäres Verhalten ......................................................................................63
6.3. Transientes Verhalten......................................................................................64
6.3.1. Reverse-Recovery ...............................................................................65
6.3.2. Forward-Recovery ...............................................................................66
6.4. Parameterextraktion ........................................................................................68
6.4.1. Reverse-Recovery ...............................................................................68
6.4.2. Forward-Recovery ...............................................................................68
6.5. Vergleich von Simulationen und Messungen .................................................69
6.5.1. Reverse-Recovery ...............................................................................69
6.5.2. Forward-Recovery ...............................................................................71
6.6. Gültigkeit und Grenzen des Modells...............................................................72
7.
Zusammenfassung und Ausblick ..........................................................................74
A
Anhang.....................................................................................................................76
A.1 Messschaltung .................................................................................................76
A.1.1 Layout 76
A.1.2 Auswahl des MOSFETs ..................................................................................77
A.1.3 Synchronisierung der Tastköpfe .....................................................................77
A.1.4 Untersuchung auf parasitäre Kapazitäten und Induktivitäten .........................78
A.2 Simulationen ...................................................................................................79
A.2.1 Modellierungstechnik ......................................................................................79
A.2.2 Vergleich von Messungen und Simulationen .................................................80
Abkürzungsverzeichnis .................................................................................................84
Symbolverzeichnis .........................................................................................................85
Abbildungsverzeichnis ..................................................................................................87
Tabellenverzeichnis .......................................................................................................89
Literaturverzeichnis ......................................................................................................90

Koninklijke Philips Electronics N.V. 2009
vii
PR-TN 2009/00487
viii
Unclassified

Koninklijke Philips Electronics N.V. 2009
Unclassified
1.
PR-TN 2009/00487
Einleitung
Dioden sind wichtige Bauelemente in vielen leistungselektronischen Schaltungen. Bei
der Entwicklung dieser Schaltungen werden durch steigende Betriebsfrequenzen neben
den Durchlassverlusten auch die Schaltverluste in den Dioden zunehmend signifikant.
Betrachtet man das dynamische Verhalten von Siliziumdioden, so stößt man auf zwei
Effekte, durch die sich die Schaltverluste deutlich erhöhen: Erstens die Sperrverzögerung
(in der englischen Literatur als Reverse-Recovery bekannt) und zweitens die
Einschaltverzögerung (Forward-Recovery). Diese beiden Effekte werden in der
vorliegenden Arbeit beschrieben (Kapitel 2) und an drei Silizium-PSN-Dioden praktisch
untersucht. Dadurch wird die statische Charakterisierung anhand von Strom-SpannungsKennlinien auf transiente Vorgänge erweitert und so auch das dynamische Verhalten
erfasst.
Ein weit verbreitetes Hilfsmittel für den Schaltungsentwurf sind Schaltungssimulatoren
(z.B. PSpice). Sie ermöglichen es, eine Schaltung zu testen und zu analysieren, bevor sie
tatsächlich aufgebaut wird. Dadurch können Zeit und Kosten eingespart werden. Für
jedes verwendete Bauelement wird ein Modell eingesetzt, welches das reale Verhalten
möglichst genau wiedergeben soll. Eine höhere Genauigkeit kann dabei in der Regel nur
durch einen größeren Aufwand an Rechenzeit erreicht werden.
Zur Simulation von Dioden wird in PSpice gewöhnlich ein Modell verwendet, das für
Kleinsignal-Simulationen gedacht ist. Das dynamische Verhalten der Dioden wird daher
nur
im
Kleinsignalbereich
brauchbar
wiedergegeben.
Das
dynamische
Großsignalverhalten, welches bei der Simulation von leistungselektronischen
Schaltungen eine wichtige Rolle spielt, wird nicht vollständig wiedergegeben.
Deshalb sind in den letzten Jahrzehnten eine Vielzahl von Modellvorschlägen
veröffentlicht worden (Kapitel 3). Es ist jedoch noch nicht gelungen ein umfassendes
Diodenmodell zu entwickeln, das sich als neues Standardmodell durchgesetzt hat. In
üblichen Schaltungssimulatoren wird nach wie vor normalerweise ein unvollständiges
Diodenmodell eingesetzt, das für viele Anwendungen ausreichend ist und vor allem
kurze Rechenzeiten ermöglicht.
In dieser Arbeit soll ein gegenüber bekannten Modellen modifizierter Modellansatz
entwickelt und getestet werden (Kapitel 6). Hauptanforderungen an das neue Modell sind
die verbesserte Beschreibung des dynamischen Großsignalverhaltens sowie kurze
Rechenzeiten bei hinreichender Genauigkeit.
Das Modell soll für die Simulation von Hochspannungsdioden in einem
Röntgengenerator eingesetzt werden. Solche Generatoren arbeiten je nach Leistung
zwischen 60 und 300 kHz.
Zur Verifikation des simulierten Verhaltens werden Messungen an drei für die
Anwendung in Frage kommenden Silizium-PSN-Dioden durchgeführt (Kapitel 5). Dazu
wird eine Messschaltung entwickelt, die eine genaue statische und insbesondere
dynamische Charakterisierung der Dioden über einen möglichst weiten Arbeitsbereich
erlaubt (Kapitel 4).

Koninklijke Philips Electronics N.V. 2009
9
PR-TN 2009/00487
Unclassified
Es wird eine Betrachtung der Gültigkeit und Genauigkeit des Modells vorgenommen
(Kapitel 6). Abschließend erfolgt ein Vergleich der Silizium-PSN-Dioden mit
Siliziumkarbid(SiC)-Schottky-Dioden. Dabei wird insbesondere untersucht, wie sehr das
dynamische Verhalten durch den Einsatz von SiC verbessert werden kann und in
welchem Maße sich diese Verbesserung auf die Gesamtverluste der Dioden in der
praktischen Anwendung (Röntgengenerator) auswirkt.
10

Koninklijke Philips Electronics N.V. 2009
Unclassified
2.
PR-TN 2009/00487
Theoretische Grundlagen
Grundlegend für das statische und dynamische Verhalten von Dioden ist ihr Aufbau als
PN-Struktur. In diesem Kapitel wird ausgehend von einer kurzen Beschreibung des
einfachen PN-Übergangs zunächst die PSN-Struktur erläutert und anschließend auf die
hier auftretenden Reverse- und Forward-Recovery-Effekte eingegangen.
2.1.
PN-Übergang
2.1.1. Struktur
Ein PN-Übergang entsteht, wenn in einem Halbleiterkristall ein N- und ein P-leitendes
Gebiet aufeinandertreffen. Als Vereinfachung sei hier angenommen, dass die
Dotierungskonzentrationen nD+ und nA- in beiden Gebieten gleich groß und konstant bis
zur Stelle x = 0 seien. An dieser Stelle fallen beiden Konzentrationen schlagartig auf den
Wert Null ab. Die Akzeptoren bzw. Donatoren seien bei Raumtemperatur vollständig
ionisiert, sodass die Konzentration der Elektronen im N-Gebiet nn0 bzw. der
Defektelektronen im P-Gebiet pp0 jeweils gleich der Störstellenkonzentration sind
(Majoritätsträgerdichten). Aus der Bedingung [16]
nn0  pn0  ni2
(1)
bzw.
np0  p p0  ni2
(2)
für Halbleiter im thermischen Gleichgewicht folgt, dass auch eine
Elektronenkonzentration im P-Gebiet np0 bzw. eine Defektelektronenkonzentration im NGebiet pn0 vorhanden sein muss (Minoritätsträgerdichten). Typische Konzentrationswerte
(Abbildung 1) sind:
nn0  p p0  1014 cm-3
(3)
ni  1010 cm-3
(4)
np0  pn0  10 6 cm-3
(5)
Folglich kommt es an der Dotierungsgrenze x = 0 zu großen
Konzentrationsunterschieden. Diese verursachen Diffusionsströme der beiden
Ladungsträger vom Gebiet der hohen ins Gebiet der niedrigen Konzentration. Dadurch
wird der Konzentrationsgradient verringert. Die ionisierten Atomrümpfe bleiben zurück,
sodass eine Raumladungszone (RLZ) entsteht, die ein elektrisches Feld verursacht, das
vom N- zum P-Gebiet gerichtet ist. Dieses Feld bewirkt eine Kraft auf die beweglichen
Ladungsträger, die der Diffusionsrichtung gerade entgegengesetzt ist. Es stellt sich ein
Gleichgewichtszustand ein, in dem sich Diffusionsströme und Feldströme genau
kompensieren (Abbildung 1).

Koninklijke Philips Electronics N.V. 2009
11
PR-TN 2009/00487
Unclassified
Abbildung 1: PN-Übergang im thermischen Gleichgewicht [16]
Der Konzentrationsverlauf folgt dem Boltzmanngesetz [16]
 ( x)
n( x)  nn0  e
(6)
VT
Daraus kann mit Hilfe der Poissonschen Gleichung [16]
d ( x)
 ( x)

2
dx
  0
(7)
der Potentialverlauf  (x) und mit [16]
E ( x)  
d ( x)
dx
(8)
der Feldstärkeverlauf E (x) in der RLZ berechnet werden, wie in Abbildung 2 gezeigt ist.
Die Potentialdifferenz zwischen N- und P-Gebiet wird als Diffusionsspannung
bezeichnet.
12

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 2: Potential-, Feldstärke- und Raumladungsverlauf am PN-Übergang für
unterschiedliche Dotierungsprofile [16]
2.1.2. Durchlassbelastung
Die bisherigen Betrachtungen wurden unter der Voraussetzung des thermischen
Gleichgewichts ohne äußere Spannung vorgenommen. Nun wird am PN-Übergang von
außen eine positive Spannung angelegt; mit dem Pluspol am P-Gebiet und dem Minuspol
am N-Gebiet. Dadurch verringert sich die Diffusionsspannung. Der Potentialverlauf
ändert sich und damit auch der Konzentrationsverlauf. Die Majoritäts- und
Minoritätsträgerdichten an den Grenzen der RLZ werden entsprechend Abbildung 3
angehoben.

Koninklijke Philips Electronics N.V. 2009
13
PR-TN 2009/00487
Unclassified
Abbildung 3:Konzentrationsanhebung bei Durchlassbelastung[16]
Durch
die
Anhebung
der
Trägerkonzentration
werden
sowohl
die
Konzentrationsgradienten als auch die elektrische Feldstärke kleiner und somit werden
auch Diffusions- und Feldströme kleiner. Jedoch ist die Schwächung der Feldströme
stärker als die der Diffusionsströme, weswegen sich ein resultierender DefektelektronenTeilchenstrom vom P- in das N-Gebiet und ein Elektronen-Teilchenstrom vom N- in das
P-Gebiet ergeben. Defektelektronen aus dem P-Gebiet und Elektronen aus dem N-Gebiet
können quasi unbegrenzt nachgeliefert werden und somit stellt sich ein stationärer
Vorwärtsstrom ein.
In den Neutralgebieten fließt der Strom jeweils als Feldstrom der Majoritätsträger; ganz
links im P-Gebiet als reiner Defektelektronenstrom, ganz rechts im N-Gebiet als reiner
Elektronenstrom. Die Umwandlung des Elektronen- in einen Defektelektronenstrom
findet durch Rekombination statt und soll anhand der Darstellung in Abbildung 4
verdeutlicht werden. Elektronen treten in ein begrenztes Teilvolumen ein und
rekombinieren dort. Aus Neutralitätsgründen treten gleichzeitig auch Elektronen aus dem
Teilvolumen aus. Hierbei handelt es sich um solche, die unvollständige Paarbindungen
im Nachbarvolumen auffüllen. Das Austreten der Elektronen entspricht also dem
Eintreten von Defektelektronen. Alle Ladungsträger die innerhalb der PN-Struktur netto
kombinieren, müssen also in Form eines elektrischen Stromes zugeführt werden. Der
fließende Strom lässt sich somit durch das Integral über den Rekombinationsüberschuss
berechnen [16].
14

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 4: Stromübernahme durch Rekombination [16]

I D  e   R( x)dx

(9)
Bei der angelegten positiven Spannung steigt durch die Anhebung der
Trägerkonzentrationen der Rekombinationsüberschuss, da die Rekombinationsrate von
der Konzentration abhängt, die Paarerzeugungsrate jedoch nur von der Temperatur. Ein
steigender Rekombinationsüberschuss ist damit nach Gleichung (9) verbunden mit einem
wachsenden Strom.
Der Zusammenhang zwischen Strom und Spannung ergibt sich zu [16]:
I D (VD )  Is  (eVD VT  1)
( 10 )
2.1.3. Sperrbelastung
Beim Anlegen einer negativen Spannung addiert sich diese Spannung zur
Diffusionsspannung hinzu. Die dadurch erhöhte elektrische Feldstärke kann nur
aufgebaut werden durch eine Verbreiterung der RLZ. Die Konzentrationen der
Ladungsträger werden gegenüber dem thermischen Gleichgewicht verringert. Dadurch
ergibt sich ein negativer Rekombinationsüberschuss, durch den ein der Durchlassrichtung
entgegengesetzter Sperrstrom entsteht. Der negative Rekombinationsüberschuss kann
allerdings nicht beliebig gesteigert werden, da die Konzentrationswerte nur bis zum Wert
Null abgesenkt werden können. Der Sperrstrom ist also begrenzt (Sättigungscharakter)
und wird durch die Paarerzeugungsrate bestimmt, was zu einer starken
Temperaturabhängigkeit führt.
2.1.4. Sperrfähigkeit
Zwei Effekte begrenzen die Sperrfähigkeit einer PN-Struktur: Die Stoßionisation und der
Zener-Effekt. Aufgrund dieser beiden Effekte lässt sich eine kritische Feldstärke
definieren, oberhalb derer ein starker Sperrstromanstieg einsetzt, der rasch durch
thermische Verluste zur Zerstörung des Bauelements führen kann. Aus der kritischen
Feldstärke Ekrit lässt sich für eine gegebene PN-Struktur ein Wert für die maximale
Sperrfähigkeit VR max berechnen [16].

Koninklijke Philips Electronics N.V. 2009
15
PR-TN 2009/00487
Unclassified
2
VRmax  Ekrit

  0
e  nD 
( 11 )
Aus (11) wird deutlich, dass eine Erhöhung der Sperrfähigkeit bei vorgegebener
kritischer Feldstärke durch eine Verringerung der Dotierungskonzentration nD+ erreicht
werden kann (siehe auch Abbildung 2)
2.2.
PSN-Anordnung
2.2.1. Struktur
Eine hohe Sperrfähigkeit setzt nach Abschnitt 2.1.4 voraus, dass mindestens eine Seite
der PN-Struktur niedrig dotiert ist. Eine niedrige Dotierung bringt aber bei starker
Durchlassbelastung schlechte Durchlasseigenschaften mit sich, da in einiger Entfernung
von der PN-Grenze keine Trägeranhebung mehr auftritt und in diesem Bereich lediglich
die niedrige Dotierungsleitfähigkeit vorhanden ist.
Eine Verbesserung der Durchlasseigenschaften unter Beibehaltung der Sperrfähigkeit
lässt sich erreichen durch eine PSN-Anordnung, bei der sich zwischen zwei stark
dotierten Randgebieten ein schwach dotiertes Mittelgebiet befindet. Abbildung 5 zeigt
die Konzentrationsverteilung der beweglichen Ladungsträger in einer PN- und einer
PSN-Struktur bei starker Injektion (d.h. die Minoritätsträgerdichte übersteigt die
Dotierungskonzentration).
Abbildung 5: Konzentrationsverteilung bei starker Injektion [16]
Die erhöhte Trägerkonzentration im Mittelgebiet der PSN-Struktur wird dadurch erreicht,
dass bei Durchlassbelastung Ladungsträger aus den stark dotierten Randgebieten in das
Mittelgebiet einströmen.
2.2.2. Durchlassbelastung
Prinzipiell verhält sich die PSN-Struktur im Durchlassfall ähnlich wie die PN-Struktur.
An dieser Stelle soll deshalb lediglich auf die Konzentrationsverteilung in einer PSNStruktur bei starker Injektion genauer eingegangen werden. Für diese gilt die ambipolare
16

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Diffusionsgleichung (ADE) im stationären Fall, welche sich aus den
Stromdichtegleichungen der Elektronen und Löcher sowie den entsprechenden
Kontinuitätsgleichungen herleiten lässt [16]:
dn( x) 1
 2  n( x )  0
dx 2
La
( 12 )
mit der ambipolaren Diffusionslänge
La 
2n  p
n  p
 VT   HL
( 13 )
 HL bezeichnet die Lebensdauer der Ladungsträger bei starker Injektion (high-levelZustand) und ergibt sich aus der Summe [16]:
 HL   n   p
( 14 )
In Abbildung 6 sind Lösungen der ADE für verschiedene Mittelgebietsbreiten w bei
jeweils gleicher ambipolarer Diffusionslänge schematisch dargestellt. n0 stellt den
Mittelwert der Konzentration dar.
Abbildung 6: Schematische Darstellung von Lösungen der ambipolaren
Diffusionsgleichung
Der Zusammenhang zwischen Strom und Spannung lässt sich berechnen zu [16]:
 e  w  ni VRM
I D (VD )  
e
  HL
2VT
 VD
  e

2VT
( 15 )
Der Strom wächst hier im Gegensatz zu (10) nur mit eVD 2VT . Diese Gesetzmäßigkeit gilt
jedoch nur in einem kleinen Arbeitsbereich. Für höhere Ströme wächst die Spannung
überproportional, wie in Abbildung 7 dargestellt. Der zusätzliche Spannungsanstieg wird
verursacht durch eine wachsende Spannung VRM über dem Mittelgebiet, obwohl diese auf
den ersten Blick vom Strom unabhängig ist [16]:

Koninklijke Philips Electronics N.V. 2009
17
PR-TN 2009/00487
Unclassified
VRM
V
 T
2
w
  
 La 
2
( 16 )
Dieses Phänomen wird als Leitwertmodulation bezeichnet. Nach (13) hängt La jedoch
von den Beweglichkeiten der Ladungsträger ab, welche zu hohen Stromdichten
abnehmen. Damit nimmt La ab und nach (16) VRM zu.
Abbildung 7: Typische Kennlinie einer PSN-Diode [16]
2.2.3. Sperrbelastung
Bestimmend für das Sperrverhalten sind die Dotierungsverhältnisse am Übergang
zwischen stark P-dotiertem und schwach N-dotiertem Gebiet. Eine angelegte
Sperrspannung erzeugt an dieser Stelle eine RLZ, die sich aufgrund der wesentlich
18

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
niedrigeren Konzentration im N-Gebiet hauptsächlich in dieses ausbreitet. Der
Sperrstrom verhält sich hier ähnlich wie der Sperrstrom in einer PN-Struktur.
2.2.4. Sperrfähigkeit
Bedingt durch die geringe Dotierung im Mittelgebiet ist die Steigung des
Feldstärkeverlaufs relativ gering. Dadurch lässt sich ein größerer Potentialunterschied
erreichen, bevor die kritische Feldstärke erreicht wird. Die Sperrfähigkeit erhöht sich und
wird nicht nur durch die kritische Feldstärke begrenzt, sondern auch durch die Breite des
Mittelgebietes. Wenn sich die RLZ nämlich bis in das hochdotierte n-Gebiet ausbreitet,
erfolgt dort ein relativ abrupter Abbau der Feldstärke (s. Abbildung 8 links). Eine
Steigerung der Sperrspannung bei
gleicher kritischer Feldstärke und
Dotierungskonzentration ist durch eine Verbreiterung des Mittelgebietes möglich (s.
Abbildung 8 rechts).
Abbildung 8: Begrenzung der maximalen Sperrspannung einer PSN-Diode [16]

Koninklijke Philips Electronics N.V. 2009
19
PR-TN 2009/00487
2.3.
Unclassified
Dynamisches Verhalten von Leistungsdioden
2.3.1. Ausschaltvorgang ohne Sperrbelastung
Wird der Strom, der in Durchlassrichtung durch eine PSN-Struktur fließt, plötzlich
abgeschaltet, sind im Mittelgebiet noch Ladungsträger vorhanden, die nun nicht in Form
eines Stromes abfließen können. Der Abbau der Trägerkonzentration kann ausschließlich
durch einen Rekombinationsüberschuss erfolgen. Dabei ergibt sich ein exponentieller
Rückgang [16]:
n (t )  p(t )  n (0)  e
t
 HL
( 17 )
Der zeitliche und räumliche Verlauf der Trägerkonzentration ist in Abbildung 9
dargestellt.
Abbildung 9: Rückgang der Ladungsträgerkonzentration [16]
2.3.2. Umschalten von Durchlass- auf Sperrbetrieb (Reverse-Recovery)
Wird an eine in Durchlassrichtung belastete PSN-Struktur plötzlich eine Sperrspannung
angelegt, so kann nach dem Umschalten zunächst ein Rückstrom in Sperrrichtung
fließen. Dies ist möglich durch die noch vorhandene Überschwemmung des
Mittelgebietes mit Ladungsträgern, die durch die Sperrspannung ausgeräumt werden. Die
PSN-Struktur wirkt dadurch im ersten Moment wie ein Kurzschluss.
20

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Die Defektelektronen fließen nun in das stark dotierte P-Gebiet. Aus dem stark dotierten
N-Gebiet können praktisch keine Defektelektronen nachgeliefert werden. Entsprechendes
gilt für die Elektronen.
Typischerweise lässt sich der Verlauf des Rückstroms in drei Phasen unterteilen
(Abbildung 10).
Abbildung 10: Typischer Verlauf des Reverse-Recovery-Stroms
Phase 0 endet, wenn der Ausschaltvorgang der Diode beginnt. In Phase 1 nimmt der
Strom vom Wert des vorherigen Vorwärtsstroms linear ab bis zum Erreichen einer
Rückstromspitze Irr. In induktiven Schaltkreisen wird hier die Steigung im Wesentlichen
bestimmt durch die Kreisinduktivität Lpar und die angelegte Sperrspannung VR:
dI D VR

dt
Lpar
( 18 )
Der Rückgang der Konzentration verläuft bei angelegter Sperrspannung anders als beim
bloßen Ausschalten des Stromes. In Abbildung 9 ist zu sehen, dass die
Konzentrationsverteilung ohne äußere Spannung nach t   HL über das Mittelgebiet
ungefähr konstant verläuft. Bei angelegter Sperrspannung fällt die Konzentration an den
Übergängen zu den hochdotierten Randgebieten jedoch schneller ab, als in der Mitte des
Mittelgebietes. In dem Moment, in dem die Ladung an den Rändern auf einen Wert sehr
nahe bei Null zurückgegangen ist (Abbildung 11), beginnt Phase 2. Die PSN-Struktur
beginnt zu sperren. Die Rückstromspitze ist erreicht und der Strom geht allmählich auf
den Wert Null zurück, bis die verbleibenden Ladungsträger aus dem Mittelgebiet
ausgeräumt sind. Der Rückgang des Stroms nach Erreichen der Rückstromspitze kann

Koninklijke Philips Electronics N.V. 2009
21
PR-TN 2009/00487
Unclassified
sehr schnell erfolgen („aprupt recovery“, „snappy“) oder in Form eines langsamen
Abklingens („soft recovery“).
Abbildung 11: Konzentrationsverlauf beim Erreichen der Rückstromspitze
2.3.3. Einschaltvorgang (Forward-Recovery)
Wird in eine PSN-Struktur sprungartig ein Vorwärtsstrom eingeprägt, so muss die dazu
passende Ladungsträgerkonzentration im Mittelgebiet erst noch aufgebaut werden. Defektelektronen und Elektronen strömen aus den stark dotierten Randgebieten in das Mittelgebiet ein. Dieser Vorgang ist nicht trägheitslos, sondern es ergibt sich ein zeitlicher
Aufbau der Mittelgebietskonzentration wie ihn Abbildung 12 zeigt. Wieder tritt die
Lebensdauer  HL als Zeitkonstante auf.
Abbildung 12: Konzentrationsverlauf nach dem Einschalten [16]
Mit dem Aufbau der Mittelgebietskonzentration ist eine Verbesserung der Leitfähigkeit
verbunden. Im ersten Moment des Einschaltens wird die Durchlassfähigkeit noch durch
die Dotierungskonzentration bestimmt, der Widerstand des Mittelgebietes ist also noch
sehr hoch. Erst mit steigender Mittelgebietskonzentration nimmt dieser Widerstand ab,
bis die stationäre Durchlassfähigkeit erreicht ist.
22

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Der erhöhte Widerstand erzeugt bei sprungförmig eingeprägtem Strom Überspannungen,
die 1-2 Größenordnungen über der stationären Durchlassspannung liegen können. Dieses
Verhalten wird oftmals „induktiv“ genannt. Diese Bezeichnung ist jedoch irreführend.
Überlagert man einem konstanten Diodenvorwärtsstrom einen Wechselstrom, dessen
Amplitude klein gegenüber dem Konstantstrom ist (Kleinsignalmessung), so stellt man
fest, dass durch die Modulation des Widerstandes eine Phasenverschiebung zwischen
Strom und Spannung entsteht. Die Spannung eilt dem Strom voraus. Diese
Phasenverschiebung lässt sich in einem Kleinsignalersatzschaltbild durch eine
Induktivität darstellen. Falsch ist es aber nun, das Kleinsignalverhalten auf das
Großsignal zu übertragen und weiter von einem „induktiven“ Verhalten zu sprechen,
denn hier gibt es keine solche Phasenverschiebung. Die Nulldurchgänge von Strom und
Spannung erfolgen beim Einschalten zeitgleich.
Den meisten Schaltungsentwicklern sind die dynamischen Eigenschaften von Dioden,
wie die Ladungsspeicherung im Mittelgebiet und der Reverse-Recovery-Effekt,
wohlbekannt. Die Einschaltverzögerung (Forward-Recovery) wird aber im Allgemeinen
weniger beachtet. Da dieser Effekt lediglich im Nanosekundenbereich wirksam ist, haben
ihn viele Anwender und auch Hersteller von Dioden nicht berücksichtigt [20]. In der
letzten Zeit sind jedoch die Schaltfrequenzen in leistungselektronischen Anwendungen
insbesondere zur Verringerung der Größe von magnetischen Bauelementen so weit
gesteigert worden, dass die Verluste durch dieEinschaltverzögerung signifikant zu den
Gesamtverlusten der Dioden beitragen können.
Außerdem müssen die an der Diode bei steilen Einschaltflanken auftretenden
Überspannungen in den Schaltungsentwurf einbezogen werden, um andere Bauteile vor
Störungen oder gar Zerstörung zu schützen. Von daher ist eine genaue Spezifizierung des
Forward-Recovery-Verhaltens im Hinblick auf einen zuverlässigen Schaltungsentwurf
bei hohen Betriebsfrequenzen unabdingbar. In Datenblättern von Dioden findet man aber
gewöhnlich keine Angaben über das Einschaltverhalten [20].

Koninklijke Philips Electronics N.V. 2009
23
PR-TN 2009/00487
3.
Unclassified
Diodenmodelle
In diesem Kapitel wird ausgehend von einem kurzen Umriss der geschichtlichen
Entwicklung der Modellbildung zunächst eine Möglichkeit dargestellt, Diodenmodelle zu
klassifizieren. Anschließend werden verschiedene Modellansätze in ihren Grundzügen
dargestellt und kritisch bewertet.
3.1.
Grundlagen und Entwicklung der Modellbildung
Die Modellierung von Halbleiterbauelementen begann in den frühen 1950er Jahren, kurz
nachdem Van Roosbroeck (1950) die fundamentalen Halbleitergleichungen formuliert
hatte [7]. Diese bestehen aus dem nichtlinearen System von partiellen
Differentialgleichungen, das die Potentialverteilung, die Ladungsträgerkonzentration und
den Stromfluss in Halbleiterbauelementen beschreibt. In den 1990er Jahren wuchs durch
den Entwicklungsschub bei leistungselektronischen Schaltungen das Interesse an
Diodenmodellen beträchtlich an.
Das Reverse-Recovery-Phänomen wurde in den 1950er Jahren zuerst von Kingston
sowie Lax und Neustadter erforscht und über die Lösung der ambipolaren
Diffusionsgleichung (ADE) für die Minoritätsladungsträger beschrieben [5].
Die seitdem entstandenen Modellansätze lassen sich beispielsweise wie folgt
klassifizieren [18]:
Abbildung 13: Mögliche Klassifizierung von Modellansätzen
3.1.1. Makromodelle
Makromodelle reproduzieren empirisch das externe Verhalten der Bauteile. Im
Folgenden werden hierzu drei Möglichkeiten aufgezeigt.
Teilschaltungsmodelle
Es werden vorhandene Bausteine eines Simulationsprogramms so miteinander
verschaltet, dass der entstehende Schaltkreis sich so verhält, wie das zu simulierende
24

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Bauteil. Dazu wird z.B. von Bertha [2] das PSpice-Standarddiodenmodell mit
zusätzlichen Spannungs- und Stromquellen sowie einer LR-Kombination beschaltet.
Empirische Modelle
Es werden empirische Gleichungen formuliert, die zu einer Datenanpassung zwischen
Simulation und Messung führen. Der physikalische Hintergrund ist nebensächlich.
Solche Modelle haben oft eine Vielzahl von Parametern.
Tabellenmodelle
Tabellenmodelle basieren auf einer großen Anzahl von Bauteilmessungen, die im
gemessenen Bereich interpoliert werden können.
Makromodelle wurden vor Beginn der 1990er Jahre noch regelmäßig veröffentlicht.
Aufgrund ihrer Beschränkungen bezüglich Genauigkeit und Flexibilität werden seit den
1990er Jahren jedoch fast ausschließlich Mikromodelle verwendet [18].
3.1.2. Mikromodelle
Mikromodelle sind üblicherweise recheneffizienter, genauer und stehen in engerem
Bezug zur Bauteilstruktur. Sie lassen sich unterteilen in numerische, analytische und
hybride Modelle.
Numerische Modelle
Diese Modelle basieren auf der Lösung der halbleiterphysikalischen Gleichungen mittels
Finite-Elemente- oder Finite-Differenzen-Methode. Es lassen sich sehr genaue
Ergebnisse erzielen, jedoch nur, wenn die benötigten Eingabedaten (z.B. das
Dotierungsprofil) in ausreichender Genauigkeit bekannt sind. Deshalb ist bei dieser Art
von Modellen eine erfolgreiche Modellbildung stark von der Verfügbarkeit der Daten
abhängig.
Analytische Modelle
Analytische Modelle beruhen auf einem Satz von mathematischen Gleichungen, mit
denen das externe Verhalten des simulierten Bauteils berechnet werden kann ohne auf
Finite-Elemente-Methoden zurückgreifen zu müssen. Die Gleichungen stehen zwar in
Bezug zur Bauteilphysik, sind aber soweit vereinfacht, dass sie analytisch lösbar sind.
Analytische Modelle eignen sich besonders gut für die Simulation von
leistungselektronischen Schaltkreisen über eine große Anzahl von Schaltzyklen [18].
Hybride Modelle
Da bestimmte physikalische Phänomene in leistungselektronischen Bauteilen nur bedingt
realistisch mit analytischen Gleichungen berechenbar sind, gibt es noch diese dritte Art
von Mikromodellen als Kombination der beiden anderen. Hier wird die ADE, welche die
Vorgänge in den niedrig dotierten Gebieten beschreibt, mit Hilfe von numerischen
Algorithmen gelöst. Der Rest der Bauteilstruktur kann dann wiederum mit analytischen
Gleichungen beschrieben werden.

Koninklijke Philips Electronics N.V. 2009
25
PR-TN 2009/00487
3.2.
Unclassified
Ausgewählte Ansätze
Das Verhalten von Dioden mit kleinen Leistungen wird in Schaltungssimulatoren wie
z.B. PSpice zuverlässig wiedergegeben. Es liegt der Zustand der schwachen Injektion
vor, d.h. die
Minoritätsträgerkonzentration liegt weit unterhalb der
Dotierungskonzentration, und die überschüssigen Ladungsträger befinden sich
größtenteils in der Nähe der Sperrschicht. Die für solche Dioden verwendeten
Gleichungen sind in [1] beschrieben.
Halbleiterbauelemente, bei denen ein oder mehrere niedrig dotierte Gebiete von beiden
Seiten mit Ladungsträgern überschwemmt werden, sodass in einem weiten Bereich starke
Injektion vorliegt, können nicht mehr mit den verbreiteten Standardmodellen simuliert
werden [17]. Dies ist unter anderem der Fall bei den in dieser Arbeit untersuchten SiPSN-Dioden.
In diesem Abschnitt werden verschiedene aus der Literatur bekannte
Modellierungsansätze zur Simulation von Si-PSN-Dioden kurz vorgestellti. Auf die
Methode der konzentrierten Ladungen wird ausführlicher eingegangen, da das in dieser
Arbeit entwickelte Modell sich daran anlehnt.
3.2.1. Methode der konzentrierten Ladungen
Die Methode der konzentrierten Ladungen gehört nach dem Schema in Abbildung 13 zu
den analytischen Modellen und geht zurück auf Linvill [12]. Die verteilte Natur der
Ladungsträger im Mittelgebiet wird vereinfacht, indem angenommen wird, die Ladung
sei in mehreren Knoten konzentriert. Lauritzen und Ma haben diesen Ansatz in den
1990er Jahren aufgegriffen und weiterentwickelt [10], [13], [14]. Die von ihnen
angenommenen Ladungsknoten sind in Abbildung 14 dargestellt. Es wird von einem
symmetrischen Mittelgebiet ausgegangen. q m steht für die Ladung im Mittelgebiet und
stellt einen Ladungsspeicherknoten dar, qe steht für die an der Sperrschicht injizierte
Ladung und wird wie folgt aus der Sperrschichtspannung Ve berechnet [13]:
 Ve

qe  I s HL  e VT  1


( 19 )
Abbildung 14: Anordnung der Ladungsknoten
i
Die Bezeichnungen gleicher Größen in den unterschiedlichen Veröffentlichungen sind in dieser Arbeit
vereinheitlicht, um die Lesbarkeit und Vergleichbarkeit zu erhöhen.
26

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Die Verbindung der Ladungsknoten erfolgt über folgende sechs Gleichungen bzw.
Randbedingungen:

Stromdichtegleichung
ix   in x   ip x   in,Feld x   ip,Feld x   in.Diff x   ip,Diff x 
in,Feld x   e   n  nx   E x 
ip,Feld x   e   p  px   E x 
( 20 )
dnx 
dx
dp x 
ip.Diff  x   e  Dp 
dx
in.Diff  x   e  Dn 



Kontinuitätsgleichung der Ladungsträger
n
1 in
 R 
t
e x
p
1 ip
 R 
t
e x
( 21 )
0  nD x   px   nA x   nx 
( 22 )
Ladungsneutralität
Boltzmanngesetz
 x
nx   nn0  e


VT
( 23 )
d 2 x 
 x 

2
dx
  0
( 24 )
Poissonsche Gleichung
Kirchhoff'sche Maschen- und Knotenregeln
Die Kontinuitätsgleichung für die Ladungsträger qm im Mittelgebiet ist wie folgt
formuliert [13]:
0
dq m q m qe  q m


dt
 HL
Tm
( 25 )
Der erste Term in (25) steht für die zeitliche Änderung der im Mittelgebiet gespeicherten
Ladung, der zweite steht für die Rekombination der Ladungsträger mit der Lebensdauer
 HL und der dritte repräsentiert den Diffusionsstrom von der Sperrschicht ins
Mittelgebiet.

Koninklijke Philips Electronics N.V. 2009
27
PR-TN 2009/00487
Unclassified
Simulation des Reverse-Recovery-Verhaltens
Phase 1 des Reverse-Recovery-Stroms wird durch das Verhalten der
Schaltungsumgebung bestimmt. In leistungselektronischen Schaltungen tritt hier häufig
ein induktives Abschalten auf. Betrachtet man z.B. eine Tiefsetzsteller-Topologie
(Abbildung 15) im stationären Zustand (d.h. T schaltet mit gleichbleibendem Tastgrad
ein und aus), so fließt dort bei ausgeschaltetem Schalter T ein Strom durch die
Hauptinduktivität L und die Diode D. Wird T nun eingeschaltet, so erscheint D zunächst
als Kurzschluss (Abschnitt 2.3.2) und es wird in der Diode linear ein Rückstrom
aufgebaut, dessen Steilheit durch Vin und die Induktivität Ls bestimmt wird.
Abbildung 15: Topologie eines Tiefsetzstellers
Dieser eingeprägte Rückstrom wird gebildet durch ein Abfließen der überschüssigen
Ladungsträger im Mittelgebiet und kann so lange ansteigen, bis die
Ladungsträgerkonzentration qe einen Wert sehr nahe bei Null erreicht.
Für den Diodenstrom gilt nach [13] unter Vernachlässigung des Stromes aus der
Sperrschichtkapazität und eines Stromanteils, der durch die Rekombination in den stark
dotierten Randgebieten zustande kommt:
ID 
qe  q m
Tm
( 26 )
Ein Strom, wie ihn Abbildung 10 in Phase 1 zeigt, muss demnach eine
Konzentrationsverteilung erzwingen, wie sie in Abbildung 16 schematisch gezeigt ist.
Die Höhe des Stroms bestimmt den Konzentrationsgradienten.
28

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 16: Ladungsträgerabbau während Reverse-Recovery
Die Rückstromspitze Irr ist erreicht, wenn qe einen Wert sehr nahe bei Null erreicht. Erst
dann kann gemäß (19) die Sperrschichtspannung Ve negativ werden, da das Produkt aus
Is und  HL sehr klein ist. Die Diode beginnt zu sperren und die verbleibende Ladung im
Mittelgebiet nimmt nach (25) weiter ab. qe kann gleich Null gesetzt werden. Dann wird
(25) zu:
0
dq m q m 0  q m


dt
 HL
Tm
0
dq m q m q m


dt  HL Tm
0
 1
dq m
1 

 q m 

dt

T
m 
 HL
( 27 )
Die Lösung dieser Differentialgleichung lautet mit der Randbedingung qm 0  qm0 ,
wobei t  0 den Zeitpunkt beim Erreichen der Rückstromspitze bezeichnet:
qm t   qm0  e
mit
1
 eff


1
 HL
t
 eff

1
Tm
( 28 )
Der Strom in Phase 2 des Reverse-Recovery (Abbildung 10) lässt sich dann mit (26) und
(28) sowie der Bedingung qe  0 angeben:

Koninklijke Philips Electronics N.V. 2009
29
PR-TN 2009/00487
Unclassified
ID  
qm t 
Tm
t

q
 I D   m0  e  eff
Tm
( 29 )
Simulation des Forward-Recovery-Verhaltens
Um die auftretenden Überspannungen an der Diode bei schnellen Einschaltvorgängen zu
modellieren wird ein Serienwiderstand RM eingeführt, der den Bahnwiderstand des
Mittelgebietes repräsentiert und dessen Wert von der Ladung q m abhängt [13].
RM 
RM0
RM0
 qm  1
2  VT  TM
( 30 )
Steigt der Diodenstrom sprungförmig auf
ID 
qe  qm
 const
Tm
( 31 )
an, so steigt qm nach (25) exponentiell mit der Zeitkonstante  HL an. RM und damit auch
die Diodenspannung werden also allmählich kleiner.
Bewertung
Dieses Modell zeichnet sich durch seine Kompaktheit aus, ist jedoch nur für bestimmte
Leistungsdioden anwendbar [15]. In [10] und [13] sind keine Vergleichsmessungen zu
finden. Erst in einer späteren Veröffentlichung [14] werden je zwei Messungen des
Forward und Reverse-Recovery-Verhaltens mit den Simulationen verglichen. Die
Rückstromspitze Irr und die Einschaltspannungsüberhöhung VFRM werden exakt simuliert,
jedoch ist die Anstiegszeit der Diodenspannung von Null auf den Maximalwert in der
Simulation über 50 % länger als gemessen. Das Abklingen des Stromes nach Erreichen
der Rückstromspitze erfolgt in der Simulation etwas langsamer als gemessen.
Die Methode der konzentrierten Ladungen ist nicht nur für die Modellierung von
Leistungsdioden geeignet, sondern kann zur Modellierung von verschiedenen Typen von
Leistungshalbleitern verwendet werden [17]. Vorraussetzung dafür ist das Vorliegen von
starker Injektion in ausgedehnten Gebieten des Halbleitermaterials. Die verteilte Natur
der Ladungsträger kann dann durch an wenigen Punkten konzentrierte Ladungen
approximiert werden.
3.2.2. Charge-Control-Konzept
Auch das von Liang und Gosbell [11] beschriebene Modell gehört zu den analytischen
Modellen (s. Abbildung 13) und basiert auf der Kontinuitätsgleichung der Ladungsträger
im Mittelgebiet. Allerdings wird hier die Ladung nicht auf mehrere Knoten aufgeteilt,
sondern nur die Gesamtladung qm betrachtet.
30

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
dq m t  q m t 

  I D t 
dt
 HL
( 32 )
Reverse- und Forward-Recovery-Verhalten werden in separaten Untermodellen
modelliert.
Simulation des Reverse-Recovery-Verhaltens
Es wird eine Standarddiode verwendet, der eine gesteuerte Stromquelle parallel
geschaltet wird, um den Rückstrom zu modellieren. Anders als im Modell aus
Abschnitt 3.2.1 entsteht die charakteristische Stromform nicht direkt aus den
Modellgleichungen, sondern wird von einem Netzwerk aus passiven Bauelementen,
gesteuerten Quellen und Komparatoren erzeugt (s.~Abbildung 17).
Abbildung 17: Reverse-Recovery im Charge-Control-Konzept
Simulation des Forward-Recovery-Verhaltens
Es wird analog zur Reverse-Recovery-Modellierung eine gesteuerte Spannungsquelle zu
einer Standard-Diode in Reihe geschaltet. Die Spannungsquelle wird von einem
Netzwerk aus passiven Bauelementen und gesteuerten Quellen angesteuert. Dieses
Netzwerk enthält insbesondere eine RL-Kombination, welche das Abklingverhalten der
Überspannung bestimmt (s.~Abbildung 18).

Koninklijke Philips Electronics N.V. 2009
31
PR-TN 2009/00487
Unclassified
Abbildung 18: Forward-Recovery im Charge-Control-Konzept
Trotz der Verwendung von Teilschaltungen als Formulierungstechnik ist dieses Modell
nach dem Schema in Abbildung 13 kein Teilschaltungsmodell, da durch die
Teilschaltungen physikalische Gleichungen formuliert werden. Somit gehört das Modell
zu den Mikromodellen.
Bewertung
Durch die Realisierung von Forward- und Reverse-Recovery in separaten Teilmodellen
können diese Effekte auch nur getrennt simuliert werden. Eine Simulation über mehrere
Schaltzyklen ist nicht möglich. Es werden je drei Messungen des Forward- und ReverseRecovery Verhaltens präsentiert. Aufgrund der undeutlichen Darstellung der Messungen
ist jedoch nur ein grober Vergleich mit den Simulationen möglich.
3.2.3. Numerischer Ansatz von Vogler, Schröder
Mit der ADE lässt sich das Verhalten der Ladungsträger bei starker Injektion vollständig
beschreiben [19]:
p   p  ip 1 b
 D  
W
t x  x  e b  12 x

mit b  n Verhältnis der Beweglichk eiten
p
( 33 )
D  Ambipolare Diffusions konstante
W  Rekombinat ionsrate
Für diese nichtlineare partielle Differentialgleichung existiert keine geschlossene Lösung,
sodass Vogler und Schröder [19] ein Modell vorstellen, in welchem die ADE mit
numerischen Methoden gelöst wird.
32

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Simulation des Reverse-Recovery-Verhaltens
Der Abbau der Ladungsträgerkonzentration kann über die Lösung der ADE mit
entsprechenden von außen vorgegebenen Randbedingungen berechnet werden.
Simulation des Forward-Recovery-Verhaltens
Aufgrund der auf das Vorliegen von starker Injektion beschränkten Gültigkeit der ADE
kann das Modell erst ab dem Erreichen eines Schwellstromes angewandt werden. Für
kleinere Ströme wird zunächst mit der statischen Kennlinie gerechnet.
Bewertung
Die Implementierung des Modelles hält sich sehr genau an die physikalischen Vorgänge
im Halbleiter. Dadurch wird der Gebrauch von unphysikalischen Parametern wie mittlere
Ladungsträgerkonzentration und durchschnittliche Beweglichkeit vermieden. Es wird
somit einerseits eine hohe Simulationsgenauigkeit erreicht. Andererseits ist der
Rechenaufwand sehr hoch. Der Autor gibt für die Berechnung eines Umschaltvorgangs
eine Rechenzeit in der Größenordnung von wenigen Minuten anii. Das Modell ist
demnach praktisch nur für die Simulation kleiner Schaltkreise geeignet.
Es werden Simulationen der Forward- und Reverse-Recovery Verläufe bei je drei
verschiedenen Temperaturen mit dem vorgestellten Modell [19] und mit PISCES [23]
nebeneinander gestellt. Reale Messungen werden nicht veröffentlicht. Die
Übereinstimmung der Ergebnisse aus diesen beiden Berechnungsmethoden ist für das
Reverse-Recovery sehr genau. Der Anstieg der Einschaltspannungsüberhöhung ist jedoch
bei der Berechnung durch das Modell gegenüber der PISCES-Berechnung stark
verzögert (bis zu 100 %).
3.2.4. Unified Diode Model
Das von Mantooth und Duliere [15] beschriebene Modell versucht die Vorzüge einiger
Modelle zu vereinigen und durch zusätzliche Beiträge zu erweitern. So baut die
Implementierung der statischen Kennlinie auf einen Ansatz von Kraus [9] auf. Die
Vorwärtskennlinie wird mit vier exponentiellen Abhängigkeiten nachgebildet, die
Rückwärtskennlinie mit einer exponentiellen Abhängigkeit.
Simulation des Reverse-Recovery-Verhaltens
Die Realisierung des Reverse-Recovery basiert auf den Arbeiten von Lauritzen und Ma
[13] sowie Yang [22]. Die gespeicherte Ladung im Mittelgebiet wird gegliedert in einen
Anteil, der als Feldstrom ausgeräumt wird und einen Anteil, der durch Rekombination
und Diffusion abnimmt.
Simulation des Forward-Recovery-Verhaltens
Die Realisierung des Forward-Recovery geht zurück auf Lauritzen und Ma [13]. Der
entsprechende Widerstand RM wird hier definiert als:
ii

Wobei zu beachten ist, dass die Veröffentlichung aus dem Jahre 1992 stammt.
Koninklijke Philips Electronics N.V. 2009
33
PR-TN 2009/00487
Unclassified
w2
RM 
qm  n   p 
( 34 )
Bewertung
Der Autor erhebt den Anspruch, die besten Aspekte einiger anderer Modelle zu vereinen
und zu ergänzen. Das Modell sei experimentell an Zener-Dioden, Leistungsdioden mit
Stromtragfähigkeit von bis zu 200 A, Schottky-Dioden, Standarddioden aus der
Mikroelektronik sowie an Body-Dioden von Leistungs-Mosfets verifiziert worden. Es
werden je eine Messung zum statischen Verhalten (bei verschiedenen Temperaturen)
sowie Forward- und Reverse-Recovery gezeigt. Die Kurven werden direkt übereinander
gelegt, sodass sie leicht verglichen werden können. Die Übereinstimmung ist
hervorragennd. Da jedoch nur je ein Spezialfall präsentiert wird, ist nicht ersichtlich, ob
für andere Belastungsfälle eine ebenso gute Übereinstimmung erreicht wird. Das Modell
ist die Basis für alle Diodenmodelle in den Bauteilbibliotheken von Analogy geworden.
Das ist wohl der Grund dafür, dass die Modellgleichungen und deren Herleitung nicht
veröffentlicht worden sind. Darum ist es leider nicht wissenschaftlich verwertbar.
3.3.
Schlussfolgerung
Alle hier vorgestellten Diodenmodelle realisieren neben dem Reverse-Recovery auch den
Forward-Recovery-Effekt während sich viele andere Modelle auf das Reverse-RecoveryVerhalten beschränken. Den Modellen gemein ist außerdem, dass sie sich auf die
transienten Vorgänge konzentrieren und die Implementierung der statischen
Charakteristik relativ umständlich gelöst wird.
In dieser Arbeit soll ein Diodenmodell zur Schaltungsimulation über viele Schaltzyklen
entwickelt werden. Ein numerischer Ansatz wie von Vogler und Schröder
(Abschnitt 3.2.3) ist damit aufgrund des hohen Rechenaufwandes ausgeschlossen. Das
Charge-Control-Konzept von Liang und Gosbell (Abschnitt 3.2.2) ist nicht geeignet, da
Forward- und Reverse-Recovery in getrennten Untermodellen implementiert sind.
Mantooth und Duliere veröffentlichen keine Gleichungen zu ihrem Modell
(Abschnitt3.2.4). Daher kann auch dieses Modell hier keine Anwendung finden.
Somit ist die Methode der konzentrierten Ladungen (Abschnitt 3.2.1) für die gegebene
Aufgabenstellung am ehesten geeignet und das in Kapitel 6 entwickelte Modell lehnt sich
daran an.
34

Koninklijke Philips Electronics N.V. 2009
Unclassified
4.
PR-TN 2009/00487
Messschaltung
Das dynamische Verhalten der Dioden wurde mit der sog. Clamped-Inductive-Load
Testschaltung gemessen. Mit dieser Schaltung kann sowohl die Sperr- als auch die
Durchlassverzögerung gemessen werden. Den grundsätzlichen Aufbau zeigt
Abbildung 19.
Abbildung 19: Clamped-Inductive-Load Testschaltung
4.1.
Auswahl der Schaltung
Die im Folgenden aufgeführten Vorzüge waren ausschlaggebend für die Auswahl dieser
Schaltung für die vorliegende Messaufgabe.
4.1.1. Parametereinstellung
Laut Catt [3] müssen sich in einer Testschaltung zur Messung des Reverse-RecoveryEffektes die Parameter Vorwärtsstrom ID, Sperrspannung VR und Steigung des
Stromes dID/dt unabhängig voneinander einstellen lassen. Dies ist bei der von ihm [3]
behandelten und hier verwendeten Schaltung gewährleistet.
Der Vorwärtsstrom lässt sich gemäß
I D 
VDC
L  t1
( 35 )
über die Wahl der Eingangsspannung VDC, der Induktivität L sowie der

Koninklijke Philips Electronics N.V. 2009
35
PR-TN 2009/00487
Unclassified
Einschaltdauer t1 einstellen. Die Sperrspannung entspricht im Wesentlichen der
Eingangsspannung VDC. Die Steigung des Stroms kann sowohl beim Ein- als auch
Ausschalten der Diode über die Variation des Gatewiderstands eingestellt werden.
4.1.2. Stromsteilheit
Sowohl beim Ein- als auch beim Ausschalten der Diode lassen sich sehr hohe
Stromsteilheiten erreichen. Dabei ist die Stromsteilheit dID/dt lediglich durch die
Schaltgeschwindigkeit des Mosfets sowie durch die Streuinduktivität der Schaltung
begrenzt.
4.1.3. Stabiles Leitverhalten
Zwischen dem Ein- und Ausschalten der Diode muss für ausreichend lange Zeit ein
stabiler Strom fließen, damit die Diode ihre volle Leitfähigkeit erreicht bevor das
Ausschaltverhalten gemessen wird. Diese Anforderung wird von der hier verwendeten
Testschaltung erfüllt, da der Strom nach dem Einschalten der Diode durch die
Induktivität nahezu konstant gehalten wird.
4.2.
Messverfahren
Am Gate des Mosfets T wird ein Doppelpulssignal mit variablen Pulsbreiten angelegt.
Die Strom- und Spannungsverläufe sind in Abbildung 20 dargestellt. Während des ersten
Pulses (0 < t < t1) erfolgt in der Induktivität L ein linearer Stromaufbau gemäß
dI D VDC

.
dt
L
( 36 )
Die Diode befindet sich zunächst im sperrenden Zustand.
Während t1 < t < t2 sperrt T, der Strom IL wird in die Diode gezwungen und bleibt dann
näherungsweise konstant, solange bis die Diode ihre volle Leitfähigkeit erreicht hat.
Zum Zeitpunkt t2 wird T wieder leitend, die Diode geht in den Sperrbetrieb und der
Strom kommutiert aus der Diode zurück in T.
T wird bei t3 wieder ausgeschaltet, der Strom zirkuliert dann durch L und die Diode und
nimmt langsam, gemäß I D t   I D0  e
t
L
R
bis auf den Wert Null ab.
Die Messung des Forward-Recovery-Verhaltens erfolgt zum Zeitpunkt t1, die Messung
des Reverse-Recovery-Verhaltens zum Zeitpunkt t2.
36

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 20: Strom- und Spannungsverlauf während eines Messdurchlaufs
Catt [3] und Winterhalter [21] geben mehrere Beschränkungen der Testschaltung an.
Diese beziehen sich vor allem auf den Einfluss der Beschaltung auf die Messergebnisse.
Es wird jeweils eine alternative Testschaltung vorgeschlagen, die zu einer verbesserten
Qualität der Messergebnisse führen soll. Diese Schaltungen können jedoch nur zur
Messung des Ausschaltverhaltens verwendet werden und kommen somit für die
Untersuchungen in dieser Arbeit nicht in Frage.
4.3.
Schaltungsentwurf
4.3.1. Streuinduktivität
Ein entscheidender Aspekt beim Schaltungsentwurf ist die Minimierung der
Streuinduktivität. Dadurch sollen möglichst steile Stromflanken erreicht werden.
Während der Schaltvorgänge in der Testschaltung kommutiert der Strom aus dem Zweig
mit Mosfet und Zwischenkreiskondensator in den Diodenzweig und umgekehrt. Ein
solcher Schaltvorgang kann betrachtet werden als Überlagerung eines stationären Stroms
mit einem zusätzlichen transienten Strom.

Koninklijke Philips Electronics N.V. 2009
37
PR-TN 2009/00487
Unclassified
Abbildung 21: Überlagerungsprinzip während eines Schaltvorgangs
Im vorliegenden Fall wird nach Abbildung 21 der stationäre Strom I1 angenommen.
Diesem Strom I1 wird nun der transiente Kreisstrom I2 überlagert, sodass sich in Summe
I3 ergibt. Die Geschwindigkeit, mit der dieser Kreisstrom aufgebaut werden kann, wird
bestimmt durch die Induktivität der entsprechenden Schleife. Diese kann laut Erickson
[6] abgeschätzt werden durch
L
0  A
l
mit A  Umschlosse ne Fläche
und l  effektive Länge des magnetisch en Pfades
( 37 )
Eine Reduzierung der Induktivität kann also erreicht werden durch Verkleinerung der
eingeschlossenen Fläche und Vergrößerung des magnetischen Pfades durch Verwendung
breiterer Leiterbahnen. Die Anordnung mit der die Minimierung der Fläche angestrebt
wird, ist in Abbildung 22 dargestellt.
Abbildung 22: Anordnung zur Minimierung der Streuinduktivität
38

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Der Kreisstrom I2 umschließt hier die rot markierte Fläche.
Zur Ermittlung der verbleibenden Streuinduktivität wird

die Diode mit Hilfe eines Kupferstreifens durch einen Kurzschluss ersetzt

die Induktivität ausgebaut

der Mosfet bei VDC  50V für wenige Nanosekunden eingeschaltet
und schließlich

der Stromanstieg dID/dt gemessen.
Daraus ergibt sich für die Streuinduktivität ein Wert von
Lstreu  VDC 
t
2,55ns
 50 V 
 26 nH
I D
4,9A
( 38 )
4.3.2. Strommessung
Die Forderung nach der Minimierung der vom transienten Kreisstrom eingeschlossenen
Fläche spricht für die Verwendung eines Shuntwiderstands zur Messung des Stroms.
Eine Stromzange oder Rogowski-Spule würde ein aus der Schaltung herausragendes
Leiterstück erfordern, welches umschlossen werden kann und damit die Fläche A in (37)
vergrößern.
4.3.3. Anordnung der Messpunkte
ie zu messenden Größen sind Strom ID und Spannung VD der Diode. Beide werden als
Spannung gemessen. Spannungsmessungen sollten möglichst mit Massebezug
durchgeführt werden, um Common-Mode-Störungen durch Potentialschwankungen zu
minimieren. Daher bietet sich die in Abbildung 23 gezeigte Messanordnung an.
Abbildung 23: Mögliche Messanordnung 1

Koninklijke Philips Electronics N.V. 2009
39
PR-TN 2009/00487
Unclassified
Abbildung 24: Mögliche Messanordnung 2
VD ergibt sich hier zu:
VD  V2  V1
( 39 )
Allerdings muss in diesem Fall der Mosfet auf hochliegendem Potential eingesetzt
werden. Die parasitäre Kapazität am Ausgang der Treiberstufe liegt dann parallel zur
Diode und beeinflusst die Messung. Als Alternative wird der Mosfet mit
potentialgetrennter Treiberstufe auf der Low-Side eingesetzt und der Pluspol der
Versorgungsspannung auf Massepotential gelegt, sodass die Spannungsmessung weiter
mit Massebezug möglich ist (Abbildung 24).
Abbildung 25: Messschaltung, Ansicht von oben
40

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 26: Messschaltung, Ansicht von unten
4.4.
Auswahl der Komponenten
Die Schaltung wird mit 200 V Gleichspannung betrieben und soll Messungen mit
Vorwärtsströmen von bis zu 4 A ermöglichen. Alle Komponenten, die Teil der
Kommutierungsschleife sind, werden in SMD-Bauweise ausgeführt.
4.4.1. Induktivität
Die Induktivität wird in einlagigem Design ausgeführt, um
Wicklungskapazität klein zu halten. Kenndaten der Induktivität sind:

Kern ETD59/31/22

Kernmaterial 3C94

Effektive Fläche Ae  368 mm 2

Wicklungszahl N = 16

Luftspalt d = 1,8 mm

Induktivität L = 47  H (gemessen bei 1 MHz)

Resonanzfrequenz fres = 14,5 MHz

Parasitäre Kapazität Cpar = 2,6 pF
die
parasitäre
4.4.2. MOSFET
Der Mosfet wird anhand folgender Anforderungen ausgewählt:

Koninklijke Philips Electronics N.V. 2009
41
PR-TN 2009/00487
Unclassified

Kurze Schaltzeiten, um steile Stromflanken zu erreichen

Kleine Ausgangskapazität, um die Messungen möglichst wenig zu beeinflussen

Gutes Leitverhalten bei allen auftretenden Strömen

Ausreichende Sperrfähigkeit
Bei der Auswahl des Mosfets im Hinblick auf die nötige Sperrspannung muss
unterschieden werden zwischen Messungen des Reverse- und des Forward-Recovery.
Die Vorwärtsspannung des Mosfets ergibt sich anhand eines Maschenumlaufs zu:
VT  VDC  VD  VRShunt.
( 40 )
Reverse-Recovery
Es muss die maximale Gleichspannung VDC = 200 V eingestellt sein, um ein möglichst
schnelles Abschalten zu erreichen. Bei höchstem Diodenvorwärtsstrom von 4 A gilt
stationär betrachtet
VD VRShunt  10  15V
( 41 )
sodass eine Sperrfähigkeit von VDSS = 250 V ausreichend ist.
Forward-Recovery
Beim Einschalten der Diode können Spannungen VD von deutlich über 100 V auftreten
(s. Abbildung 37), sodass bei VDC = 200 V eine Sperrfähigkeit von VDSS = 250 V nicht
mehr ausreichend wäre. Abbildung 27 zeigt eine Messung bei VDC = 200 V und 4 A
Vorwärtsstrom. Hier wird durch den Vergleich mit einer fehlerfreien Messung sichtbar,
dass die Diodenvorwärtsspannung bei VDC = 80 V begrenzt wird. Die Spannung über
dem
Mosfet
beträgt
hier
unter
Vernachlässigung
des
Shunts
VT  VDC  VD  200 V  80V  280V .
42

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 27: Begrenzung der Diodenvorwärtsspannung durch Mosfet (blau: VD,
rot: ID, grün: VD aus fehlerfreier Messung)
Da bei der Messung des Forward-Recovery die Diodensperrspannung nicht relevant ist,
kann hier mit kleineren Spannungen VDC gearbeitet werden, sodass eine Sperrspannung
von 250 V stets ausreicht. Dennoch wird deutlich, dass der Forward-Recovery-Effekt
beim Entwurf von Schaltungen unbedingt berücksichtigt werden muss, z.B. in diesem
Fall bei der Auslegung des Mosfets.
Zunächst wurde ein Mosfet vom Typ FDD6N25 (Fairchild) eingesetzt (Tabelle 1).Es
stellte sich jedoch heraus, dass der Drain-Source-Widerstand bei hohem
Diodenrückstrom so weit ansteigt, dass ein hoher Anteil der Betriebsspannung über dem
einschaltenden Mosfet anliegt, damit nicht mehr als Sperrspannung über der Diode zur
Verfügung steht und der Rückstrom begrenzt wird (s. Abbildung 54). Daher wird ein
Mosfet mit höherer Stromtragfähigkeit vom Typ IRFR12N25D (International Rectifier)
ausgewählt (Tabelle 1). Bei sehr hohen Rückströmen ist auch dieser Mosfet nicht gut
geeignet (Abschnitt 5.2.1), sodass zusätzlich ein IRFS4229PbF (International Rectifier)
(Tabelle 1) eingesetzt werden muss, jedoch nur bei hohem Strömen, da die
Schaltgeschwindigkeit des IRFS4229PbF deutlich kleiner ist als beim IRFR12N25D.
Tabelle 1: Verwendete Mosfets
Mosfet
VDSS in V
IDauer in A
IPuls in A
COSS in
pF
ton in ns
toff in ns
FDD6N25
250
4,4
18
38
25
12
IRFR12N25D
250
14
56
130
25
9,2
IRFS4229PbF
250
45
180
390
31
21

Koninklijke Philips Electronics N.V. 2009
43
PR-TN 2009/00487
Unclassified
Zwischenkreiskondensator
Es werden 21 induktivitätsarme 1,2  F Mehrschicht-Keramik-Kondensatoren (MLCC)
mit guten Hochfrequenzeigenschaften und zwei 220  F Elektrolytkondensatoren
eingesetzt. Bei schnellen Ladevorgängen der Induktivität muss die in den MLCC's
gespeicherte Energie ausreichen, um einen Stromaufbau auf 4 A zu gewährleisten. Eine
worst-case-Abschätzung (VDC = 10 V) der entsprechenden Energien liefert:
1
1
 C  V 2   21  1,2F  10V 2  1,26 mJ
2
2
1
1
WC   L  I 2   47 H  4A 2  0,38mJ
2
2
WC 
( 42 )
Der Kapazitätswert der MLCC's ist also ausreichend hoch.
4.4.3. Shuntwiderstand
Der Shuntwiderstand wird aus zwei parallelgeschalteten niederinduktiven PräzisionsChip-Widerständen mit je 4  gebildet. Der Widerstandswert wird verhältnismäßig
hoch gewählt, damit der induktive Spannungsabfall möglichst vernachlässigbar
gegenüber dem ohmschen Anteil ist. Die Vernachlässigbarkeit wird in Abschnitt 5.5.2
überprüft.
4.4.4. Platine
Wie bereits in Abschnitt 4.3.1 beschrieben, soll die vom transienten Kreisstrom
umschlossene Fläche minimiert werden. Dazu wird ein möglichst dünnes Trägermaterial
verwendet. Aus Zeitgründen wurde eine Platine gefräst (Dicke des Trägermaterials
d = 350  m), auch wenn bei der Anfertigung eines PCBs noch dünnere Schichten
möglich gewesen wären.
4.5.
Messtechnik
4.5.1. Oszilloskop
Es wird ein digitales Oszilloskop vom Typ LeCroy Waverunner 6100 eingesetzt. Dies
verfügt über 4 Kanäle mit je 1 GHz Bandbreite.
4.5.2. Tastköpfe
Zur Messung von V1 (s. Abbildung 24) muss ein Tastkopf verwendet werden, der für die
200 V Betriebsspannung der Schaltung geeignet ist. Hier wird ein passiver Tastkopf vom
Typ LeCroy PP007 benutzt. Zur Minimierung von Induktionsschleifen beim Messabgriff
wird auf der Platine eine spezielle Aufsteckvorrichtung (s. Abbildung 25:
44

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Messabgriff PP007) angebracht, sodass der Tastkopf ohne separates Massekabel
auskommt.
Am Shuntwiderstand werden geringere Spannungen V2 (s. Abbildung 24) erwartet,
sodass hier ein aktiver Tastkopf vom Typ LeCroy AP033 Verwendung findet. Dieser
verfügt über eine Bandbreite von 500 MHz und ist für Spannungsmessungen bis 40 V
(differential-mode) geeignet. Es können also mit dem 2  Shuntwiderstand
Rückstromspitzen von 20 A gemessen werden. Laut Hancock [8] entspricht eine
Bandbreite von fBW = 500 MHz bei einer geforderten Genauigkeit von 3 % einer
Kniefrequenz von
f knee 
f BW
 260 MHz .
1,4
( 43 )
Damit können Signalanstiegszeiten (von 10 % auf 90 %) von
Trise 
0,5
 2ns
f knee
( 44 )
gemessen werden. Da die hier zu erwartenden Signalanstiegszeiten länger als 2 ns sind,
ist die Bandbreite der AP033 ausreichend. Eine Aufsteckvorrichtung wie zur Messung
von
V1
wird
auch
am
Shuntwiderstand
vorgesehen,
damit
eine
Synchronisierungsmessung zwischen PP007 und AP033 durchgeführt werden kann, bei
der beide Tastköpfe die gleiche Spannung messen. In Abbildung 55 messen beide
Tastköpfe eine Rechteckspannung am Shuntwiderstand. Die steigende Flanke wird mit
dem passiven Tastkopf PP007 etwa 1 ns gegenüber der Messung mit dem aktiven
Tastkopf AP033 verzögert angezeigt. Dies wird vernachlässigt.

Koninklijke Philips Electronics N.V. 2009
45
PR-TN 2009/00487
5.
Unclassified
Messungen
Es werden drei Silizium-PSN-Dioden und eine SiC-Schottky-Diode untersucht:

BYD57M (Philips Semiconductor), wird im Folgenden zur Verbesserung der
Lesbarkeit als Diode A bezeichnet.

BYG23M (Vishay Semiconductor), im Folgenden als Diode B bezeichnet.

SUF4007 (Diotec Semiconductor), im Folgenden als Diode C bezeichnet.

IDH02SG120 (SiC, Infineon), im Folgenden als Diode~D bezeichnet.
Die wesentlichen Datenblattangaben sind in Tabelle 2 zusammengefasst.
Tabelle 2: Untersuchte Dioden (Anmerkung zur Reverse-Recovery-Zeit: IF=0,5A
über Irr=1A auf IR=0,25A)
Diodentyp
Diode A
Diode B
Diode C
Diode D
Sperrspannung in V
Nennstrom in A
1000
1000
1000
1200
1
1,5
1
2
Reverse-RecoveryZeit in ns
75
75
75
Kein RR
Abbildung 28: Diodensamples (v.l.n.r.: Diode A, C, B, D)
Für alle Dioden wird sowohl das statische (Abschnitt 5.1) als auch das dynamische
(Abschnitt 5.2 und 5.3) Verhalten bei verschiedenen Temperaturen gemessen. Bei der
Messung des dynamischen Verhaltens werden die Parameter Durchlassstrom sowie
Stromsteilheit variiert.
46

Koninklijke Philips Electronics N.V. 2009
Unclassified
5.1.
PR-TN 2009/00487
Statische Messungen
Bei Strom-Spannungs-Kennlinien aus Datenblättern elektronischer Bauelemente handelt
es sich normalerweise um worst-case-Angaben. D.h. die Bauteile verhalten sich in der
Regel günstiger als angegeben. Sie weisen z.B. bei einem bestimmten Strom eine
kleinere Durchlassspannung auf als im Datenblatt angegeben.
Deshalb werden die Strom-Spannungs-Kennlinien der untersuchten Dioden selbst
gemessen. Bei der Messung solcher Kennlinien ist es nicht sinnvoll, die Dioden mit
einem Gleichstrom oder einer Gleichspannung zu versorgen und Spannung bzw. Strom
zu messen. Insbesondere bei höheren Strömen würden die Dioden sich durch die lange
Leitzeit erheblich erwärmen. Dadurch wäre es nicht ohne weiteres möglich, eine
Kennlinie für eine bestimmte Temperatur anzugeben. Die Erwärmung der Dioden wird
hier möglichst klein gehalten, indem der Aufbau aus Kapitel 4 verwendet wird. Es wird
jedoch in diesem Fall nur ein einzelner Puls am Mosfet angelegt, sodass in der
Induktivität ein Strom aufgebaut wird, der in die Diode kommutiert und dann bis auf den
Wert Null abnimmtiii. Während des Abklingvorgangs (Abbildung ) werden Strom ID und
Spannung VD mit dem Oszilloskop aufgenommen und anschließend im I-V-Diagramm
aufgetragen (Abbildung ). Die Stromleitphase dauert etwa 0,5 ms.
Zur Darstellung der Temperaturabhängigkeit werden Messungen bei verschiedenen
Temperaturen bis 175 °C durchgeführt. Dazu werden die Dioden mittels Wärmeleitpaste
an eine Heizplatte gekoppelt. Die Temperaturmessung erfolgt mit PT100-Widerständen,
die mittels Wärmeleitkleber an den Dioden fixiert worden sind.
Zunächst wurden Messungen bei 25 °C, 50 °C, 75 °C usw. bis 175 °C durchgeführt.
Diese waren aufgrund von Quantisierungsfehlern nicht für eine genaue Charakterisierung
der Dioden brauchbar, lassen aber die Aussage zu, dass die Temperaturkurven im
Bereich 25 bis 175 °C linear interpoliert werden können, sofern Messungen bei zwei
Temperaturen vorhanden sind. Deshalb wird bei einer Wiederholung der Messungen nur
bei 25 °C und 125 °C gemessen. Alle anderen Kurven in Abbildung basieren auf
interpolierten Werten.
iii
Hier wurde eine Spule mit L = 500uH verwendet, um sicher zu stellen, dass die Diode ihre stationären
Leiteigenschaften erreicht.

Koninklijke Philips Electronics N.V. 2009
47
PR-TN 2009/00487
Unclassified
Abbildung 29: Messung der statischen Kennlinien
Abbildung 30: Statische Kennlinien
Es zeigt sich, dass die Dioden A und D bei Strömen über 0,5 A deutlich kleinere
Spannungen aufweisen, als im Datenblatt angegeben. Diese Abweichung fällt bei
Diode A bei höheren Temperaturen geringer aus.
Diode C und besonders Diode B stimmen genauer mit den Datenblattwerten überein.
48

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Si-PSN-Dioden weisen bekanntlich mit steigender Temperatur eine sinkende
Vorwärtsspannung auf. Schottky-Dioden verhalten sich genau umgekehrt.
Der direkte Vergleich aller untersuchten Dioden in Abbildung 31 zeigt, dass die
Dioden B, C und D sehr ähnliche Kennlinien haben. Die relative Abweichung
untereinander beträgt hier maximal 20 %. Diode A hingegen weist etwa doppelt so große
Spannungen auf wie die anderen drei Dioden. Ihr statisches Leitverhalten ist also
wesentlich schlechter.
Abbildung 31: Vergleich der statischen Kennlinien bei 25°C (links) und 100°C
(rechts)
5.2.
Reverse-Recovery
5.2.1. Variation des Durchlassstroms
Alle Dioden werden mit Strömen von 500 mA, 1 A, 2 A und 4 A belastet, bevor der
Strom schnellstmöglich abgeschaltet wird. Dabei werden Stromsteilheiten von ungefähr
2 kA/  s erreicht. Die Messungen des Rückstroms und der Diodenspannung sind in
Abbildung 32 dargestellt. Bei der ersten Messung mit 4 A (an Diode B) tritt eine
Begrenzung des Rückstroms durch den steigenden Drain-Source-Widerstand des Mosfets
auf. Deshalb wird bei den anderen Diodentypen für die Messung ein Mosfet mit größerer
Stromtragfähigkeit eingesetzt, der allerdings ein langsameres Schaltverhalten aufweist
(vgl. Abschnitt 4.4.2).
In Abbildung 33 sind die Messungen bei zwei verschiedenen Durchlassströmen zum
Vergleich zusammengestellt. Hier kann festgehalten werden, dass die Dioden B und C
etwa gleich hohe Rückstromspitzen aufweisen. Die Rückstromspitze von Diode A ist
kleiner. Diode B zeigt einen deutlich abrupteren Stromrückgang als die anderen beiden
Si-PSN-Dioden.
Bei der SiC-Schottky-Diode fließt ein kleiner Rückstrom (Abbildung 33). Es handelt sich
um einen kapazitiven Strom, der durch die gegenüber Si-PSN-Dioden deutlich größere
Sperrschichtkapazität verursacht wird. Dieser Rückstrom ist unabhängig vom
Durchlassstrom (Abbildung 32).

Koninklijke Philips Electronics N.V. 2009
49
PR-TN 2009/00487
Unclassified
In Tabelle 3 und 4 sind die Reverse-Recovery-Ladungen Qrr (Abbildung 10) bzw. die
kapazitive Ladung QC der SiC-Schottky-Diode und die Ausschaltverlustenergien Eaus
zusammengestellt. Hier zeigt sich, dass nicht zwangsläufig der Zusammenhang "`Je
größer Qrr, desto größer Eaus"' gelten muss. Denn die Verlustenergien sind bei Diode B
trotz größerer Ladung Qrr teilweise etwas geringer als bei Diode A. Dieser scheinbare
Widerspruch kann gelöst werden, wenn man beachtet, dass die Spannung von Diode A
während Phase 1 (Abschnitt 2.3.2) durch einen höheren Mittelgebietswiderstand schon
deutlich stärker negativ wird (Abbildung 33). Die wesentlich höhere Ladung Qrr von
Diode C resultiert allerdings erwartungsgemäß in höheren Verlustenergien.
Abbildung 32: Reverse-Recovery-Verhalten bei verschiedenen Durchlassströmen
50

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 33: Reverse-Recovery-Verhalten aller Dioden im Vergleich
Tabelle 3: Reverse-Recovery-Ladung Qrr in nC bzw. Sperrschichtladung QC in nC
bei verschiedenen Durchlassströmen
Durchlassstrom
500 mA
1A
2A
4A
Diode A
51
89
157
300
Diode B
61
107
195
340
Diode C
90
160
263
541
Diode D
6,5
6,7
8,1
10,5
Tabelle 4: Ausschaltverlustenergie Eaus in uJ bei verschiedenen Durchlassströmen
Durchlassstrom
500 mA
1A
2A
4A
Diode A
4,0
6,3
10
13
Diode B
3,5
5,3
7,8
11
Diode C
5,6
10
16
28
Diode D
0,7
0,7
1,1
1,7
5.2.2. Variation der Stromsteilheit
Hier wird die Einschaltgeschwindigkeit des Mosfets durch verschieden große
Gatewiderstände (10  , 39  , 100  , 200  und 470  ) verändert, um die
Stromsteilheit dID/dt zu variieren. Abbildung 34 zeigt die gemessenen Strom- und
Spannungsverläufe. Der Durchlassstrom beträgt jeweils 1 A. In Tabelle 5 und 6 sind
wieder die Reverse-Recovery-Ladungen und die Ausschaltverlustenergien
zusammengestellt. Zusätzlich sind die Ausschaltenergien in Abbildung 35 grafisch
dargestellt. Man erkennt, dass die gemessenen Werte für Qrr kleiner werden, je langsamer
der Ausschaltvorgang abläuft. Diese Beobachtung lässt sich dadurch erklären, dass in Qrr
nur der Anteil der gespeicherten Ladung enthalten ist, der tatsächlich aus dem schwach
dotierten Mittelgebiet herausfließt. Zusätzlich nimmt die gespeicherte Ladung auch durch

Koninklijke Philips Electronics N.V. 2009
51
PR-TN 2009/00487
Unclassified
Rekombination ab. Je länger nun der Ausräumvorgang dauert, desto mehr Zeit haben die
Ladungsträger, zu rekombinieren und desto kleiner wird der Anteil von Qrr an der
gesamten gespeicherten Ladung.
Abbildung 35 zeigt, dass die Ausschaltverluste sinken, je langsamer die Dioden
ausgeschaltet werden. Dafür gibt es zwei Gründe: Erstens ist bei langsamen
Ausschaltvorgängen die Ladung Qrr kleiner, da sich der Ladungsträgerabbau durch
Rekombination stärker auswirkt und zweitens ergeben sich bei geringeren
Stromsteilheiten niedrigere Rückstromspitzen.
Abbildung 34: Reverse-Recovery-Verhalten bei verschiedenen Stromsteilheiten
Tabelle 5: Reverse-Recovery-Ladung Qrr in nC bei verschiedenen Stromsteilheiten
dID/dt
-2 kA/  s
-440 A/  s
-180 A/  s
-100 A/  s
-35 A/  s
Diode A
89
91
83
65
43
Diode B
109
113
96
95
64
Diode C
160
156
150
137
115
Tabelle 6: Ausschaltverlustenergien Eaus in uJ bei verschiedenen Stromsteilheiten
dID/dt
-2 kA/  s
-440 A/  s
-180 A/  s
-100 A/  s
-35 A/  s
52
Diode A
6,5
3,8
2,3
1,4
0,5
Diode B
5,3
3,4
2,0
1,7
0,6

Diode C
11
7,3
6,4
4,9
2,7
Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 35: Ausschaltenergien der Dioden in Abhängigkeit von der Stromsteilheit
5.2.3. Variation der Temperatur
Die bisherigen dynamischen Messungen sind bei Raumtemperatur (25 °C) durchgeführt
worden. Jedoch ist dieser Betriebszustand für anwendungsbezogene Simulationen kaum
relevant, da in den Dioden durch elektrische Verluste Wärme entsteht, die über einen
thermischen Widerstand an die Umgebung abgegeben werden. Dadurch erhöht sich die
Temperatur der Dioden. Um Simulationen auch für höhere Temperaturen durchführen zu
können, werden zusätzliche Messungen bei einer Temperatur von 125 °C durchgeführt.
Diese Temperatur wird bei der Auslegung leistungselektronischer Schaltungen oft als
Maximaltemperatur angenommen, da sich z.B. bei Mosfets oberhalb dieser Temperatur
oft kein stabiler Arbeitspunkt mehr einstellt.
Für alle anderen Temperaturen kann eine lineare Interpolation durchgeführt werden. Auf
Basis der durchgeführten Messungen kann jedoch keine Aussage über die Genauigkeit
von interpolierten Werten getroffen werden. Sicher ist nur, dass die bei 125 °C
ermittelten Schaltverluste für worst-case-Betrachtungen genutzt werden können.
Oberhalb von 125 °C ist keinerlei Aussage bezüglich der Schaltverluste möglich, sodass
eine Extrapolation der Messdaten zu höheren Temperaturen nicht zu brauchbaren
Ergebnissen führen kann.
In Abbildung 36 sind Messkurven für Durchlassströme von 500 mA und 1 A bzw. 2 A
bei verschiedenen Temperaturen dargestellt. Daraus und anhand von Tabelle 7 lässt sich
erkennen, dass die gespeicherte Ladung bei höheren Temperaturen deutlich zunimmt. Bei
den Dioden A und B um den Faktor 2, bei Diode C beträgt der Faktor etwa 1,6. Damit
verbunden nehmen auch die Ausschaltverlustenergien um jeweils ungefähr den gleichen
Faktor zu (Tabelle 8).

Koninklijke Philips Electronics N.V. 2009
53
PR-TN 2009/00487
Unclassified
Abbildung 36: Reverse-Recovery-Verhalten bei verschiedenen Temperaturen
Tabelle 7: Reverse-Recovery-Ladung Qrr in nC bei verschiedenen Durchlassströmen
und Temperaturen
Durchlassstrom
500 mA @ 25 °C
500 mA @ 125 °C
1 A @ 25 °C
1 A @ 125 °C
2 A @ 25 °C
2 A @ 125 °C
Diode A
52
110
89
177
-
Diode B
62
122
106
202
-
Diode C
100
157
263
425
Tabelle 8: Ausschaltverlustenergien Eaus in uJ bei verschiedenen Durchlassströme
und Temperaturen
Durchlassstrom
500 mA @ 25 °C
500 mA @ 125 °C
1 A @ 25 °C
1 A @ 125 °C
2 A @ 25 °C
2 A @ 125 °C
5.3.
Diode A
3,8
7,5
6,3
11,6
-
Diode B
3,5
7,4
5,8
10,7
-
Diode C
7,7
12,5
16,4
30,3
Forward-Recovery
5.3.1. Variation des Durchlassstroms
Alle Dioden werden mit Strömen von 200 mA, 500 mA, 1 A, 2 A und 4 A belastet.
Dabei wird der Strom schnellstmöglich eingeschaltet, sodass der Stromaufbau jeweils
ungefähr 10 ns dauert. Die Messungen von Diodenstrom und -spannung sind in
Abbildung 37 dargestellt.
54

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
In
Abbildung 37
und
Tabelle 9
können
die
auftretenden
Einschaltspannungsüberhöhungen VFRM an den einzelnen Dioden bei zwei verschiedenen
Durchlassströmen verglichen werden:
Tabelle 9: Vergleich der auftretenden Einschaltspannungsüberhöhungen VFRM in V
Durchlassstrom
1A
4A
Diode A
29
110
Diode B
25
93
Diode C
39
130
Diode D
3
8
Die höchsten Überspannungen (Diode C) liegen etwa 20-40 % über den niedrigsten
(Diode B). Bei Diode D treten bis auf die in Abbildung 37 erkennbaren
Einschwingvorgänge keine Überspannungen durch den Forward-Recovery-Effekt auf.
Das starke Einschwingen lässt sich zurückführen auf die relativ große
Sperrschichtkapazität und die parasitäre Kapazität des Gehäuses (TO-220) sowie die
parasitäre Induktivität des Gehäuses.
In Tabelle 10 sind die Einschaltverlustenergien aufgeführt. Diese werden als
Zusatzverluste zu den ohnehin vorhandenen statischen Verlusten berechnet:
Eein   I D  VD  Vstat dt
t1
t ein
mit tein  Strom - und Spannungsn ulldurchga ng
t1  Zeitpunkt nach Abklingen des Forward - Recovery
( 45 )
und Vstat  Stationäre Diodenspan nung VD I D 
Wie anhand der Abbildung 38 zu erwarten ist, treten die größten Verluste bei Diode C
auf, gefolgt von Diode A. Die geringsten Verluste bei den Si-PSN-Dioden treten, wie
schon beim Ausschalten (Abschnitt 5.2), bei Diode B auf. Bei Diode D liegen die
Einschaltverluste um 1-2 Größenordnungen niedriger.

Koninklijke Philips Electronics N.V. 2009
55
PR-TN 2009/00487
Unclassified
Abbildung 37: Forward-Recovery-Verhalten bei verschiedenen Durchlassströmen
Abbildung 38: Forward-Recovery-Verhalten aller Dioden im Vergleich
Tabelle 10: Einschaltverlustenergien Eein in uJ bei verschiedenen Durchlassströmen
Durchlassstrom
200 mA
500 mA
1A
2A
4A
56
Diode A
0,08
0,3
1
4,2
10
Diode B
0,08
0,3
0,9
3,3
9,8
Diode C
0,1
0,5
1,4
4,3
14,2

Diode D
0,03
0,08
0,14
0,34
Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
5.3.2. Variation der Stromsteilheit
Hier wird die Ausschaltgeschwindigkeit des Mosfets durch verschieden große
Gatewiderstände (10  , 200  , 470  , 1 k  und 3 k  ) verändert, um die
Stromsteilheit dID/dt zu variieren.
Die hier aufgenommenen Messungen sind leicht fehlerhaft (vgl. Abschnitt 5.5.1) und
besitzen daher nur begrenzte Aussagekraft.
Abbildung 39 zeigt die gemessenen Strom- und Spannungsverläufe. In Tabelle 11 sind
wieder die Einschaltverlustenergien zusammengestellt. Die Vergleichbarkeit der Dioden
untereinander ist hier eingeschränkt, da bei den Messungen trotz jeweils gleicher
Gatewiderstände nicht immer einheitliche Stromflanken erzeugt werden (Abbildung 39).
Wie beim Ausschalten so gilt auch hier, dass bei einem langsameren Schaltvorgang
weniger Verluste entstehen, da der Widerstand des Mittelgebiets bis zum Erreichen des
stationären Stroms schon weiter abgesunken ist als bei schnellem Einschalten.
Abbildung 39: Forward-Recovery-Verhalten bei verschiedenen Stromsteilheiten
Tabelle 11: Einschaltverlustenergien Eein in uJ bei verschiedenen Stromsteilheiten
dID/dt
300 A/  s
100 A/  s
50 A/  s
30 A/  s
10 A/  s
Diode A
5,4
3,7
1,2
Diode B
4,8
3,9
3,1
2,1
0,7
Diode C
6,9
5,1
4,5
3,3
1,8
5.3.3. Variation der Temperatur
Es wird die Temperaturabhängigkeit des Forward-Recovery-Verhaltens untersucht. In
Abbildung 40 sind die Messkurven bei verschiedenen Temperaturen für Durchlassströme
von 200 mA, 2 A und 4 A dargestellt. Die Stromsteilheit beträgt bei einem
Durchlassstrom von 4 A jeweils 500 kA/us.
Man erkennt, dass die Überspannungen bei allen drei Si-PSN-Dioden bei 125 °C um 2530 % größer sind als bei Raumtemperatur. Die temperaturabhängigen

Koninklijke Philips Electronics N.V. 2009
57
PR-TN 2009/00487
Unclassified
Einschaltverlustenergien sind nach Tabelle 12 bei 125 °C 30-80 % höher als bei
Raumtemperatur.
Abbildung 40: Forward-Recovery-Verhalten bei verschiedenen Temperaturen
Tabelle 12: Einschaltverlustenergien Eein in uJ bei verschiedenen Durchlassströmen
und Temperaturen
Durchlassstrom
200 mA @ 25 °C
200 mA @ 125 °C
1 A @ 25 °C
1 A @ 125 °C
4 A @ 25 °C
4 A @ 125 °C
5.4.
Diode A
0,08
0,14
1,1
1,7
11,0
15,7
Diode B
0,08
0,12
0,9
1,4
9,5
12,7
Diode C
0,11
0,17
1,2
2,2
14,2
21,7
Gesamtverluste
Die Gesamtverluste der einzelnen Dioden lassen sich frequenzabhängig berechnen:
Pgesamt a, f   Pstat a   Pein  f   Paus  f 
Pstat a   VD I D   I D  a
mit a  Tastgrad
Pein  f   Eein  f
( 46 )
Paus  f   Eaus  f
Für einen bestimmten Betriebszustand können die benötigten Werte aus den Tabellen
und Kennlinien in diesem Kapitel abgelesen und grafisch dargestellt werden.
Beispiel: Mit den Einstellungen
58

Temperatur T = 25 °C

Vorwärtsstrom I = 1 A

Tastgrad a = 0,5

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487

Stromsteilheit beim Abschalten dI D dt   2kA s

Stromsteilheit beim Einschalten dI D dt  300A s
erhält man die in Abbildung 41 gezeigten Verläufe für die Gesamtverluste der Dioden.
Hier wird deutlich, dass die Schaltverluste von Diode D so gering sind, dass selbst bei
Frequenzen von mehreren 100 kHz die Gesamtverluste kaum merklich ansteigen.
Außerdem ist bemerkenswert, dass Diode C bei Frequenzen unter 10 kHz aufgrund der
guten statischen Eigenschaften die geringsten Gesamtverluste aufweist. Das relativ
schlechte dynamische Verhalten führt jedoch dazu, dass ihre Gesamtverluste bei über
230 kHz die höchsten sind.
Abbildung 41: Frequenzabhängige Gesamtverluste der Dioden
5.5.
Sicherung der Messgenauigkeit
5.5.1. Oszilloskop
Bei der Überprüfung der Messgenauigkeit wird festgestellt, dass große Sprünge des
Eingangssignals am 1 M  -Eingang deutlich verzerrt werden. In Abbildung 42 erkennt
man, dass sich diese Verzerrungen im  s-Bereich auswirken.

Koninklijke Philips Electronics N.V. 2009
59
PR-TN 2009/00487
Unclassified
Abbildung 42: Gemessenes Rechtecksignal
Deshalb wird vermutet, dass erste Messungen des Forward-Recovery-Verhaltens bei
denen mit VDC = 200 V gearbeitet wurde, durch diesen Effekt fehlerhaft sind, da der
passive Tastkopf am 1 M  -Eingang angeschlossen istiv. Die Verzerrungen werden wie
folgt rechnerisch kompensiert.
Es wird mit einer Mosfet-Halbbrücke eine periodische Rechteckspannung
(Abbildung 42) erzeugt und mit dem passiven Tastkopf gemessen. Mit der
mathematischen CAD-Software Mathcad wird ein zu dieser Messung passendes
Referenzsignal erzeugt, welches verzerrungsfrei ist. Von diesem Referenzsignal wird
angenommen, dass es das unverzerrte Rechtecksignal darstellt. Das gemessene Signal
und das Referenzsignal werden mittels Fast-Fourier-Transformation in den
Frequenzbereich transformiert und dort dividiert. Das Ergebnis ist eine
Kompensationsfunktion. Eine Forward-Recovery-Messung kann nun ebenfalls in den
Frequenzbereich transformiert werden, um dort mit der Kompensationsfunktion
multipliziert und zurücktransformiert zu werden. Das Ergebnis ist das unverzerrte
Originalmesssignal. Wichtig ist hierbei, dass die Vorgeschichte des Messsignals soweit
bekannt ist, dass etwaige vorige Einschwingvorgänge - soweit sie noch nicht
abgeschlossen sind - mit kompensiert werden können.
Da die auftretende Verzerrung je nach gewählter y-Auflösung, also je nach
Spannungsteiler am Eingang, unterschiedlich ausfällt, muss für jede Einstellung eine
separate Kompensationsfunktion errechnet werden.
Bei Messungen mit VDC = 200 V ergibt sich eine deutliche Abweichung zwischen
Messsignal und kompensiertem Signal. Diese Messungen müssen kompensiert werden.
Dagegen ist bei VDC = 10 V der Amplitudenfehler durch die Verzerrung gegenüber der
Einschaltspannungsüberhöhung vernachlässigbar. Hier ist also keine Kompensation
nötig.
Die vorliegenden Messungen in Abschnitt 5.3.2 sind Forward-Recovery-Messungen mit
VDC = 200 V und daher fehlerhaft. Bei der Durchführung der Messungen war allerdings
noch nicht bekannt, dass entweder eine Kompensation notwendig wäre oder mit kleiner
iv
60
Der aktive Tastkopf nutzt den 50

Eingang. Die Strommessung ist deshalb nicht betroffen.

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Spannung VDC gemessen werden müsste. Deshalb wurde die Vorgeschichte der Messung
nicht weit genug aufgezeichnet, um eine Kompensation zu ermöglichen. Eine erneute
Messung war aus Zeitgründen nicht mehr möglich. Alle anderen Messungen müssen
nicht kompensiert werden.
5.5.2. Einfluss der Schaltungsumgebung
Es wird untersucht, ob in ID signifikante parasitäre kapazitive
Signalanteile enthalten sind.
oder induktive
Parasitäre Kapazitäten
Zur Überprüfung wird die Diode aus der Testschaltung entfernt und ein einzelner Puls
am Mosfet angelegt. Beim Vorhandensein einer nennenswerten Kapazität an der Stelle
des durch Entfernen der Diode entstandenen Leerlaufs wäre ein Strom messbar, der diese
auflädt.
Abbildung 56 zeigt jedoch, dass kein bemerkenswerter Strom gemessen wird, sodass die
parasitäre Kapazität an dieser Stelle vernachlässigt werden kann.
Parasitäre Induktivitäten
Die Messung des Diodenstroms erfolgt als Spannungsmessung über einem
Shuntwiderstand. Dabei muss die parasitäre Induktivität des Widerstands berücksichtigt
werden, da sehr steile Stromflanken (bis 2 kA/  s) auftreten. Daher wird erstens der
Widerstandswert mit 2  von vornherein groß gewählt und zweitens eine
Kontrollmessung durchgeführt.
Bei der Kontrollmessung wird mit einem Pulsgenerator eine periodische
Reckteckspannung an den Shuntwiderstand angelegt, dem ein hochohmiger Widerstand
vorgeschaltet ist. Dieser Vorwiderstand bewirkt, dass das Rechtecksignal dem kleinen
Shuntwiderstand als Stromsignal erscheint. Die Spannung über dem Shuntwiderstand
wird gemessen. Ein induktiver Anteil an der Impedanz des Shuntwiderstands würde
durch ein Überschwingen der Spannung erkennbar werden. In Abbildung 57 ist jedoch
kein Überschwingen erkennbar, sodass die Induktivität des Shuntwiderstands
vernachlässigt werden kann

Koninklijke Philips Electronics N.V. 2009
61
PR-TN 2009/00487
6.
Unclassified
Simulationen
In diesem Kapitel wird ein Simulationsmodell entwickelt, das anhand der Messungen in
Kapitel 5 das Verhalten der Dioden nachbildet und zur Simulation in PSpice geeignet ist.
Es erfolgt ein Vergleich von Simulations- mit Messergebnissen anhand dessen eine
Betrachtung der Gültigkeit und Grenzen des Modells vorgenommen wird.
6.1.
Modellansatz
Das Modell ist angelehnt an das Diodenmodell von Lauritzen und Ma [13], welches mit
der Methode der konzentrierten Ladungen (vgl. Abschnitt 3.2.1) realisiert wird. Bei der
Modellierung wird von einer Einsicht in den halbleitertechnischen Aufbau von Si-PSNDioden und die bekannten physikalischen Vorgänge (s. Abschnitt 2) ausgegangen.
Hieraus wird die Grundstruktur des Modells abgeleitet.
Bei der detaillierteren Implementierung werden zur Vereinfachung keine realen,
physikalischen Parameter (z.B. Dotierungsprofil, Geometriedaten, usw.) mehr verwendet.
Vielmehr wird Wert darauf gelegt, eine möglichst gute Übereinstimmung mit den
Messergebnissen zu erzielen.
6.1.1. Modellierungstechnik
Das Modell wird in Orcad Capture zur Simulation mit PSpice implementiert. Die
Beziehungen zwischen den Modellvariablen werden mit Hilfe von Analog Behavioral
Models (ABMs) dargestellt [4]. Mit ABMs können mathematische Gleichungen,
Tabellen und Übertragungsfunktionen in Capture sehr einfach eingegeben werden. Diese
werden zur Simulation mit PSpice automatisch in entsprechende Teilschaltungen
umgewandelt. Durch die Verwendung von ABMs ergibt sich eine übersichtliche
Modelldarstellung als Blockschaltbild (s. S. 79).
6.1.2. Grundstruktur
Si-PSN-Dioden lassen sich durch ein Ersatzschaltbild aus Sperrschichtkapazität Cj und
Bahnwiderstand RM darstellen. Der Zusammenhang zwischen der Ladung in der
Raumladungszone und der Diffusionsspannung ähnelt der Kapazitätsformel [16], sodass
hierfür der Begriff der Sperrschichtkapazität (auch als Raumladungskapazität bezeichnet)
benutzt wird. Der Bahnwiderstand wird durch den elektrischen Widerstand des
Halbleitermaterials und den Anschluss am Halbleiter verursacht.
Es stellt sich die Frage, ob es sinnvoller ist, diese beiden Elemente in Reihe oder parallel
anzuordnen. Dazu wurden Messungen am Impedanzspektrometer mit negativer
Vorspannung durchgeführt. Diese ergaben, dass sich die Impedanz der PSN-Dioden am
ehesten durch die Reihenschaltung von Widerstand und Kapazität darstellen lässt. Dieses
Ersatzschaltbild wird in abgewandelter Form im Modell verwendet (Abbildung 43). Die
Spannung an den äußeren Klemmen entspricht der Summe aus Sperrschichtspannung
und Spannung über dem ohmschen Widerstand.
62

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 43: Modellgrundstruktur
VD  Ve  VRM
( 47 )
Der Strom ID durch die Diode ist jedoch nicht, wie bei einer tatsächlichen
Reihenschaltung von Kapazität und Widerstand, in beiden Elementen gleich groß,
sondern teilt sich an der Kapazität nach (48) in einen Strom Ie, der über die
Sperrschichtkapazität Cj mit der Sperrschichtspannung Ve verknüft ist, und den Strom Ij
auf.
I D  I RM  I j  I e
( 48 )
Ij wird weiter aufgeteilt in den Vorwärtsstrom IF, den Durchbruchstrom IBD, der bei
hohen Sperrspannungen auftritt, sowie den Strom IR der den Diodenrückstrom
wiedergibt:
I j  I F  I BD  I R
6.2.
( 49 )
Stationäres Verhalten
In Abschnitt 3.3 wurde bereits erwähnt, dass die Modellierung des stationären Verhaltens
in den dort vorgestellten Modellen recht aufwendig realisiert wird. Im Gegensatz dazu
wird das stationäre Verhalten in dem hier aufgebauten Modell sehr genau und trotzdem
einfach implementiert. Dazu ist lediglich die Kenntnis der Strom-Spannungs-Kennlinie
erforderlich. Diese kann als Tabelle in einen ABM-Block eingegeben werden und
verknüpft den Vorwärtsstrom IF in der Diode mit der Spannung an den Klemmen VD.

Koninklijke Philips Electronics N.V. 2009
63
PR-TN 2009/00487
Unclassified
Abbildung 44: Implementierung des statischen Verhaltens
In Abbildung 44 ist zu sehen, dass der stationäre Vorwärtsstrom IF mittels einer
algebraischen Schleife aus der Sperrschichtspannung Ve berechnet wird. Die
stromabhängige Spannung über dem Bahnwiderstand wird zur Sperrschichtspannung
addiert. Man erhält die Klemmenspannung, aus der wiederum der Vorwärtsstrom
tabellarisch ermittelt wird. Sobald die Funktion RM(IF) durch die Parametrierung des
Modells bekannt ist, kann die Funktion IF(Ve) explizit, z.B. mit Hilfe einer Tabelle,
angegeben werden. Unter Umständen tritt jedoch der Fall auf, dass sich durch ungünstige
Wahl der Funktion RM(IF) für
positive Ströme IF teilweise negative Spannungen Ve ergeben. Dadurch ist keine
eindeutige Zuordnung IF(Ve) möglich und die Funktion IF(Ve) kann nicht explizit
angegeben werden. Negative Sperrschichtspannungen bei positivem Vorwärtsstrom sind
zwar physikalisch nicht möglich, sodass hier ein Widerspruch vorliegt. Solange das
äußere Verhalten der Diode jedoch richtig wiedergegeben wird, wird dieser Widerspruch
hingenommen, da die physikalische Genauigkeit und die inneren Zustände der Diode
nicht im Vordergrund der Modellierung stehen.
6.3.
Transientes Verhalten
Im Gegensatz zum Modell von Lauritzen und Ma verwendet das hier vorgestellte Modell
nur einen Ladungsknoten nsn*, um die Ladung im Mittelgebiet darzustellen. Gemäß den
Ausführungen in Abschnitt 2.3 baut sich die
Ladungsträgerkonzentration bei
sprungartigem Ein- oder Ausschalten des Stroms exponentiell auf bzw. ab. Daher wird
nsn* mit Hilfe einer Tiefpassfilterung des Stroms Ij berechnet (Abbildung 45). Die
Zeitkonstante entspricht nach der Theorie der Ladungsträgerlebensdauer bei starker
Injektion  HL .
Abbildung 45: Berechnung der mittleren Ladungsträgerkonzentration im
Mittelgebiet
64

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
nsn* nimmt also nach einer ausreichend langen Zeit den gleichen Wert an wie Ij. Somit
stellt nsn* lediglich ein Maß für die Ladungsträgerkonzentration dar. Die Angabe eines
Zahlenwertes, welcher der tatsächlichen Ladungsträgerkonzentration entspricht, ist nicht
möglich, aber für die Wiedergabe des äußeren Verhaltens auch nicht nötig.
6.3.1. Reverse-Recovery
Beim Ausschalten der Diode ist der Strom in Phase 1 (Abbildung 10) zunächst durch die
äußere Beschaltung eingeprägt (Abschnitt 3.2.1). Solange der Strom positiv ist,
entspricht der Diodenstrom dem Stromanteil IF. Da IF nicht negativ werden kann,
übernimmt IR den Diodenstrom, sobald dieser negativ wird.
Für IR gilt folgende Rechenvorschrift:


V 
I R  MaxMin rr ;0; Min  rr  nsn *;0
 Rrr 


( 50 )
Der Term Vj/Rrr entspricht dem eingeprägten Strom, sobald dieser negativ geworden ist.
Der Term  rr  nsn * folgt der abnehmenden Ladungsträgerkonzentration im
Mittelgebiet, skaliert mit dem Faktor   rr .
Die Minimalwertbildung beschränkt IR auf negative Werte.
Im Modell von Lauritzen und Ma [13] wird die Rückstromspitze dann erreicht, wenn die
Ladungsträgerkonzentration am Rand des Mittelgebietes einen Wert sehr nahe bei Null
erreicht. Im hier vorliegenden Modell ist das Erreichen der Rückstromspitze dadurch
gekennzeichnet, dass der eingeprägte Strom Vj/Rrr den gleichen Wert annimmt wie die
mit   rr skalierte Mittelgebietskonzentration. Dieser Zusammenhang ist in
Abbildung 46 ersichtlich.
Abbildung 46: Realisierung des Reverse-Recovery-Verhaltens

Koninklijke Philips Electronics N.V. 2009
65
PR-TN 2009/00487
Unclassified
Nach dem Abreißen des Rückstroms gilt dann:
I j  I R  rr  nsn *
( 51 )
I j  nsn *
dt
( 52 )
Aus Abbildung 45 folgt:
nsn *  
 HL
Einsetzen von (51) in (52) liefert:
nsn *  
  rr  nsn * nsn *
dt
 HL
 rr  1
 nsn *dt
 HL
dn *
 1
 sn   rr
 nsn *
dt
 HL
 nsn *   
( 53 )
nsn* nimmt ebenso wie qm in (27) exponentiell ab und damit gilt für den Rückstrom:
I R t   I R0  e
mit  eff 

t
 eff
( 54 )
 HL
 rr  1
6.3.2. Forward-Recovery
Zur Wiedergabe des Forward-Recovery-Effektes wird der Bahnwiderstand RM des
Mittelgebietes nicht wie im stationären Fall aus dem Vorwärtsstrom berechnet
(Abbildung 44), sondern aus nsn*. Damit wird berücksichtigt, dass RM mit steigender
Mittelgebietskonzentration allmählich fällt.
RM wird analog zu (30) berechnet:
RM 
RM0
nsn *  rsn  1
( 55 )
Damit wird die in (16) eingeführte Leitwertmodulation berücksichtigt. Im stationären
Zustand gilt nämlich:
66

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
nsn *  I F
und VRM  RM  I F
 VRM 
RM0
 IF
nsn *  rsn  1
 VRM 
RM0
I
 rsn  I F  1 F
( 56 )
Für Ströme ab einer Größe von wenigen 100 mA gilt aufgrund typischer Werte für rsn .
rsn  I F  1
( 57 )
und damit:
VRM 
VRM 
RM0
I
 rsn  I F F
RM0
 rsn
( 58 )
 const
Durch die Verwendung von nsn* als mittlere Ladungsträgerkonzentration wird implizit
eine zu jedem Zeitpunkt homogene Ladungsträgerverteilung im Mittelgebiet
angenommen. Bei einem Einschaltvorgang werden die Ladungsträger jedoch aus den
hochdotierten Randgebieten ins Mittelgebiet injiziert. Ein sprungförmiger Stromanstieg
mit sehr steiler Flanke führt dann dazu, dass die mittlere Ladungsträgerkonzentration
schon einen relativ hohen Wert erreicht haben kann, obwohl im Zentrum des
Mittelgebietes noch gar keine Konzentrationsanhebung stattgefunden hat. Dort ist der
Widerstand also noch sehr hoch. Der Gesamtwiderstand des Mittelgebietes ist dadurch
unter Umständen wesentlich höher, als es die mittlere Ladungsträgerkonzentration
vermuten ließe.
Der Rückgang des Bahnwiderstands ist also gegenüber dem Anstieg der
Ladungsträgerkonzentration nochmals verzögert. Dieser Effekt wird im Modell durch
den Einsatz eines zusätzlichen Verzögerungsgliedes mit der Zeitkonstanten  fr modelliert
(Abbildung 47).
Abbildung 47: Berechnung des Forward-Recovery-Widerstandes

Koninklijke Philips Electronics N.V. 2009
67
PR-TN 2009/00487
6.4.
Unclassified
Parameterextraktion
Im hier entwickelten Modell werden sechs Parameter verwendet (  rr ,  HL , Rrr, RM0, rsn
und  fr ). Außerdem muss die statische Kennlinie sowie die Abhängigkeit der
Sperrschichtkapazität von der Sperrschichtspannung aus Messungen oder
Datenblattangaben bekannt sein.
Im Folgenden wird beschrieben, wie die einzelnen Parameter bestimmt werden.
6.4.1. Reverse-Recovery
Gemäß (54) nimmt der Strom nach Erreichen der Rückstromspitze exponentiell mit der
Zeitkonstante  eff   HL rr  1 ab.  eff kann also aus den Messkurven abgelesen werden.
 HL und  rr können dann unter Beibehaltung von  eff so lange variiert werden, bis die
bestmögliche Kurvenanpassung zwischen Simulation und Messung erreicht ist.
Während Phase 1 des Reverse-Recovery (Abbildung 10) sinkt die äußere
Diodenspannung bereits sichtbar ab (siehe z.B. Abbildung 33). Hierfür ist zum Einen der
Bahnwiderstand des Mittelgebietes verantwortlich. Zum Anderen sinkt auch die
Sperrschichtspannung gemäß (19) durch die Abnahme der Ladungsträgerkonzentration
am Übergang zwischen RLZ und Mittelgebiet bereits leicht ab.Dieser Effekt wird hier
mit Hilfe von
Ve  Rrr  I R
( 59 )
approximiert.
6.4.2. Forward-Recovery
Die Parameter RM0, rsn und  fr werden verwendet, um das Forward-RecoveryVerhalten anzupassen. RM0 kann abgeschätzt werden, indem man
Rt  
VD t 
I D t 
( 60 )
aus den Messungen berechnet und R(t) kurz nach dem Einschalten des Stroms betrachtet.
rsn und  fr können dann durch Anpassen von Simulationen und Messungen gefunden
werden.
Die Parameter für die in Kapitel 5 vermessenen Si-PSN-Dioden sind in Tabelle 13
zusammengestellt.
68

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Tabelle 13: Parametrisierung des Modells für die vermessenen Dioden
 rr
 HL
Rrr
RM0
rsn
 fr
BYD@25°C BYD@125°C BYG@25°C BYG@125°C SUF@25°C SUF@125°C
20
27
42
56
30
40
84
112
86
171
124
164
0,1
0,1
0,1
0,1
0,1
0,1
25
35
23
32
27
40
50
50
50
50
50
50
250
250
150
150
150
150
Im folgenden Abschnitt werden Messungen und Simulationen für Diode A exemplarisch
miteinander verglichen. Die entsprechenden Darstellungen für die anderen Dioden sind
im Anhang (A.2.2) zu finden.
6.5.
Vergleich von Simulationen und Messungen
6.5.1. Reverse-Recovery
Die reale Messschaltung wird in PSpice nachgebildet und zur Simulation der
Ausschaltvorgänge verwendet.
Das Reverse-Recovery-Verhalten wird mit guter Genauigkeit wiedergegeben
(Abbildung 48). Lediglich bei hohen Temperaturen wird Irr bei 500 mA nach Anpassung
von Irr bei 1 A zu niedrig berechnet. Irr liegt hier fast 20 % unter dem entsprechenden
Messwert. Es kann ggf. der Parametersatz noch verbessert werden, um die Genauigkeit
zu erhöhen.
Bei der Simulation der Diodenspannung in Phase 2 des Reverse-Recovery
(Abbildung 10) ergeben sich grobe Abweichungen gegenüber den Messungen. Die
Diodenspannung wird jedoch in diesem Bereich nicht von der Diode selbst bestimmt,
sondern durch die äußere Beschaltung. Die Abweichungen kommen also zum Großteil
durch eine ungenaue Nachbildung der Messschaltung zustande. Das Diodenmodell ist
hierfür nicht verantwortlich.

Koninklijke Philips Electronics N.V. 2009
69
PR-TN 2009/00487
Unclassified
Abbildung 48: Reverse-Recovery bei 25 °C
Abbildung 49: Reverse-Recovery bei 125 °C
70

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
6.5.2. Forward-Recovery
Zur Simulation der Einschaltvorgänge
Dioden eingeprägt. Dazu werden aus
erzeugt, mit denen eine Stromquelle
Stromkurven in Abbildung 50 und 51
gemessenen Stromkurven überein.
werden die gemessenen Stromverläufe in die
den Strommessdaten PSpice-Stimulus-Dateien
gesteuert wird. Daher sind die simulierten
nicht zu sehen. Sie stimmen exakt mit den
Insgesamt wird eine gute Genauigkeit erreicht. Die Spannungsspitzen VFRM werden bei
25 °C mit einer Genauigkeit von 2 % berechnet. Es fällt jedoch auf, dass die simulierten
Spannungsverläufe ihren Maximalwert stets wenige Nanosekunden später erreichen als
gemessen. Diese Verzögerung tritt auch bei den Simulationen von Lauritzen und Ma [14]
und ebenso bei Mantooth [15] auf. Es wird keine Erklärung dafür angegeben. Bei 125 °C
tritt die größte Abweichung bei 4 A Vorwärtsstrom auf. Die simulierte Spannungsspitze
ist 10 % höher als gemessen.
Abbildung 50: Forward-Recovery bei 25 °C

Koninklijke Philips Electronics N.V. 2009
71
PR-TN 2009/00487
Unclassified
Abbildung 51: Forward-Recovery bei 125 °C
6.6.
Gültigkeit und Grenzen des Modells
In Abschnitt 6.5 wird das simulierte Verhalten der Dioden mit dem gemessenen
verglichen. Es ergibt sich eine gute Übereinstimmung in einem weiten Arbeitsbereich.
Lediglich bei hohen Strömen bzw. hohen Temperaturen lassen sich deutlichere
Abweichungen feststellen. Hier macht sich bemerkbar, dass bei der Modellierung
teilweise von starken Vereinfachungen ausgegangen wurde.
Bei der Simulation einzelner Schaltvorgänge wird damit eine befriedigende Genauigkeit
erreicht. Für Temperaturen zwischen 25 und 125 °C kann eine Interpolation durchgeführt
werden. Nach Abschnitt 5.1 wird das statische Verhalten durch eine lineare Interpolation
mit guter Genauigkeit wiedergegeben. Eine Aussage zur Genauigkeit des dynamischen
Verhaltens bei Interpolation kann ohne weitere Messungen bei Zwischentemperaturen
nicht getroffen werden. Da bei höheren Temperaturen größere Schaltverluste auftreten
als bei niedrigen Temperaturen, lassen sich die Daten bei 125 °C für worst-caseAbschätzungen bzgl. der Schaltverluste nutzen. Eine Extrapolation zu Temperaturwerten
außerhalb des Messintervalls ist nicht ratsam, da hier keine Aussage über die
Entwicklung der Schaltverluste getroffen werden kann.
Eine deutliche Einschränkung der Gültigkeit ergibt sich aus dem Modellansatz mit nur
einem Ladungsknoten, der die mittlere Ladungsträgerkonzentration im Mittelgebiet
repräsentiert. Dadurch wird implizit von einer homogenen Verteilung der Ladungsträger
ausgegangen. Bei einem schnellen Einschaltvorgang stellt sich aber zunächst eine stark
72

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
inhomogene Ladungsträgerverteilung ein, wodurch der Rückgang des Bahnwiderstands
gegenüber dem Anstieg der Ladungsträgerkonzentration noch mal verzögert wird. Dieser
Effekt wird hier durch den Einsatz eines zusätzlichen Verzögerungsgliedes modelliert
(Abschnitt 6.3.2).
Vergleicht man allerdings die räumliche Verteilung der Ladungsträger während des Einund Ausschaltens (Abbildung 12 und 11), so stellt man fest, dass der
Konzentrationsaufbau sich deutlich vom Konzentrationsabbau unterscheidet. Beim
Ausschalten werden die Ladungsträger von den Rändern her aus dem Mittelgebiet
entfernt. Fällt die Konzentration an den Rändern bis auf die Dotierungskonzentration ab,
so beginnt die Diode zu sperren. Der Bahnwiderstand ist dann bereits wieder sehr hoch.
Bedingt durch das eingeführte zusätzliche Verzögerungsglied steigt der Bahnwiderstand
des Modells allerdings beim Ausschalten deutlich langsamer an als in der Realität.
Daraus folgt, dass das Forward-Recovery nach einem Ausschaltvorgang erst nach
ungefähr 2  s wieder korrekt simuliert wird. Vorher hat der Bahnwiderstand noch nicht
wieder den richtigen Wert erreicht.
Bei der Simulation mehrerer Schaltzyklen ist das Modell ist dieser Form also nur
einsetzbar, wenn zwischen Aus- und Wiedereinschalten der Dioden mindestens 2  s
liegen. Bei einem Tastgrad von 50 % entspräche dies einer Schaltfrequenz von immerhin
250 kHz. Beträgt der Tastgrad allerdings z.B. 10 %, so ergibt sich eine Frequenz von nur
noch 50 kHz.

Koninklijke Philips Electronics N.V. 2009
73
PR-TN 2009/00487
7.
Unclassified
Zusammenfassung und Ausblick
In dieser Arbeit wird ein Modell von Hochspannungs-Si-PSN-Dioden zur Verwendung
in Schaltungssimulatoren (PSpice) entwickelt, das sich an ein aus der Literatur bekanntes
Modell anlehnt. Die Modellgleichungen und damit die Grundstruktur des Modells
basieren auf der Halbleiterphysik. Bei der detaillierteren Implementierung wird jedoch in
erster Linie die Übereinstimmung mit dem gemessenen Verhalten angestrebt, auch wenn
sich dadurch etwaige physikalische Ungenauigkeiten oder Widersprüche ergeben. Neben
dem stationären Verhalten werden insbesondere die transienten Vorgänge modelliert.
Dabei werden gleichermaßen die Einschalt- und die Ausschaltverzögerung (Forwardund Reverse-Recovery) behandelt.
Es werden verschiedene Modellierungsansätze aus der Literatur vorgestellt, bewertet und
in Bezug zum hier entwickelten Modell gesetzt, welches als einfache Form der Methode
der konzentrierten Ladungen realisiert wird.
Zur Verifizierung des Modells werden experimentelle Messungen an drei verschiedenen
Si-PSN-Dioden durchgeführt. Dabei werden die Randbedingungen (Durchlassstrom,
Stromsteilheit, Temperatur) über den gesamten praktisch relevanten Arbeitsbereich
variiert. Die Messungen werden mit einer Testschaltung durchgeführt, deren Auswahl,
Entwurf und Inbetriebnahme Teil dieser Arbeit sind. Es werden wichtige Strategien und
Kriterien für den Schaltungsentwurf behandelt.
Der Vergleich von simuliertem und gemessenem Verhalten zeigt, dass sich in einem
weiten Bereich eine gute Übereinstimmung erreichen lässt. Deutlichere Abweichungen
werden lediglich bei hohen Strömen und hohen Temperaturen sichtbar.
Auch das Forward-Recovery, welches gegenüber dem Reverse-Recovery bisher deutlich
weniger Beachtung unter Schaltungentwicklern findet, wird mit guter Genauigkeit
dargestellt.
Der Spannungsverlauf im Forward-Recovery wird im hier entwickelten Modell durch
den Einsatz eines zweiten Verzögerungsgliedes bei der Berechnung des transienten
Bahnwiderstands simuliert. Beim Ausschalten ergibt sich hierdurch ein zu stark
verzögerter Wiederanstieg des Bahnwiderstands. Daraus resultiert, dass ein
anschließendes Wiedereinschalten erst nach ungefähr 2  s korrekt dargestellt wird,
obwohl bei den hier simulierten Dioden der Reverse-Recovery-Vorgang schon nach
maximal 100 ns abgeschlossen ist.
Soll das Modell für die Simulation mehrerer Schaltzyklen, in denen zwischen Aus- und
Einschalten weniger als 2  s liegen, verwendet werden, so muss an dieser Stelle eine
andere Lösung gefunden werden.
Das Modell soll für die Simulation von Hochspannungsdioden in einem
Röntgengenerator verwendet werden. Hierfür wird auch die alternative Verwendung von
SiC-Schottky-Dioden betrachtet. Diese werden mit der aufgebauten Testschaltung
vermessen. Es wird eine beträchtliche Reduzierung der Schaltverluste festgestellt. Die
stationären Verluste liegen im gleichen Bereich wie die der Si-PSN-Dioden. Eine
74

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
frequenzabhängige Betrachtung der Gesamtverluste der Dioden zeigt, dass durch den
Einsatz von SiC-Schottky-Dioden eine erhebliche Leistungssteigerung bei hohen
Schaltfrequenzen möglich ist.
Eine mögliche Weiterentwicklung des in dieser Arbeit vorgestellten Modells könnte
darin bestehen, den Wiederanstieg des Bahnwiderstands nach dem Ausschalten korrekt
darzustellen und damit den Gültigkeitsbereich des Modells auf höhere Schaltfrequenzen
auszuweiten.
Desweiteren ist bisher keine konkrete Bewertung des Modells im Hinblick auf
Rechenaufwand und -genauigkeit im Vergleich zu anderen, bekannten Modellen erfolgt.
Dies könnte Gegenstand weiterer Untersuchungen sein. Dazu müssten die
entsprechenden Modelle implementiert und eine Anpassung auf die hier vermessenen
Dioden vorgenommen werden.

Koninklijke Philips Electronics N.V. 2009
75
PR-TN 2009/00487
Unclassified
A Anhang
A.1
Messschaltung
A.1.1
Layout
Abbildung 52: Messschaltung Top Layer
Abbildung 53: Messschaltung Bottom Layer
76

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
A.1.2
Auswahl des MOSFETs
Abbildung 54 zeigt, wie der Rückstrom (rot) durch den Drain-Source-Widerstand des
Mosfets begrenzt wird. Die Diodenspannung ist in blau dargestellt.
Abbildung 54: Begrenzung des Rückstroms
A.1.3
Synchronisierung der Tastköpfe
Abbildung 55: Bestimmung des Laufzeitunterschiedes zwischen AP033 und PP007
Blau: VRShunt gemessen mit AP033
Rot: VRShunt gemessen mit PP007

Koninklijke Philips Electronics N.V. 2009
77
PR-TN 2009/00487
A.1.4
Unclassified
Untersuchung auf parasitäre Kapazitäten und Induktivitäten
Abbildung 56: Untersuchung der Testschaltung auf parasitäre Kapazitäten
Abbildung 57: Untersuchung des Shuntwiderstands auf induktive Anteile
Blau: VRShunt gemessen mit AP033
Rot: VRShunt gemessen mit PP007
78

Koninklijke Philips Electronics N.V. 2009
Unclassified
A.2
PR-TN 2009/00487
Simulationen
A.2.1
Modellierungstechnik
Auf Seite 79 unten ist zu sehen, wie das in dieser Arbeit entwickelte Diodenmodell
konkret implementiert wird. Bei der Beschreibung des Modells in Kapitel 6 wurden die
Parameter- und Variablenbezeichnungen so verändert, dass sie mit den in Kapitel 3
behandelten Modellen konsistent sind. Die Entsprechungen sind in Tabelle 14 aufgelistet:
Tabelle 14: Zuordnung der Bezeichnungen
Schaltplan
brr
trr
Rrr
Rsn0
Rsn
brsn
trr2
Vj
Text
 rr
 HL
Rrr
RM0
RM
 rsn
 fr
Ve
Schaltplan
Vrsn
Ij
Icj
Ifw
Irr
Ibd
Ic0
Cj
Text
VRM
Ij
Ie
IF
IR
IBD
nsn*
Cj
In der algebraischen Schleife zur Berechnung von Ifw aus Vj ist ein zusätzliches
Verzögerungsglied eingesetzt. Damit wird die numerische Stabilität des Modells
verbessert. Ohne dieses Verzögerungsglied treten leicht Konvergenzprobleme auf. Die
Zeitkonstante dieses Gliedes ist so klein, dass ihr Einfluss auf die Simulationsergebnisse
vernachlässigt werden darf.

Koninklijke Philips Electronics N.V. 2009
79
PR-TN 2009/00487
A.2.2
Unclassified
Vergleich von Messungen und Simulationen
Abbildung 58: Reverse-Recovery bei 25°C
Abbildung 59: Reverse-Recovery bei 125 °C
80

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 60: Forward-Recovery bei 25 °C
Abbildung 61: Forward-Recovery bei 125 °C

Koninklijke Philips Electronics N.V. 2009
81
PR-TN 2009/00487
Unclassified
Abbildung 62: Reverse-Recovery bei 25 °C
Abbildung 63: Reverse-Recovery bei 125 °C
82

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildung 64: Forward-Recovery bei 25 °C
Abbildung 65: Forward-Recovery bei 125 °C

Koninklijke Philips Electronics N.V. 2009
83
PR-TN 2009/00487
Unclassified
Abkürzungsverzeichnis
ADE
MLCC
PCB
RLZ
84
Ambipolare Diffusionsgleichung
Mehrschicht-Keramik-Kondensator
Printed Circuit Board
Raumladungszone

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Symbolverzeichnis
n
p
 rr
 rsn

0
0
n
p

 eff
 fr
 HL
n
p

Dn
Dn
E
Eaus
Eein
Ekrit
fBW
fknee
IDstat
ID
ID
inDiff
inFeld
in
ipDiff
ipFeld
ip
Irr
IR
Is
La
n
n0
nA
mittlere Elektronenkonzentration im Mittelgebiet
Mittlere Löcherkonzentration im Mittelgebiet
Modellparameter, der die Höhe der Rückstromspitze bestimmt
Modellparameter, der den Verlauf der Einschaltspannungsüberhöhung beeinflusst
relative Permittivität
elektrische Feldkonstante
magnetische Feldkonstante
Elektronenbeweglichkeit
Löcherbeweglichkeit
Raumladungsdichte
Zeitkonstante beim Abklingen des Stroms nach Erreichen der Rückstromspitze
Modellparameter, der den Verlauf der Einschaltspannungsüberhöhung beeinflusst
Modellparameter, Ladungsträgerlebensdauer bei starker Injektion
Lebensdauer der Elektronen bei schwacher Injektion
Lebensdauer der Löcher bei schwacher Injektion
Potential
Diffusionskoeffizient für Elektronen
Diffusionskoeffizient für Löcher
elektrische Feldstärke
Verlustenergie bei einem Ausschaltvorgang
Verlustenergie bei einem Einschaltvorgang
kritische Feldstärke
Messgerätbandbreite
Kniefrequenz
Diodenstrom vor dem Abschalten
Diodenstrom
Diodenvorwärtsstrom
Diffusionsstromdichte der Elektronen
Feldstromdichte der Elektronen
Stromdichte der Elektronen
Diffusionsstromdichte der Löcher
Feldstromdichte der Löcher
Stromdichte der Löcher
Höhe der Rückstromspitze
Diodenrückstrom
Sättigungsstrom
Ambipolare Diffusionslänge
Elektronenkonzentration
Elektronenkonzentration im thermodynamischen Gleichgewicht
Konzentration ionisierter Akzeptorstörstellen
Koninklijke Philips Electronics N.V. 2009
85
PR-TN 2009/00487
nD+
ni
nn
np
p
p0
pn
pp
QC
qe
qm
Qrr
R
RM0
RM
Rrr
Tm
VDSS
VD
Ve
VFRM
VRmax
VRM
VR
VT
W
w
86
Unclassified
Konzentration ionisierter Donatorstörstellen
intrinsische Ladungsträgerdichte
Elektronenkonzentration im N-Gebiet
Elektronenkonzentration im P-Gebiet
Löcherkonzentration, Defektelektronenkonzentration
Löcherkonzentration im thermodynamischen Gleichgewicht
Löcherkonzentration im N-Gebiet
Löcherkonzentration im P-Gebiet
Ladung der Sperrschichtkapazität
Ladung am Rand des Mittelgebietes
Ladung im Mittelgebiet
Reverse-Recovery-Ladung
Rekombinationsüberschuss
Modellparameter, Bahnwiderstand des Mittelgebietes bei sperrender Diode
Bahnwiderstand des Mittelgebietes
Modellparameter, mit dem aus dem Diodenrückstrom die Sperrschichtspannung
berechnet wird
Diffusionszeit der Ladungsträger durch das Mittelgebiet
Maximale Sperrspannung eines Mosfets
Diodenspannung
Spannung an der Sperrschicht
Einschaltspannungsüberhöhung
Maximale Sperrspannung
Spannung über dem Mittelgebiet
Sperrspannung an der Diode
Temperaturspannung
Rekombinationsrate
Breite des schwach dotierten Mittelgebietes

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Abbildungsverzeichnis
Abbildung 1: PN-Übergang im thermischen Gleichgewicht [16]
Abbildung 2: Potential-, Feldstärke- und Raumladungsverlauf am PN-Übergang für
unterschiedliche Dotierungsprofile [16]
Abbildung 3:Konzentrationsanhebung bei Durchlassbelastung[16]
Abbildung 4: Stromübernahme durch Rekombination [16]
Abbildung 5: Konzentrationsverteilung bei starker Injektion [16]
Abbildung 6: Schematische Darstellung von Lösungen der ambipolaren Diffusionsgleichung
Abbildung 7: Typische Kennlinie einer PSN-Diode [16
Abbildung 8: Begrenzung der maximalen Sperrspannung einer PSN-Diode [16]
Abbildung 9: Rückgang der Ladungsträgerkonzentration [16]
Abbildung 10: Typischer Verlauf des Reverse-Recovery-Stroms
Abbildung 11: Konzentrationsverlauf beim Erreichen der Rückstromspitze
Abbildung 12: Konzentrationsverlauf nach dem Einschalten [16]
Abbildung 13: Mögliche Klassifizierung von Modellansätzen
Abbildung 14: Anordnung der Ladungsknoten
Abbildung 15: Topologie eines Tiefsetzstellers
Abbildung 16: Ladungsträgerabbau während Reverse-Recovery
Abbildung 17: Reverse-Recovery im Charge-Control-Konzept
Abbildung 18: Forward-Recovery im Charge-Control-Konzept
Abbildung 19: Clamped-Inductive-Load Testschaltung
Abbildung 20: Strom- und Spannungsverlauf während eines Messdurchlaufs
Abbildung 21: Überlagerungsprinzip während eines Schaltvorgangs
Abbildung 22: Anordnung zur Minimierung der Streuinduktivität
Abbildung 23: Mögliche Messanordnung 1
Abbildung 24: Mögliche Messanordnung 2
Abbildung 25: Messschaltung, Ansicht von oben
Abbildung 26: Messschaltung, Ansicht von unten
Abbildung 27: Begrenzung der Diodenvorwärtsspannung durch Mosfet (blau: VD, rot:
ID, grün: VD aus fehlerfreier Messung)
Abbildung 28: Diodensamples (v.l.n.r.: Diode A, C, B, D)
Abbildung 29: Messung der statischen Kennlinien
Abbildung 30: Statische Kennlinien
Abbildung 31: Vergleich der statischen Kennlinien bei 25°C (links) und 100°C (rechts)
Abbildung 32: Reverse-Recovery-Verhalten bei verschiedenen Durchlassströmen
Abbildung 33: Reverse-Recovery-Verhalten aller Dioden im Vergleich
Abbildung 34: Reverse-Recovery-Verhalten bei verschiedenen Stromsteilheiten
Abbildung 35: Ausschaltenergien der Dioden in Abhängigkeit von der Stromsteilheit
Abbildung 36: Reverse-Recovery-Verhalten bei verschiedenen Temperaturen
Abbildung 37: Forward-Recovery-Verhalten bei verschiedenen Durchlassströmen
Abbildung 38: Forward-Recovery-Verhalten aller Dioden im Vergleich
Abbildung 39: Forward-Recovery-Verhalten bei verschiedenen Stromsteilheiten
Abbildung 40: Forward-Recovery-Verhalten bei verschiedenen Temperaturen
Abbildung 41: Frequenzabhängige Gesamtverluste der Dioden

Koninklijke Philips Electronics N.V. 2009
87
PR-TN 2009/00487
Unclassified
Abbildung 42: Gemessenes Rechtecksignal
Abbildung 43: Modellgrundstruktur
Abbildung 44: Implementierung des statischen Verhaltens
Abbildung 45: Berechnung der mittleren Ladungsträgerkonzentration im Mittelgebiet
Abbildung 46: Realisierung des Reverse-Recovery-Verhaltens
Abbildung 47: Berechnung des Forward-Recovery-Widerstandes
Abbildung 48: Reverse-Recovery bei 25 °C
Abbildung 49: Reverse-Recovery bei 125 °C
Abbildung 50: Forward-Recovery bei 25 °C
Abbildung 51: Forward-Recovery bei 125 °C
Abbildung 52: Messschaltung Top Layer
Abbildung 53: Messschaltung Bottom Layer
Abbildung 54: Begrenzung des Rückstroms
Abbildung 55: Bestimmung des Laufzeitunterschiedes zwischen AP033 und PP007
Abbildung 56: Untersuchung der Testschaltung auf parasitäre Kapazitäten
Abbildung 57: Untersuchung des Shuntwiderstands auf induktive Anteile
Abbildung 58: Reverse-Recovery bei 25°C
Abbildung 59: Reverse-Recovery bei 125 °C
Abbildung 60: Forward-Recovery bei 25 °C
Abbildung 61: Forward-Recovery bei 125 °C
Abbildung 62: Reverse-Recovery bei 25 °C
Abbildung 63: Reverse-Recovery bei 125 °C
Abbildung 64: Forward-Recovery bei 25 °C
Abbildung 65: Forward-Recovery bei 125 °C
88

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
Tabellenverzeichnis
Tabelle 1: Verwendete Mosfets
Tabelle 2: Untersuchte Dioden (Anmerkung zur Reverse-Recovery-Zeit: IF=0,5A über
Irr=1A auf IR=0,25A)
Tabelle 3: Reverse-Recovery-Ladung Qrr in nC bzw. Sperrschichtladung QC in nC bei
verschiedenen Durchlassströmen
Tabelle 4: Ausschaltverlustenergie Eaus in uJ bei verschiedenen Durchlassströmen
Tabelle 5: Reverse-Recovery-Ladung Qrr in nC bei verschiedenen Stromsteilheiten
Tabelle 6: Ausschaltverlustenergien Eaus in uJ bei verschiedenen Stromsteilheiten
Tabelle 7: Reverse-Recovery-Ladung Qrr in nC bei verschiedenen Durchlassströmen und
Temperaturen
Tabelle 8: Ausschaltverlustenergien Eaus in uJ bei verschiedenen Durchlassströme und
Temperaturen
Tabelle 9: Vergleich der auftretenden Einschaltspannungsüberhöhungen VFRM in V
Tabelle 10: Einschaltverlustenergien Eein in uJ bei verschiedenen Durchlassströmen
Tabelle 11: Einschaltverlustenergien Eein in uJ bei verschiedenen Stromsteilheiten
Tabelle 12: Einschaltverlustenergien Eein in uJ bei verschiedenen Durchlassströmen und
Temperaturen
Tabelle 13: Parametrisierung des Modells für die vermessenen Dioden
Tabelle 14: Zuordnung der Bezeichnungen

Koninklijke Philips Electronics N.V. 2009
89
PR-TN 2009/00487
Unclassified
Literaturverzeichnis
(1) P. Antognetti and G. Massobrio. Semiconductor Devices Modeling with SPICE.
McGraw-Hill, New York, 1988.
(2) F. Bertha, B. Velaerts, P. Mathys, E. Tatakis, A. Wyns, D. Bogaerts, and M.
Miller. An improved power diode model for pspice, applied to converter
simulation. In Power Electronics and Applications, 1993., Fifth European
Conference on, pages 249-254 vol.2, Sep 1993.
(3) J. Catt. An improved method for ultra fast recovery diode testing. In Applied
Power Electronics Conference and Exposition, 1994. APEC '94. Conference
Proceedings 1994., Ninth Annual, pages 473-479 vol.1, Feb 1994.
(4) M. Cotorogea. Implementation of mathematical models of power devices for
circuit simulation in pspice. In Computers in Power Electronics, 1998. 6th
Workshop on, pages 17-22, 1998.
(5) R.B. Darling. A full dynamic model for pn-junction diode switching transients.
Electron Devices, IEEE Transactions on, 42(5):969-976, May 1995.
(6) R.W. Erickson. EMI and Layout Fundamentals for Switched-Mode Circuits.
ECCE, University of Colorado at Boulder, 2009.
(7) B. Fatemizadeh, P.O. Lauritzen, and D. Siber. Modeling of power
semiconductor devices, problems, limitations and future trends. In Computers in
Power Electronics, 1996., IEEE Workshop on, pages 120-127, Aug 1996.
(8) J Hancock and P. Kasenbacher. Messen mit der richtigen Bandbreite. Aktuelle
Technik, (7):30-32, 2007.
(9) R. Kraus, K. Hoffmann, and H.J. Mattausch. A precise model for the transient
characteristics of power diodes. In Power Electronics Specialists Conference,
1992. PESC '92 Record., 23rd Annual IEEE, pages 863-869 vol.2, Jun-3 Jul
1992.
(10) P.O. Lauritzen and C.L. Ma. A simple diode model with reverse recovery.
Power Electronics, IEEE Transactions on, 6(2):188-191, Apr 1991.
(11) Y.-C. Liang and V.J. Gosbell. Diode forward and reverse recovery model for
power electronic spice simulations. Power Electronics, IEEE Transactions on,
5(3):346-356, Jul 1990.
(12) J.G. Linvill. Lumped models of transistors and diodes. Proceedings of the IRE,
46(6):1141-1152, June 1958.
(13) C.L. Ma and P.O. Lauritzen. A simple power diode model with forward and
reverse recovery. Power Electronics, IEEE Transactions on, 8(4):342-346, Oct
1993.
90

Koninklijke Philips Electronics N.V. 2009
Unclassified
PR-TN 2009/00487
(14) C.L. Ma, P.O. Lauritzen, and J. Sigg. Modeling of power diodes with the
lumpedcharge modeling technique. Power Electronics, IEEE Transactions on,
12(3):398-405, May 1997.
(15) H.A. Mantooth and J.L. Duliere. A unifed diode model for circuit simulation.
Power Electronics, IEEE Transactions on, 12(5):816-823, Sep 1997.
(16) Alfred Porst. Bipolare Halbleiter.
München/Heidelberg, 2nd edition, 1979.
Hüthig
&
Pflaum
Verlag,
(17) S. Schröder. Circuit-Simulation Models of High-Power Devices Based on
Semiconductor Physics. PhD thesis, RWTH Aachen, 2003. S. 40f.
(18) Cher Ming Tan and King-Jet Tseng. Using power diode models for circuit
simulations a comprehensive review. Industrial Electronics, IEEE Transactions
on, 46(3):637-645, Jun 1999.
(19) T. Vogler and D. Schröder. A new and accurate circuit-modelling approach for
the power-diode. In Power Electronics Specialists Conference, 1992. PESC '92
Record., 23rd Annual IEEE, pages 870-876 vol.2, Jun-3 Jul 1992.
(20) J. Williams and D. Beebe. Diode turn-on time induced failures in switching
regulator. Linear Technology Magazine, 19(1):34-38, March 2009.
(21) C. Winterhalter, S. Pendharkar, and K. Shenai. A novel circuit for accurate
characterization and modeling of the reverse recovery of high-power high-speed
rectifiers. Power Electronics, IEEE Transactions on, 13(5):924-931, Sep 1998.
(22) A.T. Yang, Yu Liu, and J.T. Yao. An efficient nonquasi-static diode model for
circuit simulation. Computer-Aided Design of Integrated Circuits and Systems,
IEEE Transactions on, 13(2):231-239, Feb 1994.
(23) Z. Yu, D. Chen, L. So, and R.W. Dutton. Pisces-2et -two-dimensional device
simulation for silicon and heterostructures. Technical report, Standford
University, 1994.

Koninklijke Philips Electronics N.V. 2009
91