Folie 38. Zahlkörper C und Polynome über C
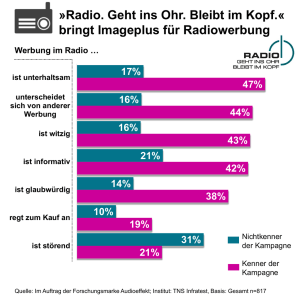
Werbung

Folie 38. Zahlkörper C und Polynome über C
10.01.01 P.Vachenauer
Der Körper C der komplexen Zahlen
2
2
C = {x + iy ; x, y ∈ R ∧ i = – 1} ist Zerfällungskörper von x + 1 ∈ R [ x ]
Bezeichnungen und Rechenregeln
imaginäre Einheit
2
i mit i = – 1
komplexe Zahl
z = x + iy mit x, y ∈ R
Realteil von z
Re (z) = x
Imaginärteil von z
Im (z) = y
konjugiert komplexe Zahl zu z
z = x – iy
Betrag von z
2
z = x + iy =
2
z⋅z
x +y =
Argument von z
arg z := ϕ , sodass gilt
Polardarstellung von z
z = z ( cos ϕ + i sin ϕ )
Addition
( a + ib ) + ( c + id ) = ( a + c ) + i ( b + d )
Multiplikation
( a + ib ) ( c + id ) = ( ac – bd ) + i ( ad + bc )
( cos ϕ + i sin ϕ ) ( cos ψ + i sin ψ ) =
= cos ( ϕ + ψ ) + i sin ( ϕ + ψ )
Division
a + ib
( a + ib ) ( c – id )
ac + bd bc – ad
-------------- = -------------------------------------- = ------------------ + i ------------------ ,
c + id
( c + id ) ( c – id )
c2 + d2
c2 + d2
falls c + id ≠ 0
Modell
y
Die Gauss-Zahlenebene
Die Zahl z = x + iy entspricht dem Punkt ( x, y )
i
x + iy
|z|
in der Ebene. Multiplikation mit i bedeutet eine
Drehung um 90° :
ϕ
1
i ( x + iy ) = – y + ix .
x
x
x - iy
Weitere Rechenregeln
z⋅w = z ⋅ w
zn = z n
arg ( z ⋅ w ) = arg ( z ) + arg ( w )
arg ( z n ) = n ⋅ arg ( z )
z⋅w = z ⋅ w
zn = ( z )n
Definition
a) M heißt Zerfällungskörper des Polynoms p über dem Körper K , wenn p
über M in Linearfaktoren zerfällt: p = a n ( x – b 1 ) ( x – b 2 )… ( x – b n ) , b k ∈ M
b) M heißt algebraisch abgeschlossen, wenn jedes nichtkonstante Polynom
über M in Linearfaktoren zerfällt.
Als Vektorraum über K hat M die Dimension m mit
1 ≤ m ≤ n! .
Zwei einfache Spezialfälle
1) K = R : Dann ist stets m ≤ 2 und M = C ( → (a) unten )
2) K = Zp : Dann ist stets m ≤ n ( → Folie 39)
4 weitere Grundregeln für Polynome über C
(a) Der Fundamentalsatz der Algebra (Gauss 1799 im Alter von 22 Jahren)
C ist algebraisch abgeschlossen, d.h. jedes nichtkonstante Polynom mit Koeffizienten
aus C zerfällt in C in Linearfaktoren
(b) Reelle Polynome haben reelle oder paarweise konjugiert komplexe Nullstellen
Beispiel
2
3
2
x + 1 = ( x + 1 ) ( x – x + 1 ) = ( x + 1 ) ( x – 1--2- ) + 3--4-
= ( x + 1 ) ( x – 1--2- – i 1--2- 3 ) ( x – 1--2- + i 1--2- 3 )
(c) Rationale Nullstellen (Gauss)
n
Hat das Polynom p = a n x + … + a 1 x + a 0 ganzzahlige Koeffizienten, so gilt
a, b ∈ Z , a, b teilerfremd , p a--- = 0 ⇒ a teilt a 0 und b teilt a n in Z
b
(d) Nullstellendarstellung mit Wurzelausdrücken
Grad p = 2 :
2
1
b 1, 2 = --------- – a 1 ± a 1 – 4a 2 a 0 ,
2a 2
Grad p = 3,4 : Formeln von Cardano (Springers Mathematische Formeln S. 64)
Grad p > 4 :
I.a. nicht möglich (Abel 1829)
Carl Friedrich Gauss
1777 - 1855
Göttingen
Niels Hendrik Abel
1802 - 1829
Norwegen