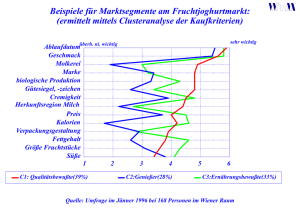
Kap. 5 Spatial (räumliches) Data Mining

Kap. 5
Spatial (räumliches) Data Mining
Univ.-Prof. Dr.-Ing. Wolfgang Reinhardt
AGIS / Inst. Für Angewandte Informatik (INF4)
Universität der Bundeswehr München
[email protected]
www.agis.unibw.de
Überblick / Ziele
• Einführung Data Mining / Spatial Data Mining
(sp. DM)
• Clusteranalyse als wesentliche Methode des sp.
DM
• Anwendungsbeispiel
 Kennen der Methoden / Einschätzung der
Anwendbarkeit
2 / 50
Data Mining
Unter Data Mining („Daten-Bergbau, DatenSchürfen“), sinngemäß „in einem Datenberg
nach wertvollem Wissen suchen“, versteht
man die systematische Anwendung
statistischer (u.a.) Methoden auf einen
Datenbestand mit dem Ziel, neue Muster zu
erkennen. Hierbei geht es auch um die
Verarbeitung sehr großer Datenbestände,
wofür effiziente Methoden benötigt werden
…
(Abgeändert nach wikipedia)
3 / 52
Data Mining
SRC.: http://winfwiki.wifom.de/index.php/Data_Mining_%E2%80%93_Anwendungsfelder_und_%E2%80%93beispiele
4 / 52
Spatial Data Mining
Spatial data mining (auch: KDD - knowledge
discovery in spatial databases)
Bezieht sich darauf implizit vorhandene
Informationen, Beziehungen, räumliche
Strukturen etc. in raumbezogenen
Datenbeständen zu ermitteln (die nicht
explizit gespeichert sind)
5 / 52
Spatial Data Mining
Das klassische Beispiel
Infizierte Wasserpumpe?
Dr. John Snow, Untersuchung
der Ursachen einer
Choleraepidemie London,
September 1854
Krankheitshäufung
6 / 52
Lösung durch Räumliche Analyse
Räumliche Beziehungen von Objekten
einer Art sind dargestellt (Todesfälle)
Räumliche Beziehung zu
Objekten anderer Arten sind
dargestellt (Wasserpumpen)
Es ist nicht nur wichtig
wo ein Cluster ist –
sondern auch was
sonst dort ist (z.B.
Wasserpumpen)!
7 / 52
Ziele des Spatial Data Mining
• Räumliche Cluster erkennen
• Objekte erkennen, die solche Cluster
möglicherweise verursachen
• Information extrahieren, die für
die Erklärung der Cluster relevant
ist (und irrelvante Information
wegfiltern)
• Information so präsentieren, daß der Nutzer
sein Anwendungswissen in die Analyse
einbringen kann
8 / 52
Ansatz für Spatial Data Mining
Data Mining
Geoinformation / Methoden
Spatial Data Mining
9 / 52
Besonderheiten des Spatial Data Mining
• Raumbezogene Daten (Raumbezug /
weitere Attribute)
• Räumliche (u.a.) Beziehungen zw. Objekten
• Geometrische
• Topologische
• (vgl. Kap. 3 und 4)
• Konsequenz: spatial data mining deutlich
komplexer als data mining
10 / 52
Kurze Einführung, spatial data mining
CLUSTERANALYSEN
11 / 52
Data Mining
Typische Aufgabenstellungen





Klassifizierungsanalysen
Segmentierungsanalysen
Prognoseanalysen (-> Zeit)
Abhängigkeitsanalysen
Abweichungsanalysen
12 / 52
Data Mining
Klassifizierung
 Objekte werden einer vorher bestimmten Klasse
zugeordnet
 Zuordnung findet aufgrund der Parameter und
der Klasseneigenschaften statt
 Anzahl an Klassen i.d.R. bekannt
 Informationen sind vorab bekannt
Segmentierung
 Objekte werden in Gruppen zusammengefasst,
welche vorher nicht bekannt sind
 Anzahl an Gruppen zu Beginn i.d.R. unbekannt
 Datenabhängige Einteilung  objektiv
nachvollziehbar und reproduzierbar
13 / 52
Data Mining
Das am Häufigsten verwendete Verfahren der
Segmentierung ist die Clusteranalyse
Definition (Steinhausen und Langer, 1977):
 Clusteranalyse steht „für eine Reihe
unterschiedlicher mathematisch-statistischer und
heuristischer Verfahren, deren Ziel darin besteht,
eine meist umfangreiche Menge von Elementen
durch Konstruktion homogener Klassen, Gruppen
oder Cluster optimal zu strukturieren“.
14 / 52
Spatial data mining
Bei räumlichen Daten spielt deren Lage zueinander
eine große Rolle. -> Clusteranalyse
Aber auch die Untersuchung der räumlichen Verteilung
- sind Objekte gebündelt (clustered) oder verstreut
(dispersed)- ist von Interesse:
15 / 52
Räumliche Verteilung von Objekten
Einbeziehen des Nutzers
 Visualisierung
 Kontext!
16 / 52
Räumliche Verteilung von Objekten
Frage: Sind die Standorte zufällig verteilt?
Kriterium?
17 / 52
Räumliche Verteilung von Objekten
Frage: Sind die Standorte zufällig verteilt?
Abstand / Distanz zum nächsten Nachbarn (und deren Verteilung)
Siehe Literatur
18 / 52
Räumliche Verteilung von Objekten
Weitere Verfahren zur Ermittlung des Grades der räumlichen
Verteilung: Verschiedene auf räumliche Autokorrelation
beruhende Maße kommen zum Einsatz.
Beispiel: Ripley k-function K(t), wird benutzt für:
• Beschreibung des Musters eines Punkthaufens
• Hypothesen über die Verteilung des Punkthaufens zu testen
Beispiel: Test ob ein Punkthaufen rein zufällig verteilt ist
(CSR: Complete spatial randomness), durch K(t) für einen
homogenen Poisson Prozess:
t – Distanz zwischen Punkten
19 / 52
Räumliches Verteilung von Objekten
Beispiel: Standorte verschiedener Spezies gegeben, sind diese zufällig verteilt?
Src.: http://www.spatial.cs.umn.edu/paper_list.html
Answers:
and
20 / 52
Räumliche Verteilung von Objekten
Test der räumlichen Verteilung:
K function
Abweichung!
Abstand t
21 / 52
Räumliche Verteilung von Objekten
Cluster?
Auffinden räumlicher Strukturen -> Clusteranalyse
http://www.biostat.umn.edu/~dipankar/pubh8472/RipleysK.pdf
22 / 52
Clusteranalyse
Grundidee:
Eine heterogene Gesamtheit von „Fällen“ (Personen/Objekte)
soll in homogene Gruppen oder Cluster aufgeteilt werden
Dabei wird die Ähnlichkeit der Fälle auf allen relevanten
Variablen berücksichtigt
Zentrale Fragen:
• Wie wird die Ähnlichkeit von Fällen bestimmt?
• Welche Parameter werden ausgewählt?
• Wie wird die Gruppenaufteilung vorgenommen, wenn
die Ähnlichkeit zwischen Fällen bekannt ist?
23 / 52
Clusteranalyse
Objekte innerhalb eines Clusters sollen möglichst
ähnlich sein (Homogenität in den Clustern)
räumlich: möglichst geringer Abstand der Objekte
und ggfs. weiterer Parameter
Cluster zueinander sollen möglichst unähnlich sein
(Heterogenität zwischen den Clustern), räumlich:
möglichst großer Abstand der Cluster)
24 / 52
Bestimmung der Ähnlichkeit
Quantifizierung der Ähnlichkeiten zwischen den in der
Clusteranalyse berücksichtigten Objekten durch eine
statistische Maßzahl
Ähnlichkeitsmaße
 Drücken die Ähnlichkeit zwischen zwei Objekten aus
 Ein großer Wert beschreibt eine hohe Ähnlichkeit
Distanzmaße
 Drücken die Unähnlichkeit zwischen zwei Objekten aus
 Ein großer Wert beschreibt eine niedrige Ähnlichkeit
 Bei identischen Objekten ist die Distanz Null
Maße: abhängig von Skalen (binär, ordinal, metrisch …)
25 / 52
Bestimmung der Ähnlichkeit
Hinweis:
 Clusteranalyse erfordert kein spezielles
Skalenniveau (nominal, metrisch …)
 Thema dieser Vorlesung ist Geoinformatik, daher
Konzentration auf metrische Skalen
26 / 52
Distanzmaße
Werden hauptsächlich bei quantitativen
Parametern verwendet (metrische Skalen)
Die am häufigsten verwendeten basieren auf der
Minkowski-Metrik
r = 1  City-Block-Metrik
r = 2  Euklidische Distanz
…
27 / 52
Ablauf der Clusteranalyse
Analyse und Präzisierung der Fragestellung
Modifikation, Korrektur
Auswahl der Parameter, Aufstellen der Matrix
Bestimmung der Ähnlichkeit
Bestimmung der Clusteranzahl
Auswahl des Algorithmus
Durchführung
Analyse/Bewertung der Ergebnisse
28 / 52
Auswahl der Parameter
Clusteranalyse erfordert kein spezielles
Skalenniveau (nominal, metrisch …)
Wahl der Parameter muss dem Ziel der
Analyse gerecht werden, beachten:
 Wahl von zu vielen Parametern  viele Cluster,
die sich weiter zusammenfassen ließen
 Wahl von zu wenigen Parametern  wenige
Cluster, die sich weiter ausdifferenzieren ließen
Gute Auswahl der Parameter = einfaches
und leicht verständliches Clusterergebnis
Schlechte Auswahl der Parameter =
komplexes Clusterergebnis, dessen wahre
Struktur oft schwierig oder unmöglich zu
erkennen ist
29 / 52
Auswahl der Parameter – 2 räumliche Beispiele
Beispiel 1, gegeben n Standorte (Punkte)
Gesucht (Fragestellung):
K Cluster von „benachbarten“ Standorten
-> univariate Clusteranalyse (u CA)
Beispiel 2, gegeben n Vektoren
Gesucht (Fragestellung): Cluster von Vektoren mit
„ähnlicher“ Richtung und Länge,
die benachbart sind
-> multivariate Clusteranalyse (m CA)
U CA rel. einfach, Betrachtung m CA im weiteren
30 / 52
Aufstellen der Rohdatenmatrix (m CA)
Aufstellen der Rohdatenmatrix (Beispiel)
 Objekte
 Parameter
Parameter
Vektor
1 Vektor
2 Vektor
Vektor
1 Vektor
2 Vektor
3 ...3
Geeignete Normierung
der Werte!
VektorVektor
n
n
Z 
ij
X [m]
249,7211,562
240,0351,673245,546
1,757
...
242,098
1,604
Y [m]
549,2720,856
548,2721,923562,186
0,968
...
536,249
-0,065
20,883 1,499
20,883 1,49920,883...
Länge [m] 1,499
14,8040,315
Richtung [°]-2,423
...
204,137-2,423
203,137-2,423
204,136
-0,640
267,832
X X
S
ij
i
31 / 52
i
Normierung
32 / 52
Gruppenbildung: Methoden der Clusteranalyse
Cluster-Algorithmen
Partitionierend
K-means
Minimal Spanning
Tree
Hierarchisch
Single Linkage
s. z.B. Malczewski, J., 2006: GIS-based multicriteria decision analysis: a survey of the literature,
IJGIS (20), S 703-726.
Complete Linkage
33 / 52
Partitionierende Clustermethoden
Gehen von einer gegebenen
Startgruppierung aus
Die Startgruppierung muss vom Nutzer
geschätzt werden
Alle Objekte werden zu Beginn einem Cluster
zugeordnet
Prominentes Beispiel: K-Means
1. Festlegung von K Cluster-Mittelpunkten.
2. Zuordnen der Werte zu dem am nächsten liegenden Mittelpunkt.
3. Neuberechnung der Cluster-Mittelpunkte.
4. Prüfen, ob das Konvergenz-Kriterium, welches zu Beginn festgelegt
wurde, erfüllt ist.
34 / 52
Methoden der Clusteranalyse – k-means
Festzulegende Parameter: Anzahl Cluster = 3
Gewählte Mittelpunke: P9, P84, P106
(aus den geg. Punkten)
35 / 52
Methoden der Clusteranalyse – k-means
P7
P8
P9
P81
P82
P84
P106
P107
M1= K106
34,85
21,36
28,58
13,67
8,06
24,36
0
6,77
M2 = K9
32,89
0,85
0
3,17
12,05
1,62
28,52
19,17
M3 = K84
42,57
2,66
1,62
1,81
6,58
0
24,36
21,07
Berechnete Distanzwerte der Punkte zu den Anfangs gewählten Mittelpunkten
Hinweis: Die Distanzwerte der Punkte (Ki) sind aus den versch. Parametern (s. Folie 29) berechnet
36 / 52
Methoden der Clusteranalyse – k-means
• Iterative Berechnung neuer Mittelpunkte
• Neue Zuordnung der Punkte zu clustern
37 / 52
Methoden der Clusteranalyse – k-means
Ergebnis hängt sehr stark von der Wahl der AnfangsCluster-Mittelpunkte ab
Ergebnis bei Wahl von anderen Anfangsmittelpunkten!
Quelle: M. Reus (2010), Diplomarbeit (unveröffentlicht)
Weiteres und Anwendungsbeispiel:
Nuhn, Eva; Kropat, E.; Reinhardt, Wolfgang; Pickl, S. (2012): Preparation of Complex
Landslide Simulation Results with Clustering Approaches for Decision Support and Early
Warning. hicss, pp.1089-1096, 2012 45th Hawaii International Conference on System
38 / 52
Sciences.
Methoden der Clusteranalyse - hierarchisch
Hierarchisches Vorgehen, keine Vorabwahl der Anzahl der Cluster
• Erstellen einer Ähnlichkeits-Matrix mit den Abständen der
einzelnen Cluster zueinander (zu Beginn ist jeder Punkt ein cluster)
• Zusammenfassen der Cluster nach geg. Kriterien (s.u)
• Update der Ähnlichkeits-Matrix
• Iteration bis Abbruch-Kriterium erfüllt ist
A
B
C
D
A
0
1
6
7
B
C
D
Geringster Abstand
A/B C
0
5
8
0
2
0
A/B 0
C 5
D 7
Ähnlichkeitsmatrix zu Beginn (li) und nach 1.Fusion (re)
39 / 52
0
2
D
0
Methoden der Clusteranalyse - hierarchisch
Single Linkage (SL) / Complete Linkage (CL)
http://de.wikipedia.org/wiki/Hierarchische_Clusteranalyse
Dendrogramm für single-linkage
Kriterium für Fusionen:
Sl: Minimaler Abstand aller Elementpaare aus den beiden Clustern
Cl: Maximaler Abstand aller Elementpaare aus den beiden Clustern
40 / 52
Methoden der Clusteranalyse - hierarchisch
Vorteil für Single Linkage / complete linkage:
- keine Vorabwahl der Anzahl der Cluster
Single Linkage kann zu Längliche, kettenförmige Cluster
führen
Vorteil für complete linkage: Eher kompakte Cluster
41 / 52
Kurze Einführung, spatial data mining
ANWENDUNGSBEISPIEL
42 / 52
Forschungsprojekt „EGIFF“
Motivation
Verbundprojekt EGIFF
(“Geotechnologien”, BMBF/DFG)
Testgebiet
Teilprojekt: “Entwicklung eines
gekoppelten Simulations- und
Informationssystems”
Aufbereitung, Analyse und
Visualisierung der komplexen
Simulationsergebnisse mit Hilfe
von Spatial Data Mining Methoden
https://www.unibw.de/inf4/professuren/geoinformatik/forschung/projektauswahl/slide
43 / 52
Bruchentwicklung im SIMS
44 / 52
Ergebnis: Verschiebungen der Knoten
45 / 52
Simulationsergebnisse
FE-Netz
Clusterbildung
Verschiebungsvektoren (Sehr große Datenmenge, Millionen von Vektoren)
46 / 52
Aufbereitung der Simulationsergebnisse
Segmentierung der Verformungsbereiche:
 Methoden der Clusteranalyse
Bestimmung des Rutschkörpers
Simulationsergebnisse für den
Rutschkörper
47 / 52
Methoden der Clusteranalyse
2D:
- Lage
- Richtung
- Länge
3D:
- Ähnlichkeitsmaße
- Lage
- Distanzmaße
- Azimuth, Inklination
- Länge
Analyse und Präzisierung der Fragestellung
Auswahl der Elemente und Variablen
Wahl eines Proximitätsmaßes
Bestimmung des Algorithmus
SF / CF
Bestimmung der Clusteranzahl
Standardisierung:
Technische Durchführung
Z 
ij
Analyse der Ergebnisse
X X
S
ij
i
d  ( a  b )²  (a  b )²  ...  ( a  b )² 
1
1
2
2
n
n
( X  X )²  (Y  Y )²  ( L  L )²  ( R  R )²
1
2
1
2
1
2
1
2
48 / 52
i
Anwendung Clusteranalyse
Analyse und Präzisierung der Fragestellung
Auswahl der Elemente und Variablen
Wahl eines Proximitätsmaßes
Bestimmung des Algorithmus
Bestimmung der Clusteranzahl
Technische Durchführung
- Subjektive Methoden
- Objektive Methoden
Stopping Rule von Mojena
Analyse der Ergebnisse
49 / 52
Anwendung Clusteranalyse
Multivariate Clusteranalyse
(X,Y,L,R)
 Einfluss der Lage zu groß!
d  (a  b )²  (a  b )²  ...  (a  b )² 
1
1
2
2
n
n
( X  X )²  (Y  Y )²  ( L  L )²  ( R  R )²
1
2
1
2
1
2
1
2
-> einige Tests erforderlich, -> Heuristik
50 / 52
Anwendung Clusteranalyse
Bivariate Clusteranalyse mit Nachbarschaftsbetrachtung (nicht
verbundene Clusterteile)
d  (a  b )²  (a  b )²  ...  (a  b )² 
1
1
2
2
n
( L  L )²  ( R  R )²
1
2
1
2
Bivariate Clusteranalyse nach Länge und
Richtung
Nachbarschaftsbetrachtung
51 / 52
n
Grundlage für Decision Support
52 / 52
Clusteranalysen
• Sehr gute Möglichkeit Daten aufzubereiten,
verständlich zu machen, zusätzliche
Information zu generieren etc.
• Allerdings erfordert der Einsatz viel
Verständnis der Anwendung
• Lösung meist iterativ zu erarbeiten
53 / 52
Vielen Dank für die Aufmerksamkeit!
Weitere Fragen?
54 / 52