9.3 Traversieren und Suchen

9.3 Traversieren und Suchen
Vor.:
Von einer „Wurzel“ w aus seien alle Ecken erreichbar
Def.:
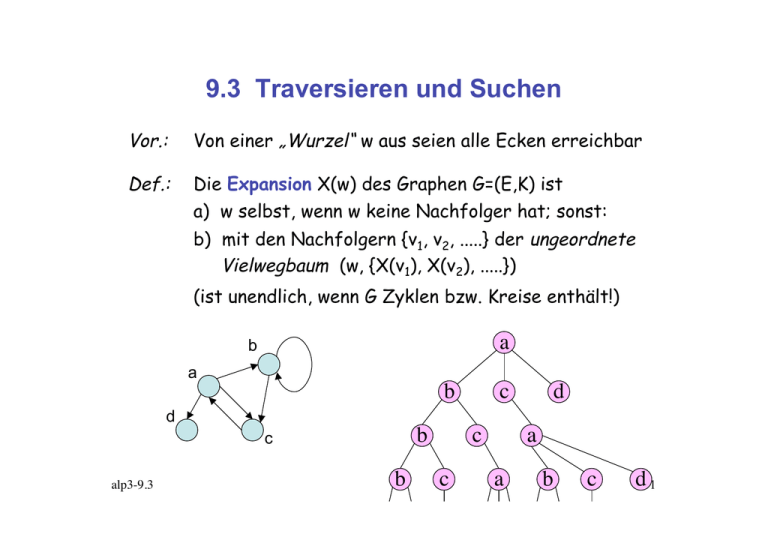
Die Expansion X(w) des Graphen G=(E,K) ist
a) w selbst, wenn w keine Nachfolger hat; sonst:
b) mit den Nachfolgern {v1, v2, .....} der ungeordnete
Vielwegbaum (w, {X(v1), X(v2), .....})
(ist unendlich, wenn G Zyklen bzw. Kreise enthält!)
a
b
a
b
c
d
d
b
c
alp3-9.3
b
c
c
a
a
b
c
d1
9.3.1 Tiefendurchlauf
Def.:
Tiefendurchlauf von G ab w = Durchlauf von X(w)
in Präordnung mit Ignorierung von Unterbäumen mit
bereits besuchter Wurzel (wenn der Graph kein Baum ist!)
(Entsprechend: Tiefensuche nach Ecke mit Eigenschaft e)
Besuchte Knoten werden markiert und dadurch wiedererkannt!
a
b
a
b
c
d
d
b
c
alp3-9.3
b
c
c
a
a
b
c
d
package Graph; // all nodes should be considered
//
to form ONE graph (see 9.2.3)
// not generic - for easier presentation
public class Node {
private boolean visited;
private final Set<Node> succ = new TreeSet<Node>();
.....
// just mark all reachable nodes, no further action:
public void depthFirstTraversal(){
if(!visited) {
visited = true;
for(Node n: succ) n.depthFirstTraversal(); }
}
}
Bemerkungen:  depthFirstTraversal ist interner Iterator
 Markierung sichert auch Termination (falls Zyklen!)
alp3-9.3
 Markierung kann nach der Schleife wieder gelöscht
werden - dann aber Mehrfachbesuche (falls kein Baum)
Flexiblere Alternative:
depthFirstTraversal nicht als interner Iterator,
sondern als externer Algorithmus - typischerweise mit
Benutzung eines internen Iterators für das Durchlaufen
der Nachfolger eines Knotens:
public void iterate(Action a){
for(Node n: succ) a.act(n);
}
public interface Action {
void act(Node x);
}
alp3-9.3
4
class DepthFirst implements Node.Action {
public void act(Node n) {
traversal(n);
}
public void traversal(Node x){
if(!x.visited) {
x.visited = true;
x.iterate(this); }
}
}
Und damit new DepthFirst().traversal(start);
( visited muss public sein)
alp3-9.3
5
... und in Haskell: besuchte Ecken werden in Akkumulator memoriert
(keine Datenabstraktion):
graph = [ [...], [...], ..... ]
-- Liste von Adjazenzlisten
dft :: [Int]
->
-- Akkumulator
Anwendung:
Int
Ecke
-> [Int]
Erreichbare Ecken
dft [] root
dft list node -- erweitert list um alle
-- von node aus erreichbaren Ecken
| node `elem` list = list
-- und falls node noch nicht erfasst:
| otherwise
= foldl dft (node:list)
(graph!!node)
alp3-9.3
Zum Nacharbeiten: warum ist das korrekt?
6
9.3.2 Breitendurchlauf
Def.:
Breitendurchlauf von G ab w =
Breitendurchlauf von X(w) mit Ignorierung
von Unterbäumen mit bereits besuchter Wurzel,
typischerweise auch mit internem Iterator
Beispiel Breitensuche „nach roter Ecke“ (vgl. 6.4.4):
interface Predicate<X> { boolean holds(X x); }
breadthFirstSearch(Predicate<Node>()
{public boolean holds(Node p){
return p.colour=="red";}})
alp3-9.3
7
public Node breadthFirstSearch(Predicate<Node> p)
throws NotFound {
Queue<Node> q = new LinkedList<Node>();
q.add(this);
do{ Node n = q.remove();
if(p.holds(n)) return n;
n.visited = true;
for(Node succ: n.succ)
if(!succ.visited) q.add(succ); }
while(!q.isEmpty());
throw new NotFound();
}
alp3-9.3
8
9.3.3 Spannbäume
Def.:
Fluten eines Graphen:
Information wird von einem Startknoten
an alle (erreichbaren) Knoten weitergegeben
Das Fluten kann wahlweise mit Breiten*- oder Tiefendurchlauf
durchgeführt werden. Durch den Informationsfluss wird ein
Baum aufgespannt, der sogenannte
(Breiten- oder Tiefen-)Spannbaum (spanning tree)
*
alp3-9.3
In nichtsequentiellen Systemen - z.B. Rechnernetzen bietet sich Breitendurchlauf an!
9
b
a
d
c
a
a
b
d
d
b
c
Breiten-Spannbaum ab a
c
Tiefen-Spannbaum ab a
alp3-9.3
10
Fluten mit Tiefendurchlauf (9.3.1, S. 4/5, hier generisch):
class Flooding<T> implements Action<T> {
private T info;
public Flooding(T i) { info = i; }
public void act(Node<T> n) {
n.info = info;
flood(n);
}
public void flood(Node<T> x){
if(!x.visited) {
x.visited = true;
x.iterate(this); }
}
}
Und damit z.B.
new Flooding<String>("hi!").flood(start);
alp3-9.3
11
Def.:
Spannbaum S eines ungerichteten, gewichteten,
zusammenhängenden Graphen G:
freier Baum mit Kanten aus G und allen Ecken aus G
Def.:
minimaler Spannbaum S:
Spannbaum mit minimalen Kosten (d.h. Summe der
Kantengewichte)
Ein minimaler Spannbaum „dünnt die Kantenmenge des Graphen
so aus“, das eine möglichst große Kostenersparnis erzielt wird,
ohne dass der Graph zerfällt (9.5).
alp3-9.3
12