2 n

Lösung 6.1.1 Turing-Maschine
 Vollziehen sie die 11 Schritte der ersten Turing-Tebelle.
1,_
1,1
2,_
2,1
3,_
3,1
4,_
4,1
2,1,>
3,1,<
3,1,>
H,1,>
1,1,<
2,_,<
H,_,>
H,_,>
1
2
3
4
5
6
7
8
9
10
11
State
2
3
1
3
2
3
1
3
1
2
H
Ausgangszustand,Zeichen  Folgezustand,schreibeZeichen,Aktion
Lösung 6.1.2 Turing-Maschine
 Eingabe der
initialen
Bandinschrift
 Eingabe der
Turing-Tabelle
Zustand x Zeichen

Folgezustand x
Zeichen x Aktion
Beispiel:
1,_  1,_,>
Lösung 6.1.3 Turing-Maschine
 Aufgabenstellung
 Entwerfen Sie eine Turing-Maschine zur Multiplikation zweier natürlicher
Zahlen.
 Spezifikation
 Eingabespezifikation





Die Zahlen werden durch die entsprechende Anzahl von ‚1‘ am Band dargestellt
Zwischen den Zahlen befindet sich ein ‚x‘ am Band
Hinter der letzten Zahl ist ein =- Zeichen am Band
Das restliche Band ist mit ‚0‘ beschrieben.
Der Schreib/Lesekopf befindet sich links von der 1. Zahl.
 Ausgabespezifikation
 Das Ergebnis ist hinter dem =, durch eine entsprechende Anzahl von ‚1‘
darzustellen.
 Beispiel:
 Die zwei Zahlen 3 und 4 sind mittels eines Turing-Programmes zu
multiplizieren
Lösung 6.1.3 Turing-Maschine
 Idee:
1. Kopiere alles vor
dem =
(den 2.Multiplikator)
ans Ende
2. Mache dies für jede
1 vor dem X
(den 1.Multiplikator)
 Siehe Anhang C
SucheStart
0
SucheStart
0
R
SucheStart
1
SucheZahl2
0
R
SucheStart
X
EndZustand
X
L
SucheZahl2
1
SucheZahl2
1
R
SucheZahl2
X
Zahl2Start
X
R
Zahl2Start
1
GeheEnde
0
R
Zahl2Start
=
Mach1Aus0
=
L
GeheEnde
1
GeheEnde
1
R
GeheEnde
=
SucheNull
=
R
SucheNull
1
SucheNull
1
R
SucheNull
0
HolNaechsten1
1
L
HolNaechsten1
1
HolNaechsten1
1
L
HolNaechsten1
=
HolNaechsten1
=
L
HolNaechsten1
0
Zahl2Start
0
R
Mach1Aus0
0
Mach1Aus0
1
L
Mach1Aus0
X
Zahl1Start
X
L
Zahl1Start
1
Zahl1Start
1
L
Zahl1Start
0
SucheStart
0
R
Lösung 6.2
Einfache Verifikation
 Gegeben ist folgender Algorithmus
{a<0, b>0, c>0}
a=b;
{a=b, b>0, c>0}
d=b-a;
{d=b-a, a=b, b>0, c>0}  {d=0, b>0, c>0}
if (c == 0) then
{d=0, b>0, c>0, c=0}
d=5;
{d=5, b>0, falsch}  {d=1}
// aus falsch lässt sich alles folgern
else
{d=0, b>0, c>0, c<>0}  {d+1=1, b>0, c>0}
d=d+1;
{d=1, b>0, c>0}
{d=1, b>0, c>0}  {d=1}
Lösung 6.3
Denksportaufgabe
1. Denksportaufgabe



1. Welche Farbe hat die letzte Kugel ?
Die Farbe der letzten Kugel ist abhängig von der Anzahl der weißen
Kugeln:
Ist die Anzahl gerade, so ist die letzte Kugel schwarz
Ist die Anzahl ungerade, so ist die letzte Kugel weiß
2. Welche Aussage gilt vor, in und nach der Schleife (Invariante)
Ist die Anzahl der weißen Kugeln gerade, so bleibt sie gerade
Ist die Anzahl der weißen Kugel ungerade, so bleibt sie ungerade
Es werden entweder 2 weiße Kugeln entfernt oder keine.
3. Terminiert die Schleife ? Begründen Sie ihre Antwort.
JA. Die Anzahl der Kugeln vermindert sich bei jedem Zug um genau eine
(nach Algorithmus: 2 nehmen, eine geben). Beim Erreichen von 2 Kugeln
wird die Schleife noch einmal durchlaufen und terminiert mit einer Kugel.
Lösung 6.4
{s+w >= 1}
Invariante



x=s; y=w;
{x=s, y=w, x+y  1}
{INV: ( (odd(w)odd(y))  (even(w)even(y)) )  x+y1 }
while (x+y>1)
{
{INV  x+y>1} // Vorbedingung für „take“: x+y>1
take(a,b)
// OUT: a no. black, b no white (drawn)
{a+b=2, a,b0} // = Nachbedingung für „take“
switch a: {
// a = no of black bullets drawn
case 0: {x=x+1; y=y-2}; {INV} // add black, remove two w.
case 1; (x=x-1);
{INV} // remove black
case 2; (x=x-1);
{INV} // remove black
}
{INV}
}
{INV   x+y>1 
( ((odd(w)odd(y))  (even(w)even(y)) )  x+y1  x+y1 
( ((odd(w)odd(y))  (even(w)even(y)) )  x+y=1) }
Lösung 6.5
Vollständige Verifikation
// Vorbedingung P(V): a>0  b0
x = a; y = b; z = 1; // x=a  y=b  z=1  x>0  b0
{ INV: zxy=ab  y0 }
while y > 0 {
{INV  y>0  (z*x/x)*xy=ab  y>0 }
if odd(y) then
z = z*x; { odd(y)  z/x*xy=ab  y>0  z*xy-1=ab  y>0 }
// else
{ even(y) 
z*xy =ab  y>0 } 
{ ( odd(y)  z*x(2(y div 2)+1)-1=ab  2(y div 2)+1>0 ) 
( even(y)  z*x2(y div 2)
=ab  2(y div 2) >0 )
}
y = y div 2; // Ganzzahldivision
{ ( odd(y)  z*x(2y+1)-1=ab  2y+1>0  z*x2y=ab  2y0 ) 
( even(y)  z*x2y
=ab  2y >0  z*x2y=ab  2y>0 )
}
x = x*x;
{ (odd(y)  z*xy=ab  2y0)  (even(y)  z*xy=ab  2y>0) 
z*xy=ab  ((odd(y)2y0)  (even(y)2y0))  z*xy=ab  y0 }
}
{ INV  (y0)  (z*xy=a*b)  (y=0)  z*x0=ab = Q(V) }
Lösung 6.6.1 Schranken
1. g(n) = 5n3 + n + 1000 für alle n
a) Behauptung: Die Laufzeit von g(n) ist O(n3), also f(n)=n3,
b) Beweis:
Es muss Konstanten c und n0 geben, so dass gilt
5n3 + n + 1000  c n2, für alle n > n0
setze z.B. n0=10 und c=6, dann gilt:
n3 > n + 1000 gilt für n11, n  
5n3 + n + 1000  5n3 + 100n  5n3+n3 = 6n3
c) 
14000
n3
12000
10000
8000
6000
4000
2000
d) z.B.: 5n3
0
1
2
3
4
5
6
7
8
9
10
11
12
13
Lösung 6.6.2 Schranken
2. Sie haben zusätzlich einen Algorithmus mit O(2n) Aufwand. Vergleichen
Sie diesen Algorithmus mit dem Algorithmus aus 1.
a) Welches ist der „schnellere“ Algorithmus ?
Für kleine n (n<14) ist der Algorithmus mit O(2n) der schnellere, ansonsten
der mit g(n) = 5n3 + n + 1000
b) Begründen Sie Ihre Antwort quantitativ
35000
2n
30000
25000
20000
15000
10000
5000
0
1
2
3
4
5
6
7
8
9
10
11 12
13
14 15
Lösung 6.7.1 O-Notation
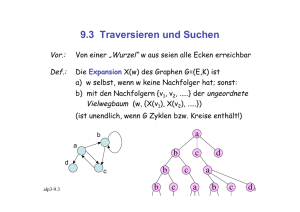
1. gegeben seien folgende Werte: 1,3,4,8,9,15,17,25,28,29,31,36,41,45
17
Anzahl Aufrufe 1
8
3
1
31
9
4
2
28
15
25
41
29
36
3
45
4
node: array[1..14] of knoten;
// Normalerweise wird der Speicher dynamisch allokiert
node[1].value = 17;
node[12].value = 41;
node[1].left = &node[2];
node[12].left = &node[13];
node[1].right = &node[3];
node[12].right = &node[14];
node[2].value = 8;
node[13].value = 36;
node[2].left = &node[4];
node[13].left = nil;
node[2].right = &node[5];
node[13].right = nil;
node[3].value = 31;
node[14].value = 45;
node[3].left = &node[6];
node[14].left = nil;
node[3].right = &node[7];
node[14].right = nil;
...
Lösung 6.7.2 O-Notation
2. Formulieren Sie einen iterativen Algorithmus mit O(n4)
for (i=1 to n) {
for (j=1 to n) {
for (k=1 to n) {
for (l=1 to k) { // Statements
}
}
}
}
Aufwand: nn(n(n+1))/2 = n2(n2/2+n/2)=n4/2 + n3/2
 Laufzeit O(n4)
Lösung 6.8
Aufwand
1. do (list:*liste) {
i:integer;
for i=1 to no_of_elements(list) {
remove_last_element(list);
do (list)
// call list with one element less
}
Zeitbedarf: Tn = n Tn-1 (Tn = Zeitbedarf für n, n2, T1=1)
Tn =nTn-1 = n  (n-1)  Tn-2 = n  (n-1)  (n-2) Tn-3 = ... = 1 2 3 ... n
 Tn = n!  Laufzeit O(n!) (wirklich viel! Algorithmus inpraktikabel)
2. for i=1 to n {
j=1;
while (j<i) { j = j+2; }
}
Zeitbedarf: Betrachte Anzahl der Zuweisungen für alle i<n:
1 + 2 + 2 + 3 + 3 + 4 + 4 + .... + n/2 + n/2 =
2  (n/2  (n/2+1))/2 - 1 = n/2  (n/2 +1) -1 = n2/4 + n/2 - 1
 Laufzeit O(n2)