Elektronik 2 - Formelsammlung

Elektronik 2 - Formelsammlung
1
1.1
Seite 1 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Wandler
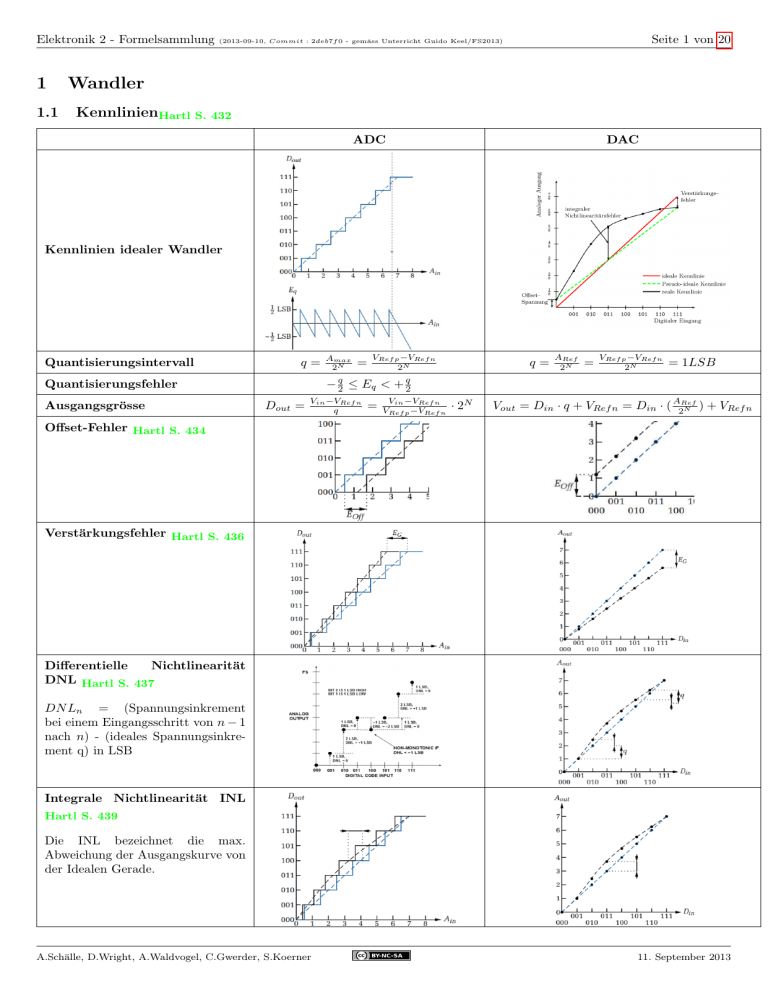
KennlinienHartl S. 432
ADC
DAC
Kennlinien idealer Wandler
Quantisierungsintervall
Quantisierungsfehler
Ausgangsgrösse
V
−V
Amax
= Ref p2N Ref n
2N
− 2q ≤ Eq < + 2q
Vin −VRef n
Vin −VRef n
= VRef
q
p −VRef n
q=
Dout =
q=
· 2N
ARef
2N
=
VRef p −VRef n
2N
= 1LSB
Vout = Din · q + VRef n = Din · (
ARef
2N
) + VRef n
Offset-Fehler Hartl S. 434
Verstärkungsfehler Hartl S. 436
Differentielle
Nichtlinearität
DNL Hartl S. 437
DN Ln = (Spannungsinkrement
bei einem Eingangsschritt von n − 1
nach n) - (ideales Spannungsinkrement q) in LSB
Integrale Nichtlinearität INL
Hartl S. 439
Die INL bezeichnet die max.
Abweichung der Ausgangskurve von
der Idealen Gerade.
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
1.2
Seite 2 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Eigenschaften und Fehler bei dynamischen SignalenHartl S. 442
SFDR (Spurios Free Dynamic Range):
Abstand von der Grundwelle zum höchsten Peak der Harmonischen.
Verzögerungszeit (Settling Time):
Zeit vom Anlegen des Signals bis das Signal innerhalb vom Fehlerband
ist und nicht mehr hinaus geht.
1.2.1
AperturfehlerHartl S. 442
Bei einer periodischen Abtastung eines Signals ist immer ein gewisse zeitliche Unsicherheit im Abtastzeitpunkt (Aperturunsicherheit) gegeben. Ist der Aperturfehler grösser als der maximal auftretende Quantisierungsfehler ( 12 LSB) so verschlechtert
sich die Auflösung des Umsetzers.
1.2.2
Jitterfehler
x(t) = V0 sin(2πf t)
ẋ(t) = 2πf V0 cos(2πt)
EA :
Aperturfehler
max | ẋ(t) |= 2πf V0
Eq :
Quantisierungsfehler
TA :
Zeitfehler
ARef :
analoge Referenz
N:
N bit Auflösung
V0 :
Amplitude
f:
Frequenz
t:
Zeit
x(t):
Signal
EA = 2πf V0 TA
2V0 = ARef
EA < Eq
ARef
q
Eq = =
2
2 · 2N
ARef
EA <
2 · 2N
2V0
2πf V0 TA <
2 · 2N
1
TA <
πf 2N +1
1.2.3
AliasingHartl S. 444
Aliasing entsteht bei Unterabtastung, d.h wenn das Abtasttheorem verletzt wird. Es entstehen falsche, nur scheinbar vorhandene Komponenten im zeitdiskreten Signal.
Abtasttheorem
fS > 2fmax
fs : Abtastfrequenz
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
fmax :max. Frequenz des Signals
11. September 2013
Elektronik 2 - Formelsammlung
2
Seite 3 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
DA WandlerHartl S. 455
Es gibt 3 Verfahren: Parallelverfahren, Wägeverfahren und Zählverfahren.
2.1
Parallelverfahren
Strom-DAC
Hartl S. 456
K = 2N − 1
Iout = D · I = D ·
VRef
R
VRef
(von einer Quelle)
R
K:
Anzahl Stromquellen
D:
Eingangswert (Anzahl Schalter
die aktiv sind.)
Schaltereigenschaften:
On: kein Spannungsabfall
Off: kein Strom
I=
String
DAC
(Voltage
Scaling) Hartl S. 459
Vorteile: garantierte Stetigkeit
Nachteile: benötigt 2n Widerstände und
2n Schalter, n-to-2n Decoder(linke
Variante), er darf nicht belastet werden und hat ein grosser Schaltungsaufwand.
D
(VRef p − VRef n ) + VRef n
2n
VOutreal (D) = VRef n + (VRef p − VRef n ) ·
D · RLoad
· n
2 · R · D − R · D2 + 2n (RLoad + RSwitch )
VOutreal (D) − VOutideal (D)
DACerror (D) =
VOutideal (D)
VOutideal (D) =
Segmented
String
DAC
Hartl S. 459
2.2
Vorteile: viel weniger Elemente
Nachteile: benötigt Buffer (offset-frei)
WägeverfahrenHartl S. 461
Spannungssummierung
Hartl S. 461
B0 · 20 + B1 · 21 + . . . + B(n − 1) · 2n−1
2n
· (VRef p − VRef n ) + VRef n
VOut =
Vorteile: n Widerstände, n Schalter
Nachteile: nicht garantiert stetig, grosse Wertebereiche
für Widerstände, rechnen mit Leitwerten (G0 =
1
8R )
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
Seite 4 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Wägeverfahren
mit
Ausgangstreiber
(Summation
gewichteter Ströme)
Idacmax =
VRef p − VRef n 2n − 1
·
R
2n
Vout und Idac inv sind differentiel zu einander, dadurch
fliesst immer der gleiche Strom und der Offsetfehler
bleibt konstant.
R-2R-Netzwerk
Vout,max = VRef n
Hartl S. 462
Vout,min = VRef n − R · Imax
1
1 1
1 1
+
+
+ . . .)
2R 2 2R 4 2R
1
= (VRef p − VRef n )
(2 − 21−n )
2R
Imax = (VRef p − VRef n )(
Vorteil: nur 2 unterschiedliche R
Nachteil: es muss immer ein Strom fliessen
Vorteil: Man kann bis zur angelegten Referenzspannung durchschalten
Kapazitiver
DAC
(Charge
Scaling)
C1 = B3 · 8C + B2 · 4C + B1 · 2C + B0 · C
C2 =!B3 · 8C+!B2 · 4C+!B1 · 2C+!B0 · C + C
C1
· (VRef p − VRef n ) + VRef n
VOut =
C1 + C2
mit C1 + C2 = 2n · C
Kapazitiver
DAC mit Ausgangstreiber
Wenn z.B. B3 auf VRef 1 geschaltet wird:
QC3 = C3 · ∆U = C3 · (VRef 1 − VRef 2 )
∆Q3 = ∆Qf b = C3 · ∆VRef
∆Qf b
C3
= (VRef 1 − VRef 2 ) ·
⇒ ∆VOut =
Cf b
Cf b
Vout = VRef 2 − ∆VOut
2.3
Zählverfahren(PWM)Hartl S. 466
VOut =
Grundprinzip
Hartl S. 466
D
2n
· (VRef p − VRef n ) + VRef n
Vorteile:
-einfache Schaltung
-ermöglicht hohe Auflösung
-Funktioniert
ohne
Schaltungen on Chip
Nachteile:
analoge
-sehr langsam
-benötigt grosse Zeitkonstanten
N
NT
nT
mod N Counter
PWM-Ansteuerung
Hartl S. 466
N
< n?
Out
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
Vref
0
NT
nT
¯ =
VOut
n
N VRef
N:
Takte
n:
digitale Eingangsgrösse
11. September 2013
Elektronik 2 - Formelsammlung
2.4
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Seite 5 von 20
Weitere DAC
Kaskadierte DAC
• MS-DAC hat 2 Ausgangsspannungen (Über
und unter dem gewünschten VOut )
• LS-DAC hat kleine Eingangspannungsdifferenz
→ höhere Auflösung der Spannung
Zyklisch, algorithmischer DAC Hartl S. 466
Pipelined DAC
Ablauf der Wandlung
1. Die Spannung im S/H löschen (Schalter S1),
S3 offen)
2. S1 auf den Verstärker-Ausgang schalten
3. Laufvariale k wird auf 0 gesetzt
4. S2 setzen: VREF oder GND ( abh. DK ).
5. Der Addierer und Verstärker generieren Ausgangssignal
6. Im S/H wird die Feedback-Spannung gespeichert (S1)
7. X wird um 1 erhöht
8. Gehe zu Schritt 4, wenn X ≤ n
VOut = (D0 · 2−n + D1 · 21−n + ... + Dn−1 · 2−1 ) · VRef
Die Latenz beträgt n Zyklen, die Update-Frequenz
ist aber n-mal grösser, da die Blöcke n-fach vorliegen.
LSB (D0 ): VRef wird n-mal halbiert
Strom-DAC
• Stromspiegel
• MP0 ist gleich breit wie Stromquellen-MOS →
I(MP0) = IRef
MP0: Einheitstransistor
• MP1 ist doppelt so breit wie MP0 → I(MP1) =
2 ∗ IRef
MP1: 2 Einheitstransistoren
• MP2 ist doppelt so breit wie MP1 → I(MP2) =
4 ∗ IRef
MP2: 4 Einheitstransistoren
• ...
2.5
Spezielle Wandler
Digitales Potentiometer Hartl S. 460
Multiplizierende
Wandler
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
• automatisierter Elektronik-Test möglich
• D (digitale Wert) wird im PROM gespeichert
• V(A), V(B) können variabel sein
Wandler bei denen mit Widerständen aus der Referenzspannung Ströme abgeleitet werden. z.B R2RNetzwerk
11. September 2013
Elektronik 2 - Formelsammlung
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Seite 6 von 20
DAC mit Exponentieller Funktion
2.6
Ausgangsverstärker
CF ilter dämpft Glitches beim Umschalten des Digitalwertes.
Vopp = 0V . . . IOU T · (25Ω||1.5kΩ)
1kΩ
1kΩ
Vopn = 0V . . . IOU T · (25Ω||1.5kΩ) ·
= Vopp ·
1.5kΩ
1.5kΩ
1kΩ
Apos = 1 +
500Ω + 25Ω
3
3.1
AD Wandler
Hartl S. 475
Vergleich ADC
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
3.2
Seite 7 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Parallelverfahren und Kaskadenumsetzer
Vorteile:
sehr schnell
keine DAC Rückkopplung
Parallelumsetzer
(Flash-ADC)
Nachteile:
geringe Auflösung
benötigt 2n Widerstände
benötigt 2n − 1 Komperatoren
Kaskadenumsetzer
(Pipeline ADC)
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
Eine
10-bit-Auflösung
beim
Parallelverfahren
würde
1024
Komperatoren
benötigen.⇒Komplexitätsreduktion
Mit erstem N1 -bit ADC wird der Grobbereich
festgelegt (höherwertige Bits). Diese Zahl wird in
eine analoge Spannung durch einen N1 -bit DAC
zurück umgesetzt und diese Spannung von der
Eingangsspannung subtrahiert. Diese Differenz wird
von einem weiteren N2 -bit-ADC umgesetzt, um die
niederwertigen Bits zu ergeben. Skaliert man die
Differenzspannung mit dem Faktor 32, hat man
den gleichen Spannungsbereich, kann also zwei
identische ADC benutzen.
p = Anzahl Stufen
m = Bit pro Stufe
p(2m − 1) Komperatoren
n=p·m
Bild 1:
Pipeline ADC ohne Fehlerkorrektur
Bild 2:
Pipeline ADC mit Fehlerkorrektur
Bild 3:
Verzögerung der Ausgangsdaten gegeüber den Sampels (Latenz)
11. September 2013
Elektronik 2 - Formelsammlung
3.3
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Wägeverfahren (sukzessive Approximation/SAR)
Seite 8 von 20
Hartl S. 485
Prinip SAR
• Abtastung der Eingangsspannung Vin mit einer S&H-Schaltung( Vergleichsspannung liegt
so während der gesamten Umsetzung an)
• Vergleich starte in der Mitte der EingangsspanV
nung Ref
2
Ablauf der Wandlung:
1. Im Sample-Hold wird ein analoger Wert gespeichert
2. X(Laufvariable) wird auf n-1 gesetzt, DACRegister wird auf 0 gsetzt
3. Das Bit Bx vom DAC wird 1 gesetzt
4. Komperator wird ausgewertet
1: Bx = 1, DAC-Bit bleibt gesetzt
0: Bx = 0, DAC-Bit wird gelöscht
5. X wird um 1 reduziert
6. Gehe zu Schritt 3, wenn X ≥ 0
Wägeverfahren
SC-Prinzip
mit
Ablauf der Wandlung:
1. alle C mit Vin laden
2. SC öffnen
3. S2 , . . . , SA an AGN D
4. Sukzessive S2 , . . . , S0 an VRef
Wenn S2 an VRef ist gilt: Vx =−Vin +
VRef
2
Digitaler Wert D = f loor Vqin
nicht aufgelöste Spannung: Vrest = Vin mod q
3.4
Iterative ADC
1.
2.
3.
4.
5.
6.
7.
8.
9.
Im S/H wird die Eingangsspannung geschpeichert (Schalter Sin)
Schalter Sin wird danach auf den Multiplizierer-Ausgang geschaltet
X(Laufvariable) wird auf n-1 gesetzt
Der Komparator wird ausgewertet
Dout=1: Bx=1, Switch S=1 (d.h. im Subtrahierer wird Vrefh von Vc
subtrahiert)
Dout=0: Bx=0, Switch S=0 (d.h. im Subtrahierer wird 0 von Vc subtrahiert)
Der Subtrahierer generiert sein Ausgangssignal
Der Multiplizierer generiert sein Ausgangssignal
Im S/H wird die Feedback-Spannung gespeichert (Schalter Sin)
X wird um 1 reduziert
Gehe zu Schritt 4, wenn X ≥ 0
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
3.5
Zählverfahren
Seite 9 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Hartl S. 490
Ist für kontinuierliche Auswertungen des Eingangssignal
3.5.1
Single Slope
Vin =
3.5.2
VRef · R · C
Tint
Dual Slope Hartl S. 492
Tint = const
Vint (t) = −
Z
1
Rint · Ci
Vint (Tint ) = VAGN D −
t
(Vin (τ ) − VAGN D )dτ + VAGN D
0
1
Rint · Ci
· Tint · (Vin − VAGN D )
Integration:
Vintmax = VAGN D −
(Für Vin = const.)
Abintegration:
Vin − VAGN D
· Tint
Ri · Ci
Abintegrationszeit:
Vint (t) = Vintmax −
VRef − VAGN D
·t
Ri · Ci
Auflösung in Bits:
Tint ·(VAGN D −Vin )
VRef −VAGN D
tabint =
n = log2 (max Taktzyklen von Abintegration)
n
Vin =
· Vref
N
Sinusschwingungen mit einer Periodendauer gleich der Integrationszeit, werden
herausgefiltert!
N:
Taktzyklen
Tint :
Integrationszeit (ist vorgegeben)
T:
Periodendauer
Tabint :
n:
Zählerstand
Vint :
Messzeit”
”
Spannung am VopOut nach der Zeit Tint
Vof f :
Offsetspannung
Vintmax :
maximal mögliche Spannung am VopOut
Offsetkompensation:
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
Möglichkeiten zur Korrektur:
• 2.Referenzspannung VRef p einfügen
• Die Komperator-Schwelle VRef c negativ gegeüber AGN D verschieben
• Dem OP einen Offset in einer Richtung vorgeben, damit er max 0 sein kann.
11. September 2013
Elektronik 2 - Formelsammlung
3.5.3
Seite 10 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Sigma-Delta Wandler Hartl S. 500
Y (s) =
X(s) − Y (s)
1
s
+ Q(s) ⇒ Y (s) = X(s)
+ Q(s)
s
1+s
1+s
Signal UTF:
Hs (s) =
1
1 + sT
SNR-Erhöhung:
Noise UTF:
Hn (s) =
sT
1 + sT
9dB oder 1.5Bit pro Verdoppelung des OSR (OverSamplingRatio)
Hauptnachteil:
Pattern Noise (repetitive Sequenzen, die nicht von Signalen
unterschieden werden können)
Q(s) = Quantisierungsrauschen
3.5.4
Sigma-Delta Wandler 2. Ordnung
3.5.5
PWM vs. Sigma-Delta
Digitalteil PWM
• Zähler zählt bis 2n
• Komperator schaltet Ausgang
• ’1’ sind hintereinander
Digitalteil Sigma-Delta DAC
• Dig.wert wird integriert“
”
• Übertrag schaltet Ausgang
• ’1’ werden verteilt
3.6
3.6.1
Dynamikbereich
Dithering
Ein Signal kann über Mittelwertbildung höher aufgelöst werden, wenn es mit Rauschen überlagert ist. Die Auflösung wird
gegen Bandbreite eingetauscht“ (Die Rauschleistung wird auf die Bandbreite aufgeteilt, dadurch ist nur noch ein kleiner
”
Rauschanteil im Signalband).
3.6.2
Oversampling
Over Sampling Ratio:
OSR =
Signal to Noise Ratio:
SN RdB
fs
2 + fmax
= 1.76dB + n · 6.02dB
SN RdB = 1.76dB + n · 6.02dB + 10 · log(OSR)
(ohne Überabtastung)
(mit Überabtastung)
Durch Überabtastung wird das Quantisierungsrauschen über einen grösseren Frequenzbereich verteilt. Da die Rauschleistungsdichte (= q 2 /12) konstant ist, wird durch eine grössere Bandbreite die Rauschleistungsdichte kleiner.
3.6.3
Effektive Bit-Zahl (ENOB)
Signal to Noise and Distortion:
SIN AD = 10 · log
Effective Number of Bits:
EN OB =
Psignal + Pnoise + Pdistortion
Pnoise + Pdistortion
SIN AD − 1.76
6.02
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
4
Seite 11 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
OpAmps AC
Der Operationsverstärker ist in allgemeiner Näherung ein Tiefpass-Filter n-ter Ordnung mit linearer Verstärkung.
Frequenzgang allgemein
4.1
A(s) =
A0
(1+ ωs )(1+ ωs )...
p1
A0 = Lineare Verstärkung
ωpi = Polkreisfrequenzen
p2
Open-Loop/Closed-Loop Verhalten
Open-Loop
Closed-Loop
Blockschemas
Frequenzgänge
Acl (s) =
(1 +
s
ωpcl
Acl0
)(1 +
1
s
ωpcl
)...
=
Tin (s) · Aol (s)
1 + β(s) · Aol (s)
2
Vopn
Vopp
oder
Vout
Vout
Vopn
Vopp
Tin (s) =
oder
Vin
Vin
β(s) =
Aol (s) =
(1+ ω
s
pol
1
Aol0
)(1+ ω
s
pol
2
)...
Vout = Acl (s) · Vin =
Tin (s) · Aol (s)
· Vin
1 + Aol (s) · β(s)
|
{z
}
Ts (s):Loop−Gain
Durch das Schliessen des Loops wird die Bandbreite vergrössert, das gain-bandwidth-product(GBP) bleibt jedoch konstant. Die Verstärkung wird jedoch um Ts0 (s)
(Linearer Loop Gain) reduziert. Der Phasengang wird
durch das Verschieben des ersten Poles auch verändert,
wie folgende Grafik zeigt.
4.2
Stabilität des Systems
Um die Stabilität des OpAmps zu betrachten, wird der
Loop geöffnet. Damit das System stabil ist, darf das Fehlersignal sich selbst nicht verstärken. Damit dies der Fall
ist muss die Phase > −180◦ sein bei einem Loop Gain
von 1, da das Vergleichsglied die Phase noch um 180◦
dreht.
Ein Mass für die Stabilität ist die Phasenmarge (Phase Margin) und die Verstärkungsmarge (Gain Margin).
Optimal ist ein Phase Margin von 60◦ .
Die UTF ist dann stabil, wenn sie nie ∞ wird d.h der
Nenner darf nie 0 werden.
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
4.3
Seite 12 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
OP als Regelkreis
Nicht-invertierender OP
A = Aol
Tin = 1
R1
1
=
R1 + Rf
T
R1 + Rf
Tin
1
Tin · Aol
Aol
1
≈
=T =
·
=
=
=
1
R
1
β 1 + β·Aol
1 + Aol · β
R1
β
1 + Aol · R1 +Rf
β = Tf =
Vout
Vin
Invertierender OP
A = Aol
Rf
=1−β
Tin =
R1 + Rf
R1
1
β = Tf =
=
R1 + Rf
1−T
1
Rf
Vout
Tin
−Tin · Aol
1−β
·
≈−
=T =−
=
=−
1
Vin
β 1 + β·A
1
+
A
·
β
R
β
ol
1
ol
Closed-Loop-Frequenzgang
Frequenzabhängige Verstärkung Opamp:
A0
A0
Aol (s) =
=
A0
1 + s/ωp
·s
1 + 2π·GBP
eingesetzt in folgende Formel:
Aol
Vout =
· Vin
1 + β · Aol
ergibt:
Acl (s) =
1
A0
1+s/ωp
A0
+ β 1+s/ω
p
A0
=
A0
A0cl
1+A0 β
=
=
1
(1 + A0 β) + s/ωp
1 + s ωp (1+A
1
+
s ωp1
0 β)
cl
Für A0 · β 1 gilt:
• Verstärkung A0cl = 1/β
• Bandbreite wird vergrössert um den Faktor A0 · β

GBW = A0 · ωp 
A0 · ωp  Frequenz bei welcher der Amplitudengang der
GBP =
Verlängerung des 1.Pols die 0dB-Linie schneidet.
2π
Closed-Loop-Bandbreite: Schnittpunkt Acl mit A(ω)
Loop Gain: Aol (s) · β = A(s) · β oder A0dB − A0cldB (nach Grafik)
Unity-Gain: Frequenz wo der Amplitudengang (aller Pole) die 0dB-Linie schneidet.
4.4
•
•
•
•
DC-Betrachtung: (endliche Verstärkung Aol )
Eingangsdifferenzspannung: VAout
ol
1
Verstärkungsfehler: ∼ β·A
ol
Eingangsimpedanz vergrössert um β · Aol
Ausgangsimpedanz dividiert durch β · Aol
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
5
5.1
Seite 13 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
FilterHartl S. 509
Tiefpass-FilterHartl S. 514
1
1+sC·R
1
1+j· ω ω
1. Ordnung
UTF: G(s) :
2. Ordnung
(kaskadierte RCTiefpässe)
1
f3dB = 2πR·C
Bei ω = ω3dB = T1 sind Real- und Imaginärteil gleich gross:
T =R·C
2 2
1
1
G(s) = 1+sRC
= 1+sT
√√
2−1
T = 2π·f
g
Gp (s) =
Uout
Uin
=
=
3dB
1
C1 ·C2 ·R1 ·R2 ·s2 +(C1 ·R1 +C2 ·R1 +C2 ·R2 )·s+1
2.komplexe Pole:
ω2
p1 ·p2
G(s) = (p1 +s)(p
= s2 +s· ω00 +ω2
2 +s)
0
Q
p
p
ω0
ω0
2
p1 = 2Q (1 + 1 − 4Q )
p1 = 2Q
(1 − 1 − 4Q2 )
Vgl. allgemeiner Tiefpass 2. Ordnung:
GLP (s) =
A0
s2
ω02
+
s
Q·ω0
+1
A0 = 1
1
C1 · C2 · R1 · R2
√
C1 · C2 · R1 · R2
Q=
R1 · (C1 + C2 ) + C2 · R2
ω0 = √
Schrittantwort:
identische Pole:
t
yσ (t) = 1 − e − T · (1 +
t
)
T
ungleiche Pole:
t
yσ (t) = 1 −
t
T1 · e − T1 − T2 · e − T2
T 1 − T2
!
komplexe Pole:
ω0
yσ (t) =1 − e − 2Q ·t ·
"
#
ω0 p 2
1
ω0 p 2
cos
4Q − 1 · t + p
· sin
4Q − 1 · t
2Q
2Q
4Q2 − 1
Passive RC-Filter können maximal Güte von 0.5 haben (2 identische reelle Pole) Filter höherer Güte werden Spulen oder
Verstärker benötigt. Für Systeme 2.Ordnung ist eine Polgüte von
0.7 optimal.
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
Seite 14 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Sallen Key
(Einfachmitkopplung)
Hartl S. 517
Standard Sallen Key
Stromgleichungen:
0 = (U2 − Uin ) · R11 + (U2 − U3 ) ·
0 = (U3 − U2 ) · R12 + U3 · sC2
Verstärkung:
B
Uout = G0 · U3 mit G0 = RAR+R
B
1
R2
+ (U2 − Uout ) · sC1
G0
C1 · C2 · R1 · R2 · s2 + [C2 · (R1 + R2 ) + C1 · R1 · (1 − G0 )] · s + 1
1
ω0 = √
C1 · C2 · R1 · R2
√
C1 · C2 · R1 · R2
QSK =
C2 · (R1 + R2 ) + C1 · R1 · (1 − G0 )
Die Güte kann mit G0 beeinflusst werden. SK-Filter sind für grosse
Güten nicht geeignet.
GSK =
Multiple
back
Feed-
Hartl S. 522
für hohe Frequenzen
• Wenn der Opamp nicht mehr verstärkt
• C1 , C2 wirken als Kurzschlüsse
VOut
rOL k R2 k (RA + RB )
rOL
=
≈
Vin
R1 + rOL k R2 k (RA + RB )
R1 + rOL
• Folge: Sallen Key-Filter sind nicht geeignet für Systeme mit
hohen Frequenzanteilen, z.B. PWM-DAC
• rOL : OpAmp OpenLoop Ausgangswiderstand
Stromgleichungen: (Opamp sorgt für U3 = 0)
0 = (U2 − Uin ) · R11 + (U2 − Uout ) · R12 + (U2 − U3 ) · R13 + U2 · sC1
0 = (U3 − U2 ) · R13 + (U3 − Uout ) · sC2
G0
mit
R
1+C2 (R2 +R3 +R3 · R2 )·s+C1 ·C2 ·R2 ·R3 ·s2
1
√
C1 ·C2 ·R2 ·R3
ω0 = √C ·C1·R ·R
R
1
2
2
3
C2 ·(R2 +R3 +R3 · R2 )
Gmf (s) =
Qmf =
2
G0 = − R
R1
1
Die Güte wird v.a. eingestellt mit C2 und R1 , grosse Güte für kleines C2 und grosses R1 . C2 beeinflusst auch das Frequenzverhalten,
R1 die Verstärkung.
Zustandsvariablen-Filter
Spannungsgleichungen:
1
· Vopo2
sCi2 · Ri2
R2
=−
· Vopo1
R1
−1
Vin
Vout
=
·
+
+ sCf b · Vout
sCi1
Rin
Rf b
V out = −
Vopo2
Vopo1
R
Gss (s) =
− Rfinb
Ci1 · Ci2 · Ri2 · Rf b ·
A0 = −
· s2 + Cf b · Rf b · s + 1
Rf b
Rin
ω0 = q
q
Q=
R1
R2
1
Ci1 · Ci2 · Ri2 · Rf b ·
Ci1 · Ci2 · Ri2 ·
R1
R2
R1
Rf b ·R2
Cf b
D.h. mit dieser Topologie sind alle 3 Parameter frei wählbar!
1. ω0 mit Ci1 , Ci2 , Rf b , Ri2 , R1 , R2
2. Q mit Cf b
3. A0 mit Rin
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
6
Seite 15 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
PCBs, Printed Circuit Boards
Kapazität
einer Leiterbahn
Plattenkapazität:
w·l
C p = εr · ε0 ·
d
Side-wall-Kapazität:
ε0 = 8.85pF/m
h
Csw = εr · ε0 · 2l · ln 1 +
d
Gesamtkapazität einer Leiterbahn:
h
w·l
C = Cp + Csw = εr · ε0 · 2l · ln 1 +
+
d
d
Leiterbahn
Dielektrikum
Induktivität
einer Leiterbahn
7
l: Länge
d: Dicke
2l
+ 0.2235 ·
L = l · ln w+h
w: Breite
w+h
l
h: Höhe
+ 0.5 · 200 nH
m
Passive Elemente
l
w·d
Widerstand
R=ρ·
PTC (Kaltleiter)
am Beispiel
PT1000
Berechnung des Widerstandes für Temp > 0°C:
R = R0 · (1 + αt + βt2 )
Berechnung des Widerstandes für Temp < 0°C:
ρ: Spezifischer Widerstand
R = R0 · [1 + αt + βt2 + γ · (t − 100◦ C) · t3 ]
α = 3.9083 · 10−3 1/◦ C
β = −5.775 · 10−7 1/◦ C 2
γ = −4.183 · 10−12 1/◦ C 4
NTC
(Heissleiter)
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
B· T1 − T1
R
RT = RR · e
RT : NTC-Widerstand bei Temperatur T in Kelvin
RR : NTC-Widerstand bei definierter Temperatur TR in Kelvin
11. September 2013
Elektronik 2 - Formelsammlung
Seite 16 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
C = εr · ε0 ·
Kondensator
W ·L
d
= εr · ε0 ·
A
d
ε0 = 8.85pF/m
Ladevorgang:
t
t
uC (t) = U0 · 1 − e− τ = U0 · 1 − e− R·C
t
U0 − t
· e τ = I0 · e− R·C
R
Entladevorgang:
iC (t) =
t
t
uC (t) = U0 · e− τ = U0 · e− R·C
t
U0 − t
· e τ = −I0 · e− R·C
iC (t) = −
R
Dielektrizitätsklassen:
Code
C0G, NP0
Induktivität
◦
X5R, X7R
Y5U, Z5U
Temperaturbereich
−55 . . . 125 C
X5R:
−55 . . . 85◦ C
X7R:
−55 . . . 125◦ C
Y5U:
−30 . . . 85◦ C
Z5U:
10 . . . 85◦ C
Kapazitätsänderung
über Temperaturbereich
0 ± 30ppm
±15%
±40%
max. Kapazität
im
1206
Gehäuse
0.1µF/25V
X5R:
100µF/6.3V
X7R:
10µF/16V
22µF/16V
µ0 µr A
Ringspule
2πr
µ0 µr A
L = N2 ·
Zylinderspule
l
N ·Φ
dΦ
L=
ui = −N ·
I
dt
Ladevorgang:
U t
R
0
· 1 − e−t· L
iL (t) = I0 · 1 − e− τ =
R
− τt
−t· R
L
uL (t) = û · e
= û · e
L = N2 ·
Entladevorgang:
t
U0 −t· R
·e L
R
R
= −û · e−t· L
iL (t) = I0 · e− τ =
t
uL (t) = −û · e− τ
Cp
RLeak
ESR
ESL
C
Ersatzschaltung Kondensator
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
L
RCu
Ersatzschaltung Spule
11. September 2013
Elektronik 2 - Formelsammlung
8
Seite 17 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Rauschen
Typen von Rauschen
Shot / Schottky
quantum noise
/
Thermisches Rauschen
/Johnson Noise / weisses Rauschen
Flicker Noise / 1/f noise / rosa Rauschen /
Funkelrauschen
• Verursacht durch zufällige Fluktuationen der Bewegung von Ladungsträgern, die Potentialbarrieren
überwinden müssen
• Charakteristik
– geknüpft an Stromfluss
– Unabhängig von Temperatur
– Spektral flach“
”
• Zufällige Bewegung der Ladungsträger aufgrund der Wärmeenergie
und der Quantisierung der Ladung
• Konstant für alle Frequenzen
• alle Widerstände haben ein weisses
Rauschen
• Entsteht in MOS-Transistoren
• Rauschleistung nimmt umgekehrt
proportional zur Frequenz ab.
q
2B
Esh = kT qI
dc
Esh = 0.4µV @1mA, 1M Hz
k: Bolzmannkonstante (1.38 · 10−23 Joule/◦ K)
q: Elektronenladung (1.6 · 10−19 Coulomb)
T: Temperatur in ◦ K
Idc : Durchschnittlicher DC Strom in A
B: Bandbreite in Hz
s
En = Kv
ln
fmax
fmin
s
fmax
fmin
E: Spannungsdichte
In = Ki
Burst (popcorn) noise
Avanlanche noise
ln
I: Stromdichte
• ensteht bei Kristallgitter-Fehlern
• diskrete HF-Pulse
• entsteht in Dioden, im Reverse
”
breakdown“ mode (z.B Zenerdioden)
• Lawineneffekt
Rausch-Farben
Color
Frequency Spectrum
Color
Frequency Spectrum
Purple
f2
Blue
f
White
1
Pink
1
f
Red/Brown
1
f2
Leistung des Rauschens
Mittelwert
Varianz (Leistung)
Effektivwert
R
vn (t) ≤ vn (t) ≥ T1 T vn (t)dt = 0
R
vn (t)2 = T1 T vn2 (t)dt 6= 0
q
vn,rms = vn (t)2
Vnpp w 6 · VnoiseT RM S
Rechnen mit Rauschen: Signale und Rauschen addieren sich nicht gleich:
• deterministische Signale: Amplituden addieren sich
• statistisch unabhängige Rauschquellen: Rauschleistung addiert sich
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
Seite 18 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Rauschen von Widerständen
Strom- und Spannungsrauschen
[V2 /Hz]
√
[V/ Hz]
Z EN B
2
vn = 4kT RB =
4kT R df
Snoise (R) = 4kT R
√
Enoise (R) = 4kT R
0
Z
EN B
i2n = 4kT GB =
4kT G df
0
q
√
vrms = vn2 = 4kT RB
B: Bandbreite
T: Temperatur in Kelvin (typ: 293K =20
ˆ ◦ C)
−23
−1
k: 1.38 · 10 JK
Snoise (R): Spektrale Dichte (Leistungsdichte)
Enoise (R): Rauschspannungsdichte
vRM S : Rauschspannung
EN B: Effective Noise Bandwidth
Widerstände in Serie
2 + v2
vn2 = 4kT (R1 + R2)B = vn1
n2
R1
R2
i2n = 4kT (G1 + G2)B = i2n1 + i2n2
Spannungsteiler
Superposition der einzelnen Spannungsquellen
R2
Vout (Vin ) = Vin ·
R1 + R2
R2
Vout (VnR1 ) = VnR1 ·
R1 + R2
R1
Vout (VnR2 ) = VnR2 ·
R1 + R2
"
Vn2out
= SR1
2
+ SR2
2 #
B
R1
4kT R1 B
r
=
Quellenumwandlung machen und
dann Rauschen über Ersatzwiderstand (RT ) bestimmen.
R1
R1 + R2
R12
R22
+
R
B
2
(R1 + R2 )2
(R1 + R2 )2
R1 · R2
·B
= 4kT ·
R1 + R2
v
u
2
2
u
R2
R1
2
2
=u
V
+
V
t nR1 R + R
nR2
R1 + R2
1
2
↑
↑
= 4kT
Vnout
R2
R1 + R2
VT,s = Vs
4kT ·
4kT R2 B
R1 · R2
·B
R1 + R2
R3
R1 + R3
vT2 n = 4kT RT B
= 4kT (R2 + R1 k R3 )B
Rauschen von RC-Netzwerken
G
Z
C
G − jωC
1
= 2
H(jω) = Z =
G + jωC
G + ω2 C 2
q
q
vn = vn2 = i2n · |Z|2
s
Z
4kT G ∞
1
=
dω
2 + ω2 C 2
2π
G
0
r
kT
=
C
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
• Kapazitäten (und Induktivitäten) rauschen
nicht!
• Kapazitäten (und Induktivitäten) ändern
die Bandbreite des Systems, d.h. beeinflussen dadurch die Rauschspannung
• Der Widerstand trägt nicht direkt zur
Rauschspannung bei, er limitiert die Bandbreite
11. September 2013
Elektronik 2 - Formelsammlung
Seite 19 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Berechnung der Rausch-Spannung
Die Rausch-Spannung ist
das Integral der Rauschspannungsdichte über den
ganzen Frequenzbereich
für weisses Rauschen
Z fH
2
C df = |{z}
C (fH − fL )
Vn =
C: Rauschleistungsdichte pro Hertz (konstant)
für 1/f-Rauschen
Z fH 2
K
fH
2
df = K 2 ln
Vn =
f
fL
fL
K: Bauteil-Konstante (in Volt)
fL
4kT ·R
Berechnung der Rausch-Spannung (am Beispiel von Tiefpass 1. Ordnung)
sZ
∞
eon : Rauschspannung am Ausgang
An(f ) 2 e2 df
eon =
in
der Schaltung
0
2
1
1
⇒ An(f ) =
1 + j2πf RC
1 + (2πf RC)2
sZ
v
u
∞
1
u 1 π
df
=
e
= ein
u
in
2
t|2πRC
1 + (2πf RC)
0
{z 2}
An(f ) =
eon
EN B
r
= ein
1
4RC
Filter-Ordnung
1
2
3
4
ENB
1.57 · fc
1.11 · fc
1.05 · fc
1.025 · fc
ein : Rauschspannung am Eingang der Schaltung
fc : 3dB-Frequenz
ENB: Effective Noise Bandwidth
Es wird nicht die 3dB-Bandbreite,
sondern das gesamte integrierte
Rauschen berechnet
Rauschen in Opamps
Vorgehen zur Bestimmung der Rauschspannung:
1. Verstärkungen bestimmen:
Vout = AOP · Vin + Aref · Vref + Agnd · Vgnd
2. GBW bestimmen
3. Effektive Rausch-Bandbreite bestimmen:
GBW π
EN B =
·
AOP 2
4. Eingangsrauschspannungsdichte bestimmen
5. auf den Ausgang projizieren: Eout = Ein · A
q
6. Eouttot = E12 + E22 + . . .
√
7. Ausgangsrauschspannung: Vnout = Eouttot · EN B
Grundsätzlich gilt, jede Rauschspannungsquelle einzeln betrachten und auf den Ausgang
projizieren.
√
E: Rauschspannungsdichte [V / Hz]
Vn : Rauschspannung [V ]
Beispiel zum untersten Bild:
Rf + R1
Rf
Rf
Vout =
·Vin −
·Vref −
·Vgnd
mit R1 = R11 ||R12
R1
R11
R12
| {z }
|{z}
|{z}
AOP
Aref
Agnd
p
√
ER11 out = Aref · 4k · T · R11
ERf out = 4k · T · Rf
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
11. September 2013
Elektronik 2 - Formelsammlung
Signal-Rauschabstand (SNR)
2 n−1 2
2
·q
Amax
√
= 22n−3 · q 2
=
Psig =
c
2
PQ ≈
q=
q2
12
9.1
c:
q:
Psig :
PQ :
SNR:
√
Crestfaktor (Sinussignal c = 2)
Quantisierungsintervall
Signalleistung
Quantisierungsrauschleistung
Signal to Noise Abstand
VRef p − VRef n
2n
SN Rdb = 10 · log
9
Seite 20 von 20
(2013-09-10, Commit : 2deb7f 0 - gemäss Unterricht Guido Keel/FS2013)
Psig
PQ
= 1.76 + n · 6.02
ReferenzspannungenHartl S. 276
Temperaturdrift von Referenzspannungen
Wenn die Referenzspannung über den ganzen Temperaturbereich nicht mehr als 1 LSB driften darf:
Auflösung (bit)
Anzahl Schritte
1 LSB bei VRef = 2.5V
Max. Temperatur Drift
(ppm/°C) 0. . . 70 °C
Max. Temperatur Drift
(ppm/°C) -40 . . . 85 °C
8
256
9.766 mV
111.61
62.50
10
1024
2.441 mV
27.90
15.63
12
4096
610 µV
6.98
3.91
14
16384
153 µV
1.74
0.98
16
65536
38 µV
0.44
0.24
20
1048576
2.38 µV
0.03
0.015
9.2
Varianten von Referenzspannungen bei 9.3
Wandlern
A.Schälle, D.Wright, A.Waldvogel, C.Gwerder, S.Koerner
Typ. Temperaturdrifts
11. September 2013