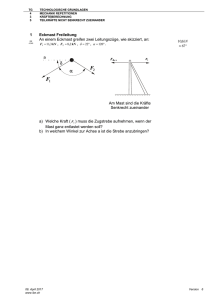
Mechanik
Werbung

TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 4 Mechanik Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055 - 654 12 87 Ausgabe: November 2011 Ausgabe: 11. Dezember 2013 www.ibn.ch Auflage 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK Inhaltsverzeichnis BiVo 4 MECHANIK 4.1 Grundlagen 4.1.1 Vorwort 4.1.2 Basisgrössen 4.1.3 Zusammenhang elektrischer, mechanischer und Wärmearbeit 4.1.4 Masse, Volumen und Dichte 4.1.5 Massvorsätze 4.2 Gleichförmige geradlinige Bewegung Kreisförmige Bewegung Beschleunigung Horizontaler und schiefer Wurf Der freie Fall Kräfteberechnung 4.3.1 4.3.2 4.3.3 4.3.4 4.3.5 4.3.6 4.3.7 4.3.8 Kräftedarstellung Gewichtskraft Kräfteaddition Teilkräfte senkrecht zueinander Teilkräfte nicht senkrecht zueinander Federkraft Beschleunigungskraft Spezielle Kräfte 4.4 Drehmoment und Seilrollen 4.5 Die Reibung 4.4.1 4.4.2 4.4.3 4.4.4 4.5.1 4.5.2 4.5.3 4.5.4 4.6 Drehmoment Seilrollen Drehmoment auf gleicher Welle Drehmoment auf ungleicher Welle Haftreibung Gleitreibung Haftzahl, Gleitreibungszahl und Rollreibungszahl Reibung auf schiefer Ebene Druck 4.6.1 4.6.2 4.6.3 4.6.4 Auflagedruck Hydraulischer oder Stempelddruck Auftriebskraft Hydrostatischer Druck oder Gewichtsdruck 4.7 Mechanische Arbeit 4.8 Die mechanische Leistung 4.7.1 4.7.2 4.7.3 4.8.1 4.8.2 4.8.3 4.9 TD Horizontale Bewegung Vertikale Bewegung Kinetische Energie Mechanische Leistung Horizontalbewegung Mechanische Leistung Wasserturbine Mechanische Leistung aus Drehmoment und Drehzahl Wirkungsgrad 11. Dezember 2013 www.ibn.ch Technische Dokumentation BET Bearbeitungstechnik 2.1 Werkstoffe 2.1.2 Mechanische Eigenschaften - Verhalten bei Krafteinwirkung: Festigkeiten, Härte, Sprödigkeit, Elastizität, Plastizität - Dichte - Eignung für technologische Verfahren: (Formen, Fügen, Vergüten, Veredeln) Bewegungslehre 4.2.1 4.2.2 4.2.3 4.2.4 4.2.5 4.3 Probleme umfassend bearbeiten Verstehen und anwenden Erinnern 2.3 Einsatz der Werkzeuge und Arbeitsgeräte 2.3.5 Berechnungsaufgaben - Drehzahl - Umfangsgeschwindigkeiten - Drehmoment TG 3.5 Technologische Grundlagen Erweiterte Fachtechnik 3.5.1 Internationales Einheitensystem - Internationales Einheitensystem (SI) - Übersicht über die Basisgrössen und Einheiten - Abgeleitete Einheiten von Grössen der Fachgebiete (Beispiele) - Definitionen elektrischer Grössen und Einheiten - Massvorsätze von Einheiten 3.5.2 Nichtelektrische Systeme - Übersicht über technische Energiewandlungssysteme (Teilsysteme) - Erzeugungsarten: Erneuerbare und nichterneuerbare Energie - Zusammenwirken mit dem elektrotechnischen System, Energiefluss, Energieäquivalenz, Bedeutung der Energieformen 3.5.2 Berechnungsaufgaben - Energie, Leistung, Wirkungsgrad bei mechanischen, chemischen, thermischen und strahlenden Vorgängen 3.5.3 Mechanische Vorgänge - Erzeugung und Nutzung mechanischer Kräfte und Körperbewegungen; Erdfeld - Energieübertragung durch mechanische Kraftleitung (Kraftübertragung), Körperbewegung (Erklärungen z.B. anhand vergleichbarer Darstellung: elektrotechnisch - mechanisch-technisches System 3.5.3 Mechanische Grössen (Berechnungsaufgaben) - Geschwindigkeit gleichförmiger, geradliniger und kreisender Bewegungen - Beschleunigung, Erdbeschleunigung - Kraft (Wechselwirkung), Reibungskraft und Drehmoment - Druck bei festen, flüssigen und gasförmigen Stoffen EST Elektrische Systemtechnik KOM Kommunikationstechnik Version 6 TG 4 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK Seite 3 Mechanik Wissen das nicht jeden Tag zunimmt, wird täglich abnehmen. Chinesisches Sprichwort 4.1 Grundlagen 4.1.1 Vorwort Die allgemeine Aufgabe der Physik besteht darin, Erkenntnisse über Naturvorgänge festhalten, zu erweitern, in Gesetze zu fassen und damit Grundlagen für die technische Anwendung zu schaffen. Den theoretischen Teil, „die Geistesarbeit“, nennt man: Physikalische Forschung Der immerwährende Versuch, die neuen Erkenntnisse der Physik im täglichen Leben auszunutzen, nennt man: Technische Entwicklung Die Physik kann in folgende Gebiete unterteilt werden: Gebiet der physikalischen Forschung Gebiet der technischen Anwendung Mechanik Strassen, Brücken, Schiffe, Maschienen, Fahrzeuge, Apparate, Gebäude Nachrichtentechnik Telefonie Telekommunikation Industrie, Gewerbe, Landwirtschaft Maschienen Apparate Medizin Computer Heizungstechnik Klimatechnik Wärmeapparatebau Energieerzeugung Schiffsbau Waffen Akustik Physik Elektrizitätslehre Wärmelehre Kernphysik 11. Dezember 2013 www.ibn.ch Statik Kinetik Kinematik Version 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK VORWORT Seite 4 Die Mechanik und Elektrizitätslehre bildet einen Teil im Grossen naturwissenschaftlichen Gebiet der Physik. Es ist von grösster Bedeutung, dass jeder Lernende die Lehre der Mechanik und Elektrizität in theoretischer und anwendungstechnischer Hinsicht möglichst zu verstehen versucht und weitere Kenntnisse sammelt in den übrigen Teilgebieten der Physik. Der Realist spürt: Sage es mir - ich vergesse es, Zeige es mir - ich erinnere mich, Lass es mich tun - ich verstehe es. (Chinesisches Sprichwort) Wichtige Erkenntnisse: Die Neugier steht immer an erster Stelle eines Problems, das gelöst werden will. (Galileo Galilei) Ich fühle mich nicht zu dem Glauben verpflichtet, dass derselbe Gott, der uns mit Sinnen, Vernunft und Verstand ausgestattet hat, von uns verlangt, denselben nicht zu benutzen. (Galileo Galilei) Wer die Geometrie begreift, vermag in dieser Welt alles zu verstehen. (Galileo Galilei) Die Naturwissenschaft ohne Religion ist lahm, die Religion ohne Naturwissenschaft ist blind. (Albert Einstein) 11. Dezember 2013 www.ibn.ch Version 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK 4.1.2 Seite 5 Basisgrössen 4.1.2.1 Definitionen der Basisgrössen Zum messen physikalischer Grössen legt man Einheiten zu grunde. Die physikalischen Gesetze ermöglichen es, die Zahl dieser Einheiten, mit Hilfe der Beziehungen zwischen den Grössen, in engem Rahmen zu halten. Deshalb befassen wir uns vorerst mit den sogenannten Basis- bzw. Grundgrössen SI-Einheiten (Das internationale Einheitensystem) Im SI-Einheitensystem werden mit sieben Basisgrössen alle Gebiete der Physik abgedeckt. Definition Basisgrösse Länge Formelzeichen l Einheit [m]]=Meter Definition Basisgrösse Masse Formelzeichen m Einheit [kg]]= Kilogramm 11. Dezember 2013 www.ibn.ch Version 6 TG 4 1 1 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN BASISGRÖSSEN DEFINITION DER BASISGRÖSSEN Seite 6 Definition Basisgrösse Zeit Formelzeichen t Einheit [s]=Sekunden Definition Basisgrösse Strom Formelzeichen I Einheit [A]=Ampére Definition Basisgrösse Temperatur Formelzeichen T Einheit [K]=Kelvin 11. Dezember 2013 www.ibn.ch Version 6 TG 4 1 1 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN BASISGRÖSSEN DEFINITION DER BASISGRÖSSEN Seite 7 Definition Basisgrösse Stoffmenge Formelzeichen ρ Einheit [mol]=Molare Masse Definition Basisgrösse Lichtdstärke Formelzeichen I Einheit [cd]=Candela 11. Dezember 2013 www.ibn.ch Version 6 TG 4 1 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN BASISGRÖSSEN Seite 8 4.1.2.2 Abgeänderte Basis-Einheiten Ausser den unter den Basisgrössen aufgeführten Einheiten sind auch weitere verkleinerte oder vergrösserte - Einheiten gesetzlich erlaubt. Längen [m]] µm, mm, cm, dm, km Zeit [s]] ms, min., Std=h, Tg=d, Jahr=a Strom [A]] µA, mA, kA Gewicht [kg]] g, mg, t Volumen [m3] [dm3], [cm3], [mm3] 11. Dezember 2013 www.ibn.ch Version 6 TG 4 1 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN BASISGRÖSSEN 4.1.2.3 Seite 9 Übungen zu SI-Einheiten Alle weiteren Einheiten werden mittels physikalischen Gesetzen aus den äusserst präzis definierten SIBasis-Einheiten abgeleitet. Beispiele: Für die Fläche gilt Für die Geschwindigkeit gilt Für die Arbeit gilt Die Gewichtskraft Beschleunigung 11. Dezember 2013 www.ibn.ch Version 6 TG 4 1 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN BASISGRÖSSEN 4.1.2.4 Seite 10 Übersicht über die wichtigsten SI Einheiten der Physik In der nachfolgenden Übersicht sind die lichttechnischen und elektromagnetischen Einheiten nicht berücksichtigt. 11. Dezember 2013 www.ibn.ch Version 6 TG 4 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN 4.1.3 Seite 11 Zusammenhang elektrischer, mechanischer und Wärmearbeit Mechanische Arbeit Mechanische Arbeit Wärme Energie Elektrische Arbeit W = F ⋅s Horizontale zeitabhängige Bewegung Bewebungskraft in [N]] FR m 1 Nm 1J 1 Ws F Zeit t in Sekunden Weg s in Meter W Mechanische Arbeit [Nm] F s Kraft [N ] Weg [m] W Elektrische Energie Elektrische Arbeit [Ws] P t Elektrische Leistung [W ] Zeit [s ] Q m c Wärmeenergie [J ] [kg ] FG = FN 1 Bei den Übergängen zu den anderen Energieformen treten meistens Verluste auf, welche bei der Umrechnung mit Wirkungsgraden berücksichtigt werden müssen. 2 Elektrische Arbeit W = P ⋅t Umrechnung Energie bzw. Arbeit I kWh UV U kWh-Zähler Wärme Energie Mechanische Arbeit Wärme Energie [Nm] [J ] Elektrische Arbeit [Ws ] [Wh ] [kWh ] 1 1 1 3600 3600 3600 1 3´600´000 3´600´00 0 3´600´000 1´000 1 Q = m ⋅ c ⋅ ∆ϑ Thermometer R Heizung W ärmeinhalt im W asser 11. Dezember 2013 www.ibn.ch Wichtige Einheiten bzw. Vorsatzzeichen für die Darstellung der Energie sind: Kilo k 10 3 Mega M 10 6 Giga G 9 10 Masse Wärmekapazität kJ kg °C ∆ϑ Temperaturdifferenz [°C ] Version 6 TG 4 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN 4.1.4 Seite 12 Masse, Volumen und Dichte Die Masse ist eine Grundgröße der Physik. Ihre SI-Einheit ist das Kilogramm. Sie ist zum einen Ursache der Gravitation („schwere Masse“), zum anderen ein Maß für die Trägheit eines Körpers, das heißt seinen Widerstand gegenüber Änderun-gen seines Bewegungszustands („träge Masse“). m =V ⋅ρ In Sèvres (Vorort von Paris) wird das Urkilo und der Urmeter aufbewahrt. Masse m V ρ Masse [kg ] Volumen [dm 3 ] Dichte [kg / dm 3 ] Die verschiedenen Körperformen für die Bestimmung der Volumen finden Sie unter dem Kapitel der Mathematik: Volumen Dichte 11. Dezember 2013 www.ibn.ch Version 6 TG 4 1 Seite 13 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN 4.1.5 Massvorsätze 4.1.5.1 Vorsatzzeichen Zur Vereinfachung der Schreibweise werden folgende Vielfache und Bruchteile von Dekaden verwendet. Vorsatz Tera Giga Mega Kilo Hekto Deka 11. Dezember 2013 www.ibn.ch Vorsatzzeichen Zehnerpotenz Vorsatz Vorsatzzeichen Zehnerpotenz Dezi Zenti Milli Mikro Nano Piko Femto Version 6 TG 4 1 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK GRUNDLAGEN MASSVORSÄTZE Seite 14 4.1.5.2 Griechisches Alphabet Das griechische Alphabet umfasst 24 Buchstaben. Grossbuchstaben 1. Α 2. Β 3. Γ 4. ∆ 5. Ε 6. Ζ 7. Η 8. Θ 9. Ι 10. Κ 11. Λ 12. Μ 13. Ν 14. Ξ 15. Ο 16. Π 17. Ρ 18. Σ 19. Τ 20. Υ 21. φ 22. Χ 23. Ψ 24. Ω 11. Dezember 2013 www.ibn.ch Kleinbuchstaben α β γ δ ε ζ η ϑ ι κ λ µ ν ξ ο π ρ σ τ υ ϕ χ ψ ω Transliteration a b g d e z ë (gespr. Ä) th i k l m n x o p r s t y (gespr. ü) ph (gespr. f) ch ps õ Name Alpha Beta Gamma Delta Epsilon Zeta Eta Theta Iota Kappa Lambda My Ny Xi Omikron Pi Rho Sigma Tau Ypsilon Phi Chi Psi Omega Version 6 TG 4 2 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE GLEICHFÖRMIGE GERADLINIGE BEWEGUNG 4.2 Seite 15 Bewegungslehre 4.2.1 Gleichförmige geradlinige Bewegung 4.2.1.1 Theorie Gleichförmige geradlinige Bewegung Auftrag Stellen Sie in die zwei nachfolgenden Grafiken den Bewegungsverlauf grafisch dar und die halten Sie die wichtigsten Erkenntnisse in Stichworten und die formalistischen Beziehungen fest. Wichtige Erkenntnisse 0 1 2 Geschwindigkeit-Zeit-Diagramm Formalistische Beziehungen 0 11. Dezember 2013 www.ibn.ch Weg-Zeit-Diagramm Version 6 TG 4 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE Seite 16 4.2.2 Kreisförmige Bewegung 4.2.2.1 Berechnungen der Kreisbewegung Wenn ein Rad auf dem Boden abrollt, so legt ein Punkt auf dem Radumfang den gleichen Weg zurück wie das Fahrzeug bei seiner Vorwärtsbewegung. Somit ist die Umfangsgeschwindigkeit v des Rades gleich gross wie die Geschwindigkeit v des Fahrzeuges. Die Kreisbewegung eines Massepunktes heißt gleichförmig, wenn der Betrag (v) seiner Bahngeschwindigkeit konstant ist. Die Zeit, die der Massepunkt für einen Umlauf auf der Kreisbahn braucht, wird Umlaufdauer (T) genannt. Hat der Kreis den Radius r, gilt für die Geschwindigkeit der Kreisbewegung Periodendauer T v= [ s] 2 ⋅π ⋅ r = 2 ⋅π ⋅ f ⋅ r T Die Winkelgeschwindigkeit ω Winkelgeschwindigkeit Die Winkelgeschwindigkeit gibt an, welchen Winkel (im Bogenmaß) der Fahrstrahl in einer Sekunde zurücklegt. Der Punkt P legt bei jeder Umdrehung den Kreisumfang U = d ⋅ π zurück. Bei N Umdrehungen ergibt sich eine Strecke von d ⋅ π ⋅ N . Der zurückgelegte Weg dividiert durch die dafür benötigte Zeit nennt man Umfangsgeschwindigkeit. v Umfangsgeschwindigkeit d Kreisdurchmesser N Anzahl Umdrehungen t Zeit f Frequenz [ Hz ] = [ s −1 ] n Drehzahl [ s −1 ] , [min −1 ] Der Ausdruck 2 ⋅ π ⋅ f = 2 ⋅ π / T fasst man oft zu einer neuen Größe ϖ = 2 ⋅π ⋅ f v= zusammen. d ⋅π ⋅ N = d ⋅π ⋅ n t f = 1 T f = N =n t [m / s] [ m] [−] [ s] Kreisförmige Bewegungen kommen in unserem Umfeld überall vor. Auf Jahrmärkten und in Vergnügungsparks ebenso wie beim Sport (Diskusoder Hammerwurf) und im Verkehr (Radfahren, Autofahren). Bei der Arbeit (Bohren, Schleifen und Fräsen). Viele technische Anwendungen basieren auf Kreisbewegungen (Motoren, Getriebe, GPSSatelliten auf der Erdumlaufbahn. 11. Dezember 2013 www.ibn.ch Version 6 TG 4 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE Seite 17 4.2.2.2 Kreisbewegung der Netzspannung Kreisfrequenzdarstellung anhand der Netzfrequenz von f=50 Hz! t [ms] α [°] Berechnungen 11. Dezember 2013 www.ibn.ch Version 6 TG 4 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE Seite 18 4.2.3 Beschleunigung 4.2.3.1 Theorie zur Beschleunigung Gleichmäßige beschleunigte und bremsende Bewegung Beteiligte physikalische Größen Zeit, Weg, Geschwindigkeit und Kraft 0 Merke Bei der gleichförmig und beschleunigten oder verzögerten Bewegung ändert die Geschwindigkeit fortwährend, nämlich proportional zur Zeit. Unter Beschleunigung bzw. Verzögerung wird die Geschwindigkeitsänderung pro Zeiteinheit verstanden. 0 Aufgabe In den nachfolgenden Grafiken sind die Achsen richtig zu beschriften mit Formelzeichen und Einheiten. Die entsprechende Grafik für den Bewegungsablauf ist einzutragen und mit einem kurzen Satz zu beschreiben. 0 0 Beschleunigung-Zeit-Diagramm 11. Dezember 2013 www.ibn.ch 0 Weg-Zeit-Diagramm Geschwindigkeit-Zeit-Diagramm Version 6 TG 4 2 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE BESCHLEUNIGUNG Beispiel 1 Ist ein Körper bereits in Bewegung, so kann durch eine Krafteinwirkung die Geschwindigkeit verzögert oder verkleinert werden. Seite 19 V Berechnung des Bremsweges: t 0 Die Zeit beim Bremsen soll durch t = v / a ersetzt werden: 11. Dezember 2013 www.ibn.ch Version 6 TG 4 2 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE BESCHLEUNIGUNG Beispiel 2 Ein Körper hat eine Geschwindigkeit von 20 m/s und erfährt ab diesem Zeitpunkt eine Beschleunigung von 2 m/s2 . Seite 20 V Nach welcher Strecke ist die Geschwindigkeit des Körpers verdoppelt? t 0 11. Dezember 2013 www.ibn.ch Version 6 TG 4 2 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE BESCHLEUNIGUNG Beispiel 3 Ein Auto fährt mit einer Geschwindigkeit von 150km / h und beginnt ab diesem Zeitpunkt zu 2 bremsen mit 3 m/s . Seite 21 V Nach welcher Zeit ist die Geschwindigkeit des Autos bei der Hälfte angelangt? Mit welcher Kraft wird der Autofahrer in die Gurten gedrückt. t 0 11. Dezember 2013 www.ibn.ch Version 6 TG 4 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE Seite 22 4.2.4 Horizontaler und schiefer Wurf V Wurfbewegung bzw. beschleunigte Bewegung Beteiligte physikalische Größen Zeit, Weg, Geschwindigkeit und Kraft t 0 11. Dezember 2013 www.ibn.ch Version 6 TG 4 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE 4.2.5 Seite 23 Der freie Fall 4.2.5.1 Theorie zum freien Fall Die Fallbeschleunigung ist gleichförmig beschleunigt und unabhängig vom Gewicht des Körpers. Im Vakuum fallen alle Körper gleich schnell und erfahren die gleiche Fallbeschleunigung. (Bei unseren Betrachtungen werden wir den Luftwiderstand vernachlässigen). Die Fall- oder Erdbeschleunigung wird wie folgt bezeichnet: „g“ kommt von „Galileo Galilei“! V t 0 s t 0 11. Dezember 2013 www.ibn.ch Version 6 TG 4 2 5 TECHNOLOGISCHE GRUNDLAGEN MECHANIK BEWEGUNGSLEHRE DER REIE FALL Seite 24 Aufgabe Eine Münze fällt aus einem Meter auf den Boden. Welche geschwindigkeit hat die Münze beim aufprall auf den Boden. Dabei wird der Luftwiderstand vernachlässigt du die Erdbeschleunigung wird mit 9,81m / s 2 angenommen. V Fallender Körper mit beschleunigter Bewegung. Beteiligte physikalische Größen Zeit, Weg, Geschwindigkeit Kraft t 0 11. Dezember 2013 www.ibn.ch Version 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK Seite 25 4.3 Kräfteberechnung Eine auf einen beweglichen Körper wirkende Kraft kann die-sen in Bewegung setzen; ist der Körper ober schon in Bewegung, so wird sie durch die Kraftwirkung verändert. Ist der Körper nicht beweglich, so wird er durch die Kraft verformt oder deformiert. Kräfte sind vektorielle Grössen. Sie lassen sich durch eine Pfeilstrecke darstellen. Die Länge des Pfeiles entspricht dem Betrag der Kraft unter Berücksichtigung des Massstabes, die Pfeilspitze gibt die Richtung der Kraft auf der Wirkungslinie an. Die Kraft hat die Einheit Newton [N]. Isaac Newton (1643-1727) 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG Seite 26 4.3.1 Kräftedarstellung Im Koordinatensystem kann der Vektor bzw. seine Grösse mit dem Satz von Pythagoras berechnet werden. Der Winkel des Vektors kann mit Hilfe der Trigonometrie berechnet werden. r a r a Vektor Betrag r Der Voktor v Kräfte sind Ursachen für die - Bewegungsänderung von Körpern - Verformung von Körpern 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG 4.3.2 Seite 27 Gewichtskraft 4.3.2.1 Theorie zur Gewichtskraft Jeder Körper besteht aus einem bestimmten Stoff (Material) und hat eine Masse. Diese kann z.B. durch eine Hebelwaage bestimmt werden, d.h. durch Vergleich mit geeichten Gewichtssteinen. Der Wert der Masse ist ortsunabhängig. Die Masseinheit der Masse ist das Kilogramm [kg] Die Dichte eines Stoffes ist definiert als Masse pro Volumeneinheit (Frühere Bezeichnen:Spezifisches Gewicht) Hebelwaage bei Gleichgewicht Die Gewichtskraft eines Körpers ist abhängig von seiner Masse und vom Ort. Sie entsteht durch die Anziehungskraft zweier oder mehrerer Körper. Auf der Erdoberfläche wirkt auf die Masse m = 1 kg eine durchschnittliche Gewichtskraft (Anziehungskraft) von 9,18 N - oder anders ausgedrückt: Ein Körper mit der Masse 1 kg wiegt auf der Erde im Durschnitt 9,81N. Werte für g: 2 - auf der Mondoberfläche 1,67 m/s 2 - auf der Erdoberfläche 9,81 m/ s 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG Seite 28 4.3.3 Kräfteaddition Greifen in einem Punkte mehrere Kräfte an, so kann die resultierende Kraft (Ersatzkraft) durch die vektorielle Addition grafisch oder rechnerisch bestimmt werden. (Sind die Kräfte nicht senkrecht zueinander, so ist für den Praktiker die grafische Lösung vorzuziehen.) Fin Körper ist im Gleichgewicht, wenn die Resultierende aller an ihm angreifenden Kräfte gleich „Null“ ist. (Geschlossenes Kräftepolygon.) Teilkräfte auf gleicher Wirkungslinie und gleicher Richtung Teilkräfte auf gleicher Wirkungslinie und entgegengesetzter Richtung 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG Seite 29 4.3.4 Teilkräfte senkrecht zueinander Teilkräfte senkrecht zueinander 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG Seite 30 4.3.5 Teilkräfte nicht senkrecht zueinander 4.3.5.1 Grafische Lösung Teilkräfte nicht senkrecht 4.3.5.2 Rechnerische Lösung Teilkräfte nicht senkrecht 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG Seite 31 4.3.6 Federkraft Die Federkraft ist proportional zur Federdeformation. Dies ist das berühmte Hooksche Gesetz: x = Federdeformation in [m] D = Federkonstante in [N/m] F = Federkraft in [N] F = D⋅ x Die Federkraft ist der Deformation entgegengerichtet. Sie ist proportional zur Deformation. Als Proportionalitätsfaktor tritt die Federkonstante D auf. Sie ist um so grösser, je stärker die Feder ist. 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG Seite 32 4.3.7 Beschleunigungskraft Um einen Körper bewegen zu können also ist immer eine der Beschleunigung entsprechende notwendig. Diese Kraft muss umso grösser sein, je grösser ist und umso grösser die ist die der Körper erreichen soll. 4.3.7.1 Betrachtungen für die vertikale Bewegung Fällt ein Körper wie bei der Fallbeschleunigung betrachtet herab, so nimmt seine Geschwindigkeit in der Sekunde um 9,81 m/s zu. Die Kraft, die er nach dem Aufprall auf die Unterlage ausübt und die zum Aufheben des Körpers wieder notwendig ist resultiert aus: Diese Gewichtskraft berechnet sich wie folgt: Die Masse eines Körpers ist abhängig von seinem Volumen und der Dichte: 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 7 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRÄFTEBERECHNUNG BESCHLEUNIGUNGSKRAFT 4.3.7.2 Seite 33 Betrachtungen für die horizontale Bewegung Fall 1 Zeichnen Sie in das V-t-Diagramm eine Grafik ein für einen Wagen, der doppelt so schwer und in der halben zeit auf 20m/s Geschwindigkeit beschleunigt wird. V [m/s] 20 m = 0,5t 15 10 5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 t[ °] Berechnungen Was ist zu tun, damit die neue Situation erreicht werden kann? 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 7 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRAFTBERECHNUNG BESCHLEUNIGUNGSKRAFT BETRACHTUNGEN FÜR DIE HORIZONTALE BEWEGUNG Seite 34 Fall 2 Das nebenstehende Diagramm zeigt eine in der Geschwindigkeit gleichbleibende Bewegung. (Also keine Beschleunigung) Frage: Heisst das auch, damit ist keine beschleunigende Kraft mehr notwendig? V m/ s [ ] 20 15 10 5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 t [ ° ] Bemerkungen 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRAFTBERECHNUNG 4.3.8 Seite 35 Spezielle Kräfte 4.3.8.1 Adhäsionskraft Wenn Körper sich enger berühren, so wirken dabei nicht nur Rauhigkeiten der Oberfläche, sondern auch der molekulare Anziehungskräfte verschiedenen Stoffe aufeinander. Diese Anziehungskraft wird auch genannt. Adhäsion Beispiele für diese Wirkung sind: Öl, welches als Flüssigkeit die Reibung vermindert und als Schmiermittel wirkt. Wasser bleibt auf Glasscheibe. Kraft eines Leims und Klebstoffes. Strassenhaftung 4.3.8.2 Kohäsionskraft Die Kohäsionskräfte werden auch mit der Oberflächenspannung in Verbindung gebracht (Zusammenhangskraft). Diese Kräfte bewirken eine Anziehung im gleichen Stoff. In Festen Stoffen sind diese Kräfte am stärksten. In Flüssigkeiten schwächer und in Gasen sehr gering. Beispiele für diese Wirkung sind: Büroklammer schwimmt auf Wasser. Wasserglas ist Randvoll. Gibt dem Wassertropf die typische Tropfenform. Wasser wird zusammengehalten. Eiswürfel im vollen Wasserglas. Insekt läuft auf dem Wasser. Das Wasser läuft aus dem längeren Teil ab, weil eine Kraft (die sogenannte Kohäsionskraft) dafür sorgt, dass das Wasser zusammen bleibt. Die Wasserteilchen im längeren Teil ziehen sozusagen das Wasser aus dem kürzeren Teil hinterher. Zusammenhalt von Wasser 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 8 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRAFTBERECHNUNG SPEZIELLE KRÄFTE 4.3.8.3 Seite 36 Berechnungen zum mechanischen Pendel 11. Dezember 2013 www.ibn.ch Version 6 TG 4 3 8 TECHNOLOGISCHE GRUNDLAGEN MECHANIK KRAFTBERECHNUNG SPEZIELLE KRÄFTE 4.3.8.4 Seite 37 Beweis der Erdrotation Im Jahre 1851 konnte Léon Foucault (1819-68) im Pantheon in Paris zum ersten Mal den experimentellen Beweis für die Erdrotation erbringen. Auch wenn die Erdrotation aus astronomischen Beobachtungen schon klar erschien, so fehlte doch bis dahin ein mechanischer wissenschaftlicher Beweis. Am Nord- bzw. Südpol (90° geogr. Breite) ist der Foucault-Effekt am stärksten - das Pendel schwenkt pro Tag um 360°. Berechnete Ablenkung in unserem Breitengrad: α = ( 360° / 24 ) ⋅ (sin 47° ) = 11° Länge des Seils: 67 m Masse der Kugel: 28 kg 11. Dezember 2013 www.ibn.ch Eigene Bemerkung: Version 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK Seite 4.4 Drehmoment und Seilrollen 4.4.1 Drehmoment 38 Versuch: In allen drei Situationen versucht man einen Hammer zu heben! Situation 1 Gegenkraft F in [N]] Gewichtskraft F in [N]] Situation 2 Gegenkraft F in [N]] Gewichtskraft F in [N]] Situation 3 Gegenkraft F in [N]] Gewichtskraft F in [N]] Beobachtung: Erklärung: 11. Dezember 2013 www.ibn.ch Version 6 TG 4 4 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN DREHMOMENT Seite 39 Es wird sichtbar, dass bei gleichbleibender durch den grösser werdenden eine immer grössere aufgewendet werden muss. Diese Abhängigkeit von bezeichnet man als und . Der „Hebelarm“ ist der senkrechte Abstand vom Drehpunkt zur Wirkungslinie der Kraft. Ist der Winkel nicht 90°, so muss der Hebelarm oder die Kraft grafisch oder rechnerisch entsprechend zerlegt werden! Einseitiger Hebel Winkel zwischen Kraft und Hebelarm 11. Dezember 2013 www.ibn.ch Version 6 TG 4 4 1 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN DREHMOMENT Seite 40 Doppelseitiger Hebel Winkelhebel Träger Bild 8.10.8 Bild 8.10.7 11. Dezember 2013 www.ibn.ch Version 6 TG 4 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN 4.4.2 4.4.2.1 Seite 41 Seilrollen Einfache Seilrolle 11. Dezember 2013 www.ibn.ch Version 6 TG 4 4 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN SEILROLLEN 4.4.2.2 Seite 42 Lose Seilrolle 11. Dezember 2013 www.ibn.ch Version 6 TG 4 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN 4.4.3 Seite 43 Drehmoment auf gleicher Welle Hebel senkrecht Kraft, Drehmoment, Drehzahl und Geschwindigkeit auf der gleichen Welle F1 Merke Kraft ( F ) und Hebelarm ( r ) bzw. Kraft und Abstand zum Drehpunkt ( M ) müssen immer einen rechten Winkel aufweisen. F2 Drehmoment, Mechanische Arbeit [ Nm] F Fraft [N ] r Radius [ m] v Geschwindigkeit [m / s] n Drehzahl [1 / min .] SeilTrommel r1 r2 M M2 M1 MotorWelle Für gilt Kraftübersetzung 11. Dezember 2013 www.ibn.ch Geschwindigkeitsübersetzung Version 6 TG 4 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN 4.4.4 Seite 44 Drehmoment auf ungleicher Welle Hebel senkrecht M Merke Kraft ( F ) und Hebelarm ( r ) bzw. Kraft und Abstand zum Drehpunkt ( M ) müssen immer einen rechten Winkel aufweisen. Kraftübersetzung GeschwindigkeitsDrehzahl- und Zahnradübersetzung Mit Berücksichtigung des Wirkungsgrades Drehmoment, Mechanische Arbeit [ Nm] F Fraft [N ] r Radius [m] v Geschwindigkeit [m / s] n Drehzahl [1 / min .] z Anzahl Zähne [−] ü Übersetzungsverhältnis [−] Wirkungsgrad [−] η F1 [Nm] für SeilTrommel r1 M1 gilt Drehzahlübersetzung F1 Zahnradübersetzung r2 F2 M2 MotorWelle SeilTrommel r1 Geschwindigkeit Siehe 4.2.1 M1 v1 = v2 r2 MotorWelle 11. Dezember 2013 www.ibn.ch M2 F2 Version 6 TG 4 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN 4.5 Die Reibung 4.5.1 Haftreibung Seite 45 Eine Bewegung auf einer Fläche verursacht Reibung. Diese Reibung ist abhängig von der Beschaffenheit der Unterlage auf der die Bewegung erfolgt. Die Haftreibung bzw. die Haftkraft ist jene Kraft, die aufgewendet werden muss bis der Körper zu gleiten beginnt. Die maximale Haftkraft berechnet sich wie folgt: Merke Die Normalkraft FN ist die Kraft die Senkrecht zur Gleitfläche wirkt! In der horizontalen Ebene ist die Normalkraft gleich der Gewichtskraft. 11. Dezember 2013 www.ibn.ch Version 6 TG 4 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN Seite 46 4.5.2 Gleitreibung Die Gleitreibung bzw. die Gleitkraft ist jene Kraft, die aufgewendet werden um den Körper zu bewegen. Die Gleitreibung bzw. die Gleitkraft ist jene Kraft, die aufgewendet werden um den Körper zu bewegen. Die Gleitkraft berechnet sich wie folgt: Merke Die Normalkraft FN ist die Kraft die Senkrecht zur Gleitfläche wirkt! In der horizontalen Ebene ist die Normalkraft gleich der Gewichtskraft. 11. Dezember 2013 www.ibn.ch Version 6 TG 4 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DREHMOMENT UND SEILROLLEN Seite 47 4.5.3 Haftzahl, Gleitreibungszahl und Rollreibungszahl Haften Gleiten Rollen fh f gl fR Stahl 0,15 0,05 0,005 Eiche Eiche parallel zu den Fasern 0,62 0,48 0,54 0,34 Stoffpaar Stahl quer zu den Fasern Holz Stein 0,7 0,3 Schlittschuh Eis 0,03 0,01 Gummi Strasse 0,65 0,3 Riemen Rad 0,7 0,3 Autoreifen Strasse trocken 0,65 0,5 nass 0,4 0,3 Glatteis 0,1 0,05 11. Dezember 2013 www.ibn.ch 0,004 Version 6 TG 4 5 3 TECHNOLOGISCHE GRUNDLAGEN MECHANIK REIBUNG HAFTZAHL, GLEITZAHL UND ROLLREIBUNGSZAHL Seite 48 Beispiel: „Auto“ 11. Dezember 2013 www.ibn.ch Version 6 TG 4 5 TECHNOLOGISCHE GRUNDLAGEN MECHANIK REIBUNG 4.5.4 Seite 49 Reibung auf schiefer Ebene 11. Dezember 2013 www.ibn.ch Version 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK Seite 50 4.6 Druck 4.6.1 Auflagedruck Der Auflagedruck gibt das Druckverhältnis zwischen zwei aufeinandergepressten festen Körpern an, daher wird auch von Pressung oder Flächenpressung gesprochen. A F Bild 8.6.2 Archimedes (285 v. Chr.- 212 v. Chr.) zählt zu den bedeutesten Mathematikern der Menschheit. Er berechnete die Zahl π und bestimmte den Flächeninhalt der Kugel. Wir verdanken ihm die Entdeckung des Hebelgesetzes und die Erforschung des hydrostatischen Auftriebs. Er erfand den Flaschenzug. 4.6.2 Hydraulischer oder Stempelddruck Er wird verursacht durch eine senkrecht wirkende Kraft auf die sogenannte Stempel- oder Kolbenfläche einer Flüssigkeit oder eines Gases. F F1 A1 11. Dezember 2013 www.ibn.ch F2 A1 Version 6 TG 4 6 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DRUCK Seite 51 4.6.3 Auftriebskraft a) Das Volumen eines Tischtenisballes soll bestimmt werden. b) Wie gross ist die Masse des verdrängten Wassers des Versuchsaufbaus? Versuchsaufbau Skizze a) b) Masse des Tischtenisballes mit Wasserfüllung Bestimmung Volumen Tischtenisball 11. Dezember 2013 www.ibn.ch Version 6 TG 4 6 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DRUCK Seite 52 4.6.4 Hydrostatischer Druck oder Gewichtsdruck Beim Schweredruck steht ein Gas oder eine Flüssigkeit unter dem Einfluss der Schwerkraft. A1 A1 p FG1 h1 h2 11. Dezember 2013 www.ibn.ch Version 6 TG 4 6 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK DRUCK HYDROSTATISCHER ODER GEWICHTSDRUCK Seite 53 Beispiel 1 A1 p FG1 11. Dezember 2013 www.ibn.ch h1 Wie gross ist der Druck auf ein U-Boot, das sich 300 m unter der Meeresoberfläche befindet? Version 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK 4.7 Seite 54 Mechanische Arbeit Wird ein Körper (Beispiele: Quader, Wagen) durch eine Kraft über einen bestimmten Weg bewegt, so bezeichnet man den dazu notwendigen physikalischen Aufwand als 4.7.1 Horizontale Bewegung Bewebungskraft F in [N]] 1 11. Dezember 2013 www.ibn.ch 2 Version 6 TG 4 7 TECHNOLOGISCHE GRUNDLAGEN MECHANIK MECHANISCHE ARBEIT Seite 55 4.7.2 Vertikale Bewegung Weitere Formen der mechanischen Arbeit: Bewebungskraft F in [ N]] 2 1 Gewichtskraft F in [ N]] Weitere Formen der mechanischen Arbeit: 11. Dezember 2013 www.ibn.ch Version 6 TG 4 7 TECHNOLOGISCHE GRUNDLAGEN MECHANIK MECHANISCHE ARBEIT Seite 56 4.7.3 Kinetische Energie Berechnungsbeispiel zur kinetischen Energie. Die Daten können der Grafik entnommen werden. Die Angaben sind von den Lernenden an einer Exkursion gesamelt worden. Die „Potentielle“ Energie wird vollständig in „Kinetische“ Energie umgewandelt (ohne Verluste). WK = WP m ⋅ v2 WK = 2 v h = 73 m t Kinetische Energie m = 10 t t =5s Potentielle Energie WP = m ⋅ g ⋅ h Leistung zur Überwindung der potentiellen Energie P= Geschwindigkeit aus der Potentielle Energie v= 2 ⋅ WP m v = 2⋅ g ⋅h WP t Nm s Berechnung 11. Dezember 2013 www.ibn.ch Version 6 TG 4 TECHNOLOGISCHE GRUNDLAGEN MECHANIK Seite 57 4.8 Die mechanische Leistung 4.8.1 Mechanische Leistung Horizontalbewegung Horizonta le zeita bhä ngige Bew egung 1 Bew ebungsk ra ft F in N [ ] 2 James Watt (1736-1819) Bewegung des Wagens Doppelte Zeit bei der Bewegung des Wagens Bemerkung Kraft F [N] Weg s [m] 10 1 10 1 konstant konstant Arbeit W [ Nm ] Zeit t [s] Leistung P [ Nm/s ] Bemerkung 11. Dezember 2013 www.ibn.ch Version 6 TG 4 8 TECHNOLOGISCHE GRUNDLAGEN MECHANIK MECHANISCHE LEISTUNG Seite 58 4.8.2 Mechanische Leistung Wasserturbine Tu rb in e Generator 11. Dezember 2013 www.ibn.ch Version 6 TG 4 8 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK MECHANISCHE LEISTUNG MECHANISCHE LEISTUNG WASSERTURBINE Seite 59 Beispiel: 3 Für ein Wasser-Kraftwerk mit einer Fallhöhe von 25 m und einem Volumenstrom von 40 m pro Sekunde soll die aufgenommene Turbinen-Leistung aus der Grafik herausgelesen werden. 11. Dezember 2013 www.ibn.ch Version 6 TG 4 8 2 TECHNOLOGISCHE GRUNDLAGEN MECHANIK MECHANISCHE LEISTUNG MECHANISCHE LEISTUNG WASSERTURBINE Seite 60 Stauseen der Schweiz Stausee Kanton Lac des Dix Lac d'Émosson Lac de la Gruyère Lac de Mauvoisin Lago di Lei Lago di Livigno Wägitalersee Lac de Joux Lago di Poschiavo Lago di Luzzone Lago di Vogorno Grimselsee Mattmarksee Zervreilasee Sihlsee Limmerensee Lac de Moiry Göscheneralpsee Albignasee Lai da Sontga Maria Schiffenensee Lungerersee Lago del Sambuco Oberaarsee Lai da Marmorera Klöntalersee Lago Ritom Lac de l'Hongrin Lac de Tseuzier Lai da Nalps Lai da Curnera Lac de Salanfe Gigerwaldsee Lago del Narèt Lago dei Cavagnöö Räterichsbodensee Lago di Lucendro Wohlensee Lac de Moron Lac des Toules Lac de Cleuson Griessee Lago Bianco Sufnersee Davosersee Gelmersee Lac du Vieux Lac de Montsalvens Lago Tremorgio Arnensee Engstlensee Stausee Gibidum Bortelsee Wallis Wallis Freiburg Wallis I, Graubünden I, Graubünden Schwyz Waadt Graubünden Tessin Tessin Bern Wallis Graubünden Schwyz Glarus Wallis Uri Graubünden Graubünden Freiburg Obwalden Tessin Bern Graubünden Glarus Tessin Waadt Wallis Graubünden Graubünden Wallis St. Gallen Tessin Tessin Bern Tessin Bern Neuenburg, F Wallis Wallis Wallis Graubünden Graubünden Graubünden Bern Wallis Freiburg Tessin Bern Bern Wallis Wallis 11. Dezember 2013 www.ibn.ch Höhe über Meer 2365 1930 677 1961 1931 1805 900 1005 962 1590 470 1909 2197 1862 889 1857 2249 1792 2163 1908 532 688 1461 2303 1680 848 1850 1255 1777 1908 1956 1925 1335 2310 2310 1767 2134 480 716 1810 2186 2386 2234 1401 1559 1850 2205 801 1830 1543 1850 1436 2464 Inhalt X 10 6 m 3 401 227 220 211 197 165 150 149 111 108 105 103 101 101 97 93 78 76 71 67 66 65 63 61 60 56 54 53 51 45 41 40 36 32 29 27 25 25 21 20 20 19 19 18 15 14 14 13 13 11 11 9 3.6 Name der Talsperre Grande Dixence Émosson Rossens Mauvoisin Valle di Lei Punt dal Gall Schräh Luzzone Contra Seeuferegg Mattmark Zervreila Hühnermatt Limmern Moiry Göscheneralp Albigna Santa Maria Schiffenen Sambuco Oberaar Marmorera Rhodannenberg Piora Hongrin Proz-Riond Nalps Curnera Salanfe Gigerwald Naret Cavagnoli Räterichsboden Lucendro Mühleberg Châtelot Les Toules Cleuson Gries Lago Biango Sufers Gelmer Vieux-Émosson Montsalvens Arnensee Gebidem Bortelsee Mauertyp Gewichtsmauer Bogenmauer Bogenmauer Bogenmauer Bogenmauer Bogenmauer Gewichtsmauer Natursee Natursee Bogenmauer Bogenmauer Gewichtsmauer Erdschüttdamm Bogenmauer Erdschüttdamm Bogenmauer Bogenmauer Steinschüttdamm Gewichtsmauer Bogenmauer Bogenmauer Natursee Bogenmauer Gewichtsmauer Erdschüttdamm Erdschüttdamm Gewichtsmauer Bogenmauer Erdschüttdamm Bogenmauer Bogenmauer Gewichtsmauer Bogenmauer Bogenmauer Bogenmauer Gewichtsmauer Pfeilerkopfmauer Gewichtsmauer Bogenmauer Bogenmauer Gewichtsmauer Gewichtsmauer Gewichtsmauer Bogenmauer Natursee Gewichtsmauer Bogenmauer Bogenmauer Natursee Erdschüttdamm Natursee Bogenmauer Erdschüttdamm Höhe Staumauer 2365 1930 677 1961 1931 1805 900 1005 962 1590 470 1909 2197 1862 889 1857 2249 1792 2163 1908 532 688 1461 2303 1680 848 1850 1255 1777 1908 1956 1925 1335 2310 2310 1767 2134 480 716 1810 2186 2386 2234 1401 1559 1850 2205 801 1830 1543 1850 1436 2464 Version 6 TG 4 8 TECHNOLOGISCHE GRUNDLAGEN MECHANIK MECHANISCHE LEISTUNG Seite 61 4.8.3 Mechanische Leistung aus Drehmoment und Drehzahl 11. Dezember 2013 www.ibn.ch Version 6 TG 4 9 TECHNOLOGISCHE GRUNDLAGEN MECHANIK WIRKUNGSGRAD 4.9 Seite 62 Wirkungsgrad Tu rb in e Generator 11. Dezember 2013 www.ibn.ch Version 6