Aufgabe 1 angelehnt an Schwarze

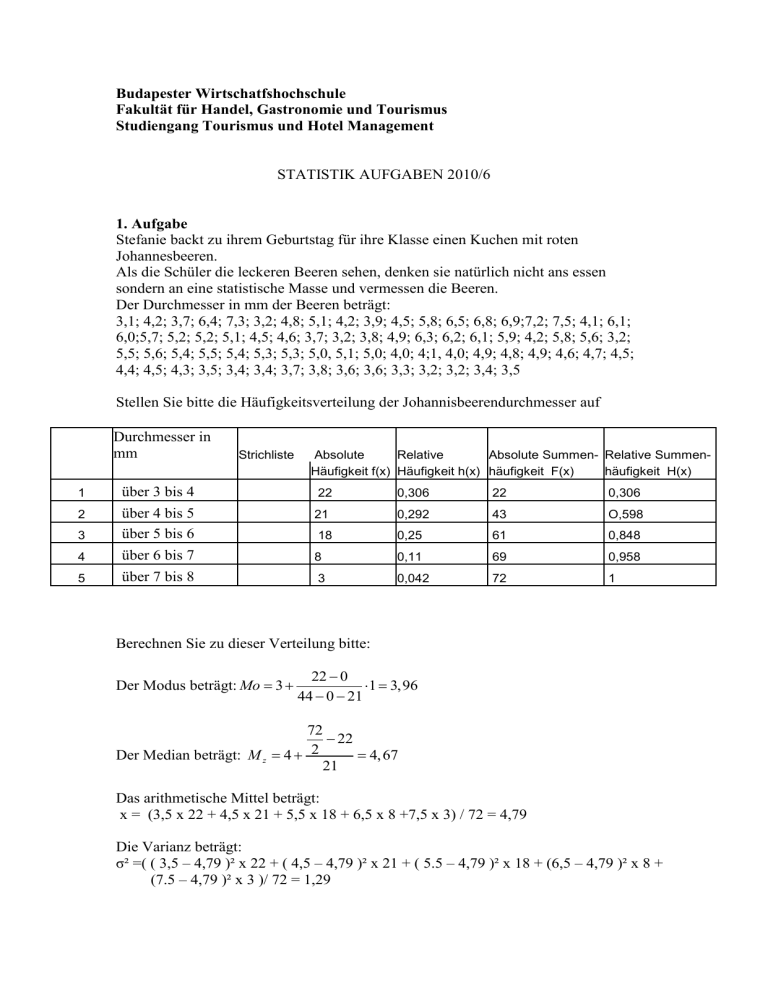
Budapester Wirtschatfshochschule
Fakultät für Handel, Gastronomie und Tourismus
Studiengang Tourismus und Hotel Management
STATISTIK AUFGABEN 2010/6
1. Aufgabe
Stefanie backt zu ihrem Geburtstag für ihre Klasse einen Kuchen mit roten
Johannesbeeren.
Als die Schüler die leckeren Beeren sehen, denken sie natürlich nicht ans essen
sondern an eine statistische Masse und vermessen die Beeren.
Der Durchmesser in mm der Beeren beträgt:
3,1; 4,2; 3,7; 6,4; 7,3; 3,2; 4,8; 5,1; 4,2; 3,9; 4,5; 5,8; 6,5; 6,8; 6,9;7,2; 7,5; 4,1; 6,1;
6,0;5,7; 5,2; 5,2; 5,1; 4,5; 4,6; 3,7; 3,2; 3,8; 4,9; 6,3; 6,2; 6,1; 5,9; 4,2; 5,8; 5,6; 3,2;
5,5; 5,6; 5,4; 5,5; 5,4; 5,3; 5,3; 5,0, 5,1; 5,0; 4,0; 4;1, 4,0; 4,9; 4,8; 4,9; 4,6; 4,7; 4,5;
4,4; 4,5; 4,3; 3,5; 3,4; 3,4; 3,7; 3,8; 3,6; 3,6; 3,3; 3,2; 3,2; 3,4; 3,5
Stellen Sie bitte die Häufigkeitsverteilung der Johannisbeerendurchmesser auf
Durchmesser in
mm
Strichliste
Absolute
Relative
Absolute Summen- Relative SummenHäufigkeit f(x) Häufigkeit h(x) häufigkeit F(x)
häufigkeit H(x)
1
über 3 bis 4
22
0,306
22
0,306
2
21
0,292
43
O,598
3
über 4 bis 5
über 5 bis 6
18
0,25
61
0,848
4
über 6 bis 7
8
0,11
69
0,958
5
über 7 bis 8
3
0,042
72
1
Berechnen Sie zu dieser Verteilung bitte:
Der Modus beträgt: Mo  3 
22  0
1  3,96
44  0  21
72
 22
Der Median beträgt: M z  4  2
 4, 67
21
Das arithmetische Mittel beträgt:
x = (3,5 x 22 + 4,5 x 21 + 5,5 x 18 + 6,5 x 8 +7,5 x 3) / 72 = 4,79
Die Varianz beträgt:
σ² =( ( 3,5 – 4,79 )² x 22 + ( 4,5 – 4,79 )² x 21 + ( 5.5 – 4,79 )² x 18 + (6,5 – 4,79 )² x 8 +
(7.5 – 4,79 )² x 3 )/ 72 = 1,29
Die Standartabweichung beträgt:
σ = √ 1,29 = 1,136
Der Variationskoeffizient beträgt: v = 1,136 / 4,79 = 23,7 %
Das Pearsche Schiefemaß beträgt: (4,79 – 3,96)/ 1,136
22  0
Mo  3 
1  3,96
44  0  21
=
0,73
72
 22
Mz  4 2
 4, 67
21
Aufgabe 2.
Die Ausgaben der Kunden in einem Lebensmittelgeschäft am 3. Juni, 2009 sind in der
folgenden Tabelle dargestellt.
Ausgegebene Summe (in Ft)
bis unter 1000
1000-bis unter 2000
2000-bis unter 3000
3000-bis unter 5000
5000-bis unter 10000
Anzahl der Käufe, 03.06
10
30
91
43
26
Fertigen Sie eine Tabelle an mit den absoluten und relativen Summenhäufigkeiten an
und stellen Sie die aufsteigende und abfallende Summenkurve dar. Geben Sie eine
Schätzung für den Anteil der Käufe, bei denen die Kunden weniger als 2500 Ft / mehr
als 6000 Ft ausgegeben haben.
Untersuchen Sie die Ausgabenkonzentration durch die Lorenzkurve und den GiniKoeffizient!
Ca. 42,5% der Kunden haben für weniger als 2500 Ft eingekauft.
Ca. 10% der Kunden haben für mehr als 6000 Ft eingekauft.
Ausgegebene
Summe in Ft
bis unter 1000
1000-bis unter 2000
2000-bis unter 3000
Klassen
mitte
500
Anzahl relative
kumulierte Gesamt
der
Häufigkeit Häufigkeit umsatz der
Käufe
10
1500
30
2500
91
4000
43
7500
26
3000-bis unter 5000
5000-bis unter 10000
200
Anzahl
u(j)
rel.
rel. Summen- u(j) x (a(j)/v
Häufigkeit
häufigkeit
u(j-1) x (a(j)/v
Klasse a(j) (a(j)/v
0,050
0,050
5.000
0,008
0,008
0,0003879
0
0,150
0,200
45.000
0,070
0,078
0,01396431
0,003491078
0,455
0,655
227.500
0,353
0,431
0,23120636
0,070597362
0,215
0,870
172.000
0,267
0,697
0,23217998
0,174802172
0,130
1,000
195.000
0,303
1,000
0,30256012
0,263227308
0,78029868
0,512117921
1,000
644.500
G=
0,292416602