PN2 Einführung in die Physik für Chemiker 2: Übungsblatt 4

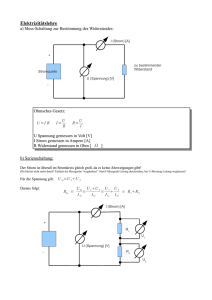
PN2 Einführung in die Physik für Chemiker 2
SS 2017
Übungsblatt 4
Prof. T. Weitz
Übungsblatt 4
Besprechung am 29.05.2017
Aufgabe 1
Ohmsches Gesetz.
a) Ein Lautsprecherkabel aus Kupfer mit einer Länge von 5,0 Metern und einem
Durchmesser von 4,0 Millimetern hat einen Widerstand von 6,76 Milliohm. Berechnen Sie den spezifischen Widerstand von Kupfer.
b) Bei mittlerer Lautstärke hat der angeschlossene Lautsprecher einen Verbrauch
(Leistung) von 50 Watt und er wird mit einer Spannung von 10 Volt betrieben.
Berechnen Sie daraus die Stromstärke. Wie groß ist der Spannungsabfall am Kabel
bei dieser Stromstärke.
c) Um die Klangqualität der Stereoanlage zu verbessern lötet der Besitzer ein zweites
Kabel mit der gleichen Länge und einem Durchmesser von 6 Millimetern parallel an
das erste. Berechnen Sie den Gesamtwiderstand der Kabel in der Parallelschaltung.
Wie hoch ist nun der Spannungsabfall mit obigem Lautsprecher?
Lösung:
a)
2
A
π (2 · 10−3 m)
l
= 1,7 · 10−8 Ωm
R = ρ ←→ ρ = R = 6,76 · 10−3 Ω ·
A
l
5m
b)
I =
P
50 W
=
= 5,0 A
ULS
10 V
UVerlust = R · I = 6,76 · 10−3 Ω · 5 A = 0,034 V
c)
R1 = 6,76 · 10−3 Ω
R2 = ρ
l
5m
= 1,7 · 10−8 Ωm ·
= 3,00 · 10−3 Ω
A
π (3 · 10−3 m)2
1
In einer Parallelschaltung gilt Uges = U1 = U2 = U und Iges = I1 + I2 Einsetzen
des Ohmschen Gesetzes für die Ströme ergibt:
U
U
U
=
+
Rges
R 1 R2
und somit
1
1
1
=
+
Rges
R 1 R2
Rges =
1
R1
1
+
1
R2
=
1
6 76·10−3 Ω
1
+
1
3 00·10−3 Ω
= 2,08 · 10−3 Ω
UVerlust = R · I = 2,00 · 10−3 Ω · 5 A = 0,010 V
Aufgabe 2
Parallel und Reihenschaltung von Widerständen.
Betrachten Sie die folgende Schaltung bestehend aus einer Quelle und 5 Widerständen.
Die Quelle (im Schaltbild links, NG steht für Netzgerät) liefert eine Spannung von
10 Volt. Die Widerstände sind gegeben mit: R1 = 3,3 kΩ, R2 = 6,8 kΩ, R3 = 2,7 kΩ,
R4 = 2,2 kΩ, R5 = 3,9 kΩ.
2
Berechnen Sie den Gesamtwiderstand der Schaltung sowie Spannungsabfall und Strom
für jeden Widerstand. Zeichnen sie außerdem die Stromrichtungen in die Schaltskizze
ein. (Tipp: Es handelt sich hier um eine Parallelschaltung innerhalb einer Parallelschaltung. Berechnen Sie also zunächst den Widerstand der Parallelschaltung aus R1
und R3 mit dem Ergebnis können Sie anschließend den Gesamtwiderstand berechnen.)
Lösung:
Widerstand der kleinen Parallelschaltung:
1
1
1
1
1
=
+
=
+
R1,3
R 1 R3
3,3 kΩ 2,7 kΩ
⇒ R1,3 = 1,485 kΩ
Widerstand der großen Parallelschaltung (Gesamtschaltung):
1
1
1
1
1
=
+
=
+
Rges
R1,3 + R4 + R5 R2
1,485 kΩ + 2,2 kΩ + 3,9 kΩ 6,8 kΩ
⇒ Rges = 3,586 kΩ = 3,6 kΩ
Aufgrund der Regeln für Parallel und Reihenschaltungen gilt für die Spannungen:
UQuelle = U2 = U1 + U5 + U4
U1 = U3 = U1,3
für die Ströme gilt:
I1 + I3 = I1,3 = I4 = I5
Iges = I2 + I4
I2 =
10 V
Uges
= 1,47 mA ≈ 1,5 mA
=
R2
6,8 kΩ
I1 + I3 = I1,3 = I4 = I5 =
Uges
10 V
=
= 1,32 mA ≈ 1,3 mA
R1,3 + R4 + R5
7,585 kΩ
mit U = R · I folgt direkt:
U1,3 = R1,3 · I1,3 = 1,485 kΩ · 1,32 mA = 1,96 V ≈ 2,0 V
U4 = 2,90 V ≈ 2,9 V U5 = 5,15 V ≈ 5,2 V
Check: ergibt zusammenaddiert 10V!(Maschenregel)
U1,3
1,96 V
=
= 0,59 mA
R1
3,3 kΩ
I3 = 0,73 mA
Check: ergibt zusammenaddiert 1,32 mA!(Knotenregel)
I1 =
3
Aufgabe 3
Elektronengeschwindigkeit.
a) In Aufgabe 1b) fließt ein Strom von 5,0 Ampere (A) durch das Lautsprecherkabel. Wie hoch ist die Driftgeschwindigkeit der Leitungselektronen? Kupfer hat
eine Dichte von 8,96 · 103 Kilogramm pro Kubikmeter (kg m−3 ) und eine Molare
Masse von 63,5 Gramm pro Mol (g mol−1 ). Nehmen Sie an, dass jedes Kupferatom ein Leitungselektron zum Stromfluss beiträgt und die Stromdichte über den
Drahtquerschnitt homogen ist.
b) Wie ist es zu erklären, dass das Licht nach Betätigen des Lichtschalters dennoch
nahezu instantan aufleuchtet?
Lösung:
a) Um aus der Stromstärke die Driftgeschwindigkeit der Elektronen zu berechnen
benutzen wir die Formel für die Stromdichte J mit:
J =
I
= n · e · vd ,
A
wobei A die Querschnittsfläche des Kabels, n die Anzahl der Elektronen pro Volumeneinheit, e die Elementarladung und vd die Driftgeschwindigkeit der Elektronen
ist.
Umstellen der Formel nach der Driftgeschwindigkeit ergibt:
vd =
I
.
n ·A·e
Mit der Annahme aus der Aufgabenstellung erhalten wir die Anzahl der Leitungselektronen unter Verwendung der Avogadrokonstante NA , der Dichte von Kupfer
%Cu und der Molaren Masse von Kupfer MCu wie folgt:
n=
1
8,96 · 103 mkg3 · 6 022 · 1023 mol
%Cu · NA
1
=
= 8,49 · 1028 3 .
kg
MCu
m
63,54 · 10−3 mol
Jetzt können wir einsetzen in die Gleichung für die Driftgeschwindigkeit:
vd =
I
I
5,0 A
µm
=
=
= 29,3
1
2
28
−6
2
−19
n ·A·e
n · πr · e
s
8,49 · 10 m3 · 4π · 10 m · 1,6 · 10
C
= 10,5
cm
cm
≈ 11 .
h
h
4
b) Für das Aufleuchten des Lichtes ist nicht die Driftgeschwindigkeit, sondern die Geschwindigkeit mit der sich die Änderung der Driftgeschwindigkeit (wie im Beispiel
des Lichtschalters durch eine angelegtes elektrisches Feld) entlang des Kabels ausbreitet. Diese Geschwindigkeit ist gleich der Lichtgeschwindigkeit, daher leuchtet
die Lampe nahezu gleichzeitig mit Betätigen des Schalters auf.
5